每日一题--删除链表的倒数第 N 个结点

破阵子-晏殊

燕子欲归时节，高楼昨夜西风。

求得人间成小会，试把金尊傍菊丛。歌长粉面红。
斜日更穿帘幕，微凉渐入梧桐。

多少襟情言不尽，写向蛮笺曲调中。此情千万重。

目录

题目描述：

思路分析：

方法及时间复杂度：

法一 双指针(经典解法)

法二 计算链表长度(暴力解法)

法三 栈

法四 哈希表

法五 vector

法六 递归(烧脑解法)

个人总结：

---

 题目描述：

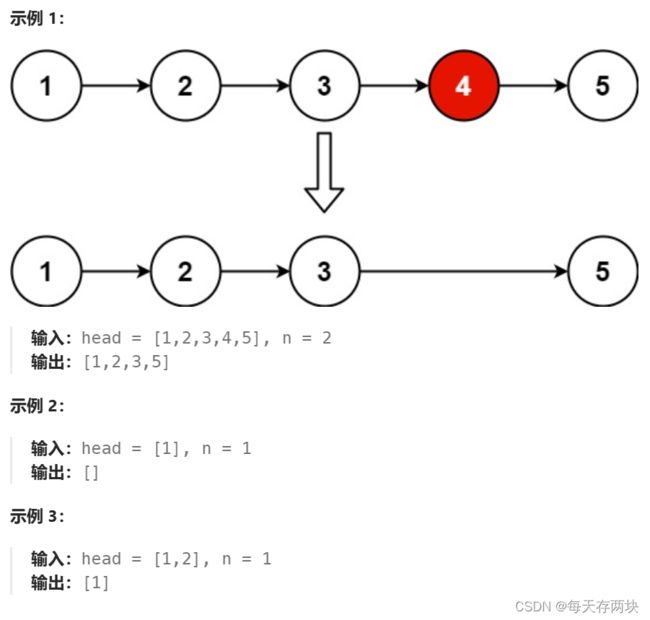
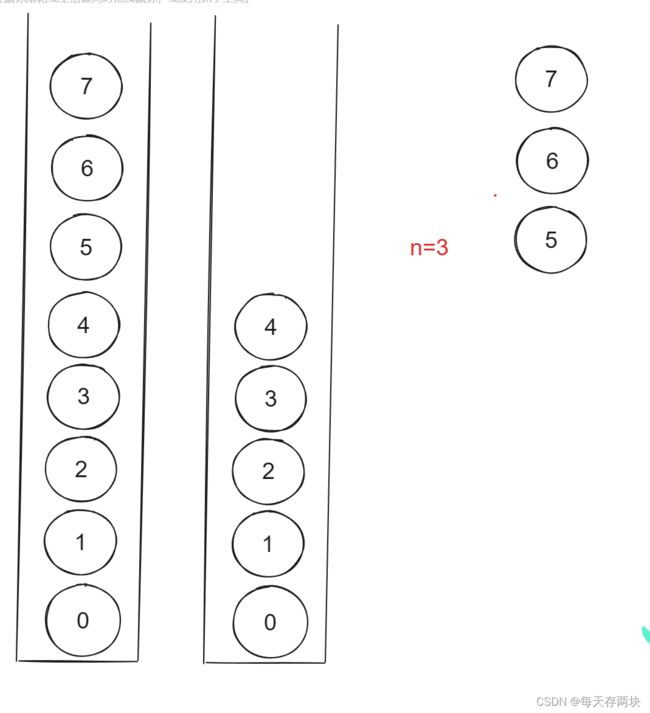
给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

19. 删除链表的倒数第 N 个结点 - 力扣（LeetCode）

思路分析：

此题要求是删除倒数第N个结点，那么主要的就是找到倒数第N个结点，然后让该节点的前一个指向该结点的下一个。

 那么这道题便有五种以上的解法，核心就是找到要删的那个结点。

方法及时间复杂度：

法一 双指针(经典解法)

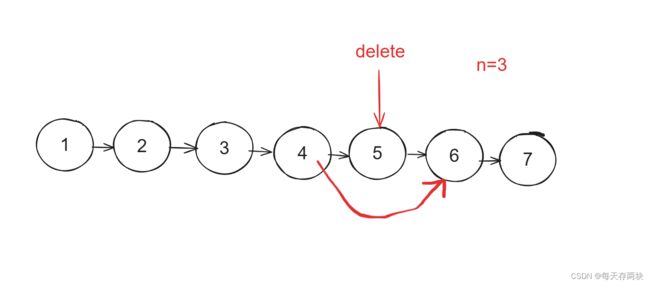
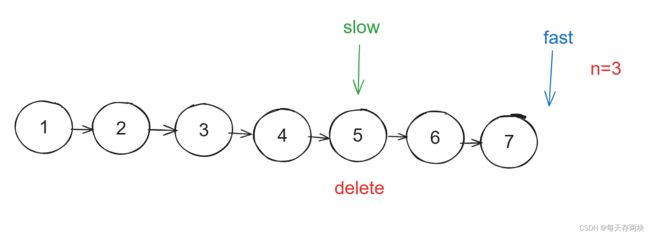
定义两指针：fast=head,slow=head。

fast先走n步，然后fast跟slow同时走。

直到fast走到空，此时slow 就到删除的结点。原理：设链表长L，快指针共走L步，慢指针走L-n步。故此方法由法二得来。

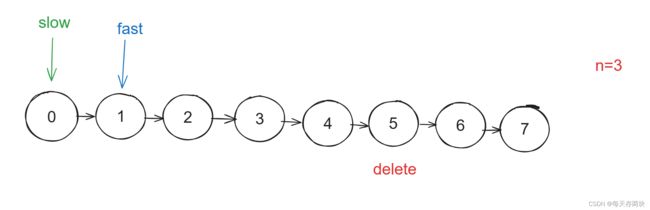
 由于这题是删除该结点，这得需要删除结点的前继结点。所以让slow少走一步。可以直接开辟一个虚拟结点让slow=dummy。

 这样solw就可以到达删除结点的前一个结点了。然后像思路分析那样操作。代码如下：

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummy=new ListNode(0,head);
        ListNode* fast=head,*slow=dummy;
        while(n--){
            fast=fast->next;
        }
        while(fast){
            fast=fast->next;
            slow=slow->next;
        }
        slow->next=slow->next->next;
        ListNode* ans=dummy->next;
        delete dummy;
        return ans;
    }
};

时间复杂度O(L)，链表长度为L。

空间复杂度O(1)。

法二 计算链表长度(暴力解法)

遍历链表计算长度，减去n就是正着数的个数，注意的是，如果长度L-n==0就是头删了。代码如下：

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        int count=0;
        ListNode* cur=head,*pre=head;
        while(cur){
            ++count;
            cur=cur->next;
        }
        if(count==n) return head->next;
        cur=head;
        for(int i=0;i<(count-n)&&cur!=nullptr;++i){
            pre=cur;
            cur=cur->next;
        }
        pre->next=cur->next;
        return head;
    }
};

时间复杂度O(L)，链表长度为L。

空间复杂度O(1)。

法三 栈

根据栈的特点先进后出，创建一个虚拟头节点（防止空栈），让所有结点入栈，然后出栈n个结点，此时栈顶元素就是要删除的结点的前一个。

代码如下：

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummy=new ListNode(0,head);
        stack st;
        ListNode* cur=dummy;
        while(cur){
            st.emplace(cur);
            cur=cur->next;
        }
        for(int i=0;inext=pre->next->next;
        ListNode* ans=dummy->next;
        delete dummy;
        return ans;
    }
};

时间复杂度O(L)，链表长度为L。

空间复杂度O(L)。为栈开销

法四 哈希表

主要思想是一样的，查找到删除结点的前一个结点，如果前一个没有结点就头删。

代码如下：

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        unordered_map hash;
        ListNode *cur=head;
        int i=0;
        while(cur){
            hash.insert({i++,cur});
            cur=cur->next;
        }
        int target=i-n;
        if(target==0) return head->next;
        //target上一个位置的指针指向下一个
        ListNode* left=hash[target-1];
        left->next=left->next->next;
        return head;
    }
};

时间复杂度O(L)，链表长度为L，哈希表查找也为O(L)。

空间复杂度O(L)。哈希表的开销。

法五 vector

与法四思路相同，不多解释。

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        vector ret;
        ListNode* cur=head;
        while(cur){
            ret.emplace_back(cur);
            cur=cur->next;
        }
        int target=ret.size()-n;
        if(target==0) return head->next;
        ListNode* left=ret[target-1];
        left->next=left->next->next;
        return head;
    }
};

时间复杂度O(L)，链表长度为L。

空间复杂度O(L)。

法六 递归(烧脑解法)

这种解法我也受人启发。但使用递归得考虑数据长度，防止栈溢出。思路很简单，与前几种种解法思路相同，定义一个count，递归遍历整个链表，然后回溯整个链表，回溯时count+1。当count==n时，此时已经回溯到要删除结点，此时返回此结点的下一个结点，类似于跳过该结点。

代码如下：

class Solution {
public:
    int count=0;
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        if(!head) return nullptr;
        head->next=removeNthFromEnd(head->next,n);
        count++;
        if(count==n) return head->next;
        return head;
    }
};

时间复杂度O(L)。

空间复杂度O(L)。

个人总结：

大致思路就是找倒数第n个结点，删除结点实现起来其实并不复杂，可以还有更多的方法做这道题。