【深度学习】概率图模型(一)概率图模型理论简介
文章目录
- 一、概率图模型
-
- 1. 联合概率表
- 2. 条件独立性假设
- 3. 三个基本问题
- 二、模型表示
-
- 1. 有向图模型(贝叶斯网络)
- 2. 无向图模型(马尔可夫网络)
- 三、学习
- 四、推断
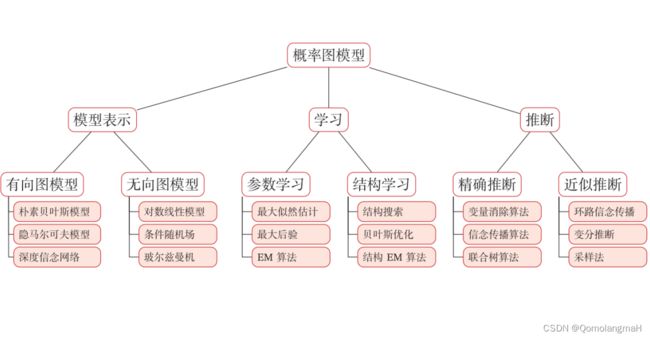
概率图模型(Probabilistic Graphical Model,PGM)是一种用图结构来表示和推断多元随机变量之间条件独立性的概率模型。图模型提供了一种直观且有效的方式来描述高维空间中的概率分布,通过图结构表示随机变量之间的关系,使得模型的参数量得以减少。
一、概率图模型
- 在概率图模型中
- 随机变量通常用斜体的大写字母表示,取值用斜体的小写字母表示。
- 随机向量用粗斜体的大写字母表示,其取值用粗斜体的小写字母表示。
考虑一个由 K K K 个离散随机变量 X 1 , X 2 , … , X K X_1, X_2, \ldots, X_K X1,X2,…,XK 组成的随机向量 X = [ X 1 , X 2 , … , X K ] T \mathbf{X} = [X_1, X_2, \ldots, X_K]^T X=[X1,X2,…,XK]T,其中每个变量都有 M M M 个可能的取值,其联合概率在高维空间中的分布很难直接建模。在没有任何独立性假设的情况下,我们需要为每一种组合分配一个概率值。每个变量有 M M M 个可能的取值,因此有 M K M^K MK 种可能的组合。由于概率的总和必须等于1,所以最后一个概率值可以通过对其他概率值进行补充得到,因此,我们需要 M K − 1 M^K - 1 MK−1 个参数。
当 = 2且 = 100时,参数量(约为 1 0 30 10^{30} 1030)将远远超出目前计算机的存储能力。为了有效减少参数量,可以使用独立性假设。一个维随机向量的联合概率可以分解为个条件概率的乘积。如果某些变量之间存在条件独立性,参数量就可以显著减少。
对于一个 K K K 维随机向量 X \mathbf{X} X,其联合概率可以根据条件独立性假设分解为条件概率的乘积:
p ( x ) ≜ P ( X = x ) = ∏ k = 1 K p ( x k ∣ x 1 , … , x k − 1 ) p(\mathbf{x}) \triangleq P(\mathbf{X} = \mathbf{x}) = \prod_{k=1}^{K} p(x_k | \mathbf{x}_1, \ldots, x_{k-1}) p(x)≜P(X=x)=k=1∏Kp(xk∣x1,…,xk−1)其中, x = [ x 1 , x 2 , … , x K ] \mathbf{x} = [x_1, x_2, \ldots, x_K] x=[x1,x2,…,xK] 表示变量 X \mathbf{X} X 的取值。通过这种分解,我们可以将原本需要 M K M^K MK 个参数的问题,降低到对每个变量的条件概率的参数的数量之和。如果某些变量之间存在条件独立关系,那么相应的条件概率的参数量就可以大幅减少。
概率图模型中,贝叶斯网络和马尔可夫网络都利用了这种条件独立性的结构,以更紧凑的方式表示联合概率分布,从而提高了模型的可解释性和计算效率。
1. 联合概率表
假设有四个二值变量 X 1 , X 2 , X 3 , X 4 X_1, X_2, X_3 , X_4 X1,X2,X3,X4:
- 在不知道这几个变量依赖关系的情况下,可以用一个联合概率表来记录每一种取值的概率,需要 M K − 1 = 2 4 − 1 = 15 M^K − 1 = 2^4 − 1 = 15 MK−1=24−1=15个参数。
- 联合概率表包含了每个可能的组合及其对应的概率。在这个情况下,由于每个二值变量有两个可能的取值,总共有 2 4 = 16 2^4 = 16 24=16种可能的组合。下面是一个简化的例子,其中假设概率分布是均匀的,即 p ( x ) = 1 16 p(\mathbf{x}) = \frac{1}{16} p(x)=161:
X 1 X 2 X 3 X 4 p ( x ) 0 0 0 0 1 16 0 0 0 1 1 16 0 0 1 0 1 16 0 0 1 1 1 16 0 1 0 0 1 16 0 1 0 1 1 16 0 1 1 0 1 16 0 1 1 1 1 16 1 0 0 0 1 16 1 0 0 1 1 16 1 0 1 0 1 16 1 0 1 1 1 16 1 1 0 0 1 16 1 1 0 1 1 16 1 1 1 0 1 16 1 1 1 1 1 16 \begin{array}{cccc|c} X_1 & X_2 & X_3 & X_4 & p(\mathbf{x}) \\ \hline 0 & 0 & 0 & 0 & \frac{1}{16} \\ 0 & 0 & 0 & 1 & \frac{1}{16} \\ 0 & 0 & 1 & 0 & \frac{1}{16} \\ 0 & 0 & 1 & 1 & \frac{1}{16} \\ 0 & 1 & 0 & 0 & \frac{1}{16} \\ 0 & 1 & 0 & 1 & \frac{1}{16} \\ 0 & 1 & 1 & 0 & \frac{1}{16} \\ 0 & 1 & 1 & 1 & \frac{1}{16} \\ 1 & 0 & 0 & 0 & \frac{1}{16} \\ 1 & 0 & 0 & 1 & \frac{1}{16} \\ 1 & 0 & 1 & 0 & \frac{1}{16} \\ 1 & 0 & 1 & 1 & \frac{1}{16} \\ 1 & 1 & 0 & 0 & \frac{1}{16} \\ 1 & 1 & 0 & 1 & \frac{1}{16} \\ 1 & 1 & 1 & 0 & \frac{1}{16} \\ 1 & 1 & 1 & 1 & \frac{1}{16} \\ \end{array} X10000000011111111X20000111100001111X30011001100110011X40101010101010101p(x)161161161161161161161161161161161161161161161161
2. 条件独立性假设
-
联合概率分布:
p ( x 1 , x 2 , x 3 , x 4 ) = p ( x 1 ) ⋅ p ( x 2 ∣ x 1 ) ⋅ p ( x 3 ∣ x 1 , x 2 ) ⋅ p ( x 4 ∣ x 1 , x 2 , x 3 ) p(x_1, x_2, x_3, x_4) = p(x_1) \cdot p(x_2 | x_1) \cdot p(x_3 | x_1, x_2) \cdot p(x_4 | x_1, x_2, x_3) p(x1,x2,x3,x4)=p(x1)⋅p(x2∣x1)⋅p(x3∣x1,x2)⋅p(x4∣x1,x2,x3) -
通过引入条件独立性假设,可以减少参数量:
- 例如,在已知 X 1 X_1 X1时, X 2 X_2 X2和 X 3 X_3 X3独立,即有: p ( x 2 ∣ x 1 , x 3 ) = p ( x 2 ∣ x 1 ) p(x_2|x_1, x_3) = p(x_2|x_1) p(x2∣x1,x3)=p(x2∣x1) p ( x 3 ∣ x 1 , x 2 ) = p ( x 3 ∣ x 1 ) p(x_3|x_1, x_2) = p(x_3|x_1) p(x3∣x1,x2)=p(x3∣x1)
- 在已知 X 2 X_2 X2和 X 3 X_3 X3时, X 4 X_4 X4也和 X 1 X_1 X1独立,即有: p ( x 4 ∣ x 1 , x 2 , x 3 ) = p ( x 4 ∣ x 2 , x 3 ) p(x_4|x_1, x_2, x_3) = p(x_4|x_2, x_3) p(x4∣x1,x2,x3)=p(x4∣x2,x3)
- 这样可以将联合概率分解为四个局部条件概率的乘积,从而减少参数量。 p ( x ) = p ( x 1 ) ⋅ p ( x 2 ∣ x 1 ) ⋅ p ( x 3 ∣ x 1 ) ⋅ p ( x 4 ∣ x 2 , x 3 ) p(\mathbf{x}) = p(x_1) \cdot p(x_2 | x_1) \cdot p(x_3 | x_1) \cdot p(x_4 | x_2, x_3) p(x)=p(x1)⋅p(x2∣x1)⋅p(x3∣x1)⋅p(x4∣x2,x3)
- p ( x 1 ) p(x_1) p(x1) 的参数数量为 1
- M K − 1 = 2 1 − 1 = 1 M^K − 1 = 2^1 − 1 = 1 MK−1=21−1=1
- p ( x 2 ∣ x 1 ) p(x_2 | x_1) p(x2∣x1) 的参数数量为 2(在给定 X 1 X_1 X1 的条件下)
- x 1 x_1 x1有两种情况
- 2 ∗ ( M K − 1 ) = 2 ∗ ( 2 1 − 1 ) = 1 2*(M^K − 1) = 2*(2^1 − 1)= 1 2∗(MK−1)=2∗(21−1)=1
- p ( x 3 ∣ x 1 ) p(x_3 | x_1) p(x3∣x1) 的参数数量为 2(在给定 X 1 X_1 X1 的条件下)
- p ( x 4 ∣ x 2 , x 3 ) p(x_4 | x_2, x_3) p(x4∣x2,x3) 的参数数量为 4(在给定 X 2 X_2 X2 和 X 3 X_3 X3 的条件下)
- x 2 , x 3 x_2, x_3 x2,x3取值有4种情况
- p ( x 1 ) p(x_1) p(x1) 的参数数量为 1
- 总的独立参数数量为 1 + 2 + 2 + 4 = 9 1 + 2 + 2 + 4 = 9 1+2+2+4=9。
3. 三个基本问题
-
表示问题:这个问题涉及如何选择和设计图结构,以有效地表示变量之间的依赖关系。在贝叶斯网络中,这通常涉及到选择合适的有向边,而在马尔可夫网络中,涉及到选择无向边。图结构的选择直接影响了概率模型的表达能力和推断效率。
-
学习问题:学习问题可以进一步分为两个部分:图结构的学习和参数的学习。在图结构的学习中,目标是从数据中推断出最合适的图结构,描述变量之间的依赖关系。在参数的学习中,已知图结构的情况下,目标是估计模型中的参数,使得模型与观测数据的拟合最好。
-
推断问题:推断问题涉及在给定部分变量的观测值时,计算其他变量的条件概率分布。这可以通过贝叶斯推断、变分推断等方法来解决。推断在概率图模型中是一个关键的任务,因为它允许我们根据观测到的证据来推断未观测到的变量的状态,从而进行概率推理。
二、模型表示
概率图模型主要分为两类:有向图模型和无向图模型。
1. 有向图模型(贝叶斯网络)
有向图模型使用有向非循环图(DAG)来描述变量之间的关系。在有向图中,节点表示随机变量,有向边表示因果关系。如果图中有一条从节点 (A) 到节点 (B) 的有向边,表示 (A) 是 (B) 的一个直接因果。在这种模型中,边的方向表示了变量之间的因果关系,而节点之间的有向路径可以表示条件独立性关系。例如,对于三个变量 X 1 , X 2 , X 3 X_1, X_2, X_3 X1,X2,X3,有向图可能是 X 1 → X 2 → X 3 X_1 \rightarrow X_2 \rightarrow X_3 X1→X2→X3,表示 X 1 X_1 X1 影响 X 2 X_2 X2, X 2 X_2 X2 影响 X 3 X_3 X3。
2. 无向图模型(马尔可夫网络)
无向图模型使用无向图来描述变量之间的关系。在无向图中,节点表示随机变量,无向边表示变量之间有概率依赖关系,但不指明因果关系。每一条无向边表示两个变量之间存在概率依赖关系。 例如,对于三个变量 X 1 , X 2 , X 3 X_1, X_2, X_3 X1,X2,X3,无向图可能是 X 1 ∼ X 2 ∼ X 3 X_1 \sim X_2 \sim X_3 X1∼X2∼X3,表示 X 1 X_1 X1 和 X 2 X_2 X2 之间、 X 2 X_2 X2 和 X 3 X_3 X3 之间都存在概率依赖。
三、学习
图模型的学习可以分为两部分:一是网络结构学习,即寻找最优的网络结构;二是网络参数估计,即已知网络结构,估计每个条件概率分布的参数.网络结构学习比较困难,一般是由领域专家来构建.图模型的参数估计问题又分为不包含隐变量时的参数估计问题和包含隐变量时的参数估计问题.
持续更新ing……