体系结构复习（张晨曦 计算机系统结构教程第二版）

体系结构复习（张晨曦 计算机系统结构教程第二版）

第一章

计算机系统的多层级结构

第六级 虚拟机 应用语言机器

↓

第五级 虚拟机 高级语言机器

↓

第四级 虚拟机 汇编语言机器

↓

第三级 虚拟机 操作系统机器

↓

第二级 物理机 传统机器语言机器

↓

第一级 物理机 微程序机器

微程序解释指令系统又称作“仿真”

计算机系统结构经典定义：传统程序员所看到的计算机属性，即概念性结构和功能特性

计算机系统结构广义的定义： 指令系统结构、组成、硬件

计算机组成指的是计算机系统结构的逻辑实现，包含物理机器级中的数据流和控制流的组成以及逻辑设计等。

计算机实现指的是计算机组成的物理实现。

具有相同计算机系统结构的计算机因为速度、价格等方面的要求不同，可以采用不同的计算机组成。而同一种计算机组成又可以采用多种不同的计算机实现，即采用不同的物理结构来实现。

分类法

Flynn分类法

按照指令流和数据流的多倍性进行分类的

指令流：计算机执行的指令序列

数据流：指令调用的数据序列

多倍性：系统最受限的部件上，同时处于同一执行阶段的指令或者数据的最大数目

Flynn分类法把计算机系统的结构分为以下4类

1. 单指令流单数据流
2. 单指令流多数据流
3. 多指令流单数据流
4. 多指令流多数据流

冯氏分类法

用系统的最大并行度对计算机进行分类

最大并行度$P_m$ 定义为：计算机系统在单位时间内能够处理的最大二进制位数

分为4类不同最大并行度的计算机系统结构

n表示字宽，m表示位片宽度，m×n为最大并行度

1. 字串位串 n = 1，m = 1
2. 字并位串 n > 1, m = 1
3. 字串位并 n = 1, m > 1
4. 字并位并 n > 1, m > 1

平均并行度$p_a$

假设每个时钟周期内能够同时处理的二进制位数为$P_i$，则T个时钟周期内的平均并行度为$p_a=\frac{{\sum }_{i=1}^T{P}_i}{T}$

平均利用率$\mu$

系统在T个时钟周期内的平均利用率$\mu =\frac{P_a}{P_m}$

Handler分类法

将计算机硬件结构分为三个层次

1. 程序控制部件（PCU）的个数k
2. 算术逻辑控制部件（ALU）或者处理部件（PE）的个数d
3. 每个算术逻辑部件包含基本逻辑线路（ELC）的套数$\omega$

一个计算机系统的结构用以下公式表示：

$$t(系统型号)=(k,d,\omega )$$

进一步反映流水线的特性，可以将公式改进为

$$t(系统型号)=(k\times k^{{}^{\prime }},d\times d^{{}^{\prime }},\omega \times {\omega }^{{}^{\prime }})$$

Amdahl定律，加速比

$$加速比=\frac{系统性能(改进后)}{系统性能(改进前)}=\frac{总执行时间(改进前)}{总执行时间(改进后)}$$

Fe，可改进比例，可改进部分的执行时间在总的执行时间中所占的比例

Se，加速比（改进部件），改进前的执行时间与改进后的执行时间的比值

改进后的执行时间为

$$T_n=T_0(1-Fe+\frac{Fe}{Se})$$

改进后的加速比为

$$S_n=\frac{T_0}{T_n}=\frac{1}{1-Fe+\frac{Fe}{Se}}$$

CPU性能公式

$$CPU时间=执行程序所需的时钟周期\times 时钟周期时间$$

时钟周期时间是时钟频率的倒数

CPI即每条指令的平均时钟周期数

$$CPI=执行程序所需的时钟周期/所执行的指令条数$$

所以

$$CPU时间=IC\times CPI\times 时钟周期时间$$

所以，CPU的性能取决于

1. 时钟周期时间：取决于硬件实现技术和计算机组成
2. CPI：取决于计算机组成和指令系统的结构
3. IC：指令数量，取决于指令系统的结构和编译技术

$CPU时间=CPU时钟周期数\times 时钟周期时间={\sum }_{i=1}^n(CP{I}_i\times I{C}_i)\times 时钟周期时间$

$$\sum _{i=1}^n(CP{I}_i\times I{C}_i)$$

$CP{I}_i$指的是第i种指令所需要的平均时钟周期数，n为指令的种数，$I{C}_i$为程序执行的过程中第i种指令出现的次数

$CPI=\frac{时钟周期数}{IC}=\frac{{\sum }_{i=1}^n(CP{I}_i\times I{C}_i)}{IC}={\sum }_{i=1}^n(CP{I}_i\times \frac{I{C}_i}{IC})$

程序的局部性原理

局部性包括时间局部性和空间局部性

时间局部性是指程序即将用到的信息很可能就是目前正在使用的信息。

空间局部性是指程序即将用到的信息很可能与目前正在使用的信息在空间上相邻或者很近

利用程序的局部性原理，可以根据程序最近的访问情况来比较准确地预测将要访问的指令和数据。

冯·诺依曼结构

组成

1. 运算器
2. 控制器
3. 存储器
4. 输入设备
5. 输出设备

主要特点

1. 计算器由运算器、存储器、控制器、输入设备、输出设备五大部件组成
2. 指令和数据以同等地位存放于存储器中，并可以按地址访存
3. 指令和数据均使用二进制表示
4. 指令由操作码和地址码组成，操作码用来表示操作的性质，地址码用来表示操作数在存储器中的位置
5. 指令在存储器中按顺序存放，通常是按顺序执行
6. 机器以运算器为中心，输入输出设备和存储器之间的数据传送通过运算器完成

系列机

指的是同一厂家生产的具有相同的系统结构，但是具有不同组成和实现的一系列不同型号的计算机

系列机的软件兼容有四种：

1. 向上兼容

   按某档计算机编制的程序，不加修改就能运行于比它高档的计算机

2. 向下兼容

   按某档计算机编制的程序，不加修改就能运行于比它低档的计算机

3. 向前兼容

   按某个时期投入市场的某种型号计算机编制的程序，不加修改就能运行于在他之前投入市场的计算机

4. 向后兼容

   按某个时期投入市场的某种型号的计算机编制的程序，不加修改就能运行于在他之后投入市场的计算机

目前的计算机只需要保证向上兼容和向后兼容就可以。向后兼容一定要实现，它是系列机的根本特性

仿真和模拟

仿真：用一台现有计算机（称为宿主机）上的微程序去解释实现另一台计算机（称为目标机）的指令系统。

模拟：用软件的方法在一台现有计算机（宿主机）上实现另一台计算机（模拟机）的指令系统

仿真和模拟的主要区别在于解释执行所用的语言：

仿真使用微程序解释执行，解释程序存放在控制存储器中；模拟使用机器语言程序解释执行，模拟程序存储在主存中

仿真的运行速度快

频度的指令使用仿真实现，频度低使用模拟实现

并行

概念

计算机系统在同一时刻或者同一时间间隔内进行多种运算或操作。只要在时间上相互重叠，就存在并行性。并行性包含同时性和并发性两种含义。

同时性：两个或者两个以上的事件在同一时刻发生

并发性：两个或者两个以上的事件在同一时间间隔内发生

并行性的等级

处理数据的角度：

①字串位串<②字串位并<③字并位串<④全并行

①：每次只对一个字的一位进行处理，不存在并行性

②：同时对一个字的全部位进行处理，不同字之间是串行的

③：同时对许多字的同一位进行处理

④：同时对许多字的全部位或者部分位进行处理

执行程序的角度：

Ⅰ指令内部并行<Ⅱ指令级并行<Ⅲ线程级并行<Ⅳ任务级或者过程级并行<Ⅴ作业或者程序级并行

Ⅰ：单条指令中各微操作之间的并行

Ⅱ：并行或者并发地执行两条或者两条以上的指令

Ⅲ：并行执行两个或者两个以上的线程，线程是进程内部一个相对独立、可独立调度和指派的执行单元，但是它基本上不拥有系统资源

Ⅳ：并行执行两个或者两个以上的任务或者过程，以子程序或者进程位调度单元

Ⅴ：并行执行两个或者两个以上的作业或者程序

提高并行性的途径

1. 时间重叠

   流水线技术是时间重叠的典型实例

2. 资源重复

   重复设置硬件资源，大幅度提高计算机系统的性能

3. 资源共享

   软件方法，多个任务按一定的时间顺序轮流使用同一套硬件设备。多道程序、分时系统就是遵循这一途径而产生的。

第二章

指令

指令系统的结构

指令由操作码和地址码构成

CPU中用来存放操作数的存储单元主要有三种：堆栈、累加器、通用寄存器组

指令系统的结构分为堆栈型结构、累加器型结构以及通用寄存器型结构

根据操作数来源不同，通用寄存器结构又可以分为寄存器-存储器型结构RM，寄存器-寄存器型结构RR

RM结构的操作数可以来自存储器，而RR结构的操作数则都是来自通用寄存器组，由于RR结构中只有load指令和store指令能够访问存储器，所以也被称为load-store结构

通用寄存器型结构又可以细分为

1. 寄存器-寄存器型 RR
2. 寄存器-存储器型 RM
3. 存储器-存储器型 MM

控制指令的内容

控制指令是用来改变控制流的

当指令是无条件改变控制流时，称为跳转指令；当控制指令是有条件改变控制流的时候，则称为分支指令

能够改变控制流的指令有4种，分支(brach)、跳转(jump)、过程调用(call)、过程返回(return)

改变控制流的大部分指令是分支指令（条件转移），三种表示分支的方法

1. 条件码
2. 条件寄存器
3. 比较与分支

控制指令中必须给出转移的目标地址，大多数情况下指令中显式地给出目标地址，但是过程返回指令无法显式给出目标地址，因为编译时不知道返回地址

指定转移目标地址最常用的方法是在指令中提供一个偏移量，该偏移量和程序计数器的值相加得到真实的目标地址，这种方式叫做PC相对寻址

  +----+------------------------------+
  |jump|           offset             |    相对跳转指令
  +----+------------------------------+

  (有效PC位址 = 下一條指令的位址 + offset，offset 可為負數) 

PC对寻址的有效地址是下一条指令地址加上偏移参数。 通常对该偏移是有符号数，以允许跳转到指令之前和之后的代码。

这种寻址方式的跳转指令特别有用，因为常见的跳转指令的目标是是附近的指令（在高级语言中，大多数if或while语句相当短）。 实际程序的测量表明，对于大约90％的条件跳转（大约±128或±512字节），8或10位偏移就足够了。

PC相对寻址的另一个优点是代码可以是位置无关的 ，即它可以加载到存储器中的任何地方而无需调整任何地址。

这种寻址模式的某些版本可以是有条件的，这些条件例如两个寄存器之间的关系：“如果reg1 = reg2跳转”、一个寄存器自身：“跳转除非reg1 = 0”或者隐含地状态寄存器中某些位。

指令系统的要求

指令系统的设计包括：指令的功能设计和指令的格式设计

确定哪些基本功能使用硬件实现，考虑因素：速度、成本、灵活性

对指令系统的五个基本要求：完整性、规整性、正交性、高效率性和兼容性

指令操作码的优化

赫夫曼编码

定义：如何用最短的位数表示指令的操作信息和地址信息

赫夫曼编码：

对操作码进行赫夫曼编码，构建赫夫曼树的过程很简单

操作码的优化程度可以用信息熵来衡量：

$$H=-\sum _{i=1}^n{p}_i{\log }_2{p}_i$$

构造的赫夫曼树的平均码长

$$L=\sum _{i=1}^n{p}_i{l}_i$$

信息冗余量

$$R=\frac{L-H}{L}\times 100\%$$

等长拓展码

15/15/15

 +----+----+----+------------+
 |xxxx|xxxx|xxxx|
 +----+----+----+------------+
  
  
 对于15/15/15这种模式来说
 +----+----+----+------------+
 |0000|xxxx|xxxx|
 +----+----+----+------------+
 .
 . 共15条
 .
 +----+----+----+------------+
 |1110|xxxx|xxxx|
 +----+----+----+------------+
 
**************************************

 +----+----+----+------------+
 |1111|0000|xxxx|
 +----+----+----+------------+
 .
 . 共15条
 .
 +----+----+----+------------+
 |1111|1110|xxxx|
 +----+----+----+------------+
 
 **************************************
 
 +----+----+----+------------+
 |1111|1111|0000|
 +----+----+----+------------+
 .
 .共15条
 .
 +----+----+----+------------+
 |1111|1111|1110|
 +----+----+----+------------+
 

8/64/512

 对于8/64/512这种模式来说
 +----+----+----+------------+
 |0000|xxxx|xxxx|
 +----+----+----+------------+
 .
 . 共8条
 .
 +----+----+----+------------+
 |0111|xxxx|xxxx|
 +----+----+----+------------+
 
**************************************

 +----+----+----+------------+
 |1000|0000|xxxx|
 +----+----+----+------------+
 .
 . 共8×8=64条
 .
 +----+----+----+------------+
 |1111|0111|xxxx|
 +----+----+----+------------+
 
 **************************************
 
 +----+----+----+------------+
 |1000|1000|0000|
 +----+----+----+------------+
 .
 .共8×8×8=512条
 .
 +----+----+----+------------+
 |1111|1111|0111|
 +----+----+----+------------+

指令系统的发展方向

CISC方向

复杂指令集 (Complex instruction set computer)

CISC指令系统特点

1. 指令数量多
2. 功能多样

从三个方面对CISC指令系统进行改进

1. 面向目标程序增强指令功能

   提高计算机系统性能最直接的方式，对于使用频度高的指令，用硬件加快其执行；对于使用频度高的指令串，用一条新的指令来代替

   1. 增强运算型指令的功能
   2. 增强数据传送指令的功能
   3. 增强程序控制指令的功能

2. 面向高级语言的优化实现来改进指令系统

   1. 改进指令系统，增加对高级语言和编译器的支持，缩小语义差距，
   2. 对高级语言中使用频度高、执行时间长的语句，应该增强有关指令的功能，加快这些指令的执行速度，或者设置专门的指令
   3. 减少数据传送指令的执行时间
   4. 增强转移指令的功能，增加转移指令的种类
   5. 增强系统结构的规整性，减少系统结构中的各种例外情况

3. 面向操作系统的优化实现改进指令系统

RISC方向

精简指令集 (Reduced instruction set computer)

CISC指令集结构存在的问题：

1. 各种指令的使用频度相差悬殊
2. 指令系统庞大
3. CPI值过大，执行速度慢
4. 指令功能复杂，规整性不好，不利于采用流水技术

RISC原则

1. 指令条数少，指令功能简单
2. 采用简单而又统一的指令格式，并减少寻址方式
3. 指令的执行在单周期内完成
4. 采用load-store结构（即RR结构）
5. 大多数指令使用硬连接逻辑
6. 强调优化编译器的作用，为高级语言程序生成优化代码
7. 充分利用流水技术提高性能

寻址

由寻址方式确定的存储器地址称为有效地址

寻址方式	指令实例	含义
寄存器寻址
立即数寻址
偏移寻址
寄存器间接寻址
索引寻址
直接寻址
寄存器间接寻址
自增寻址
自减寻址
缩放寻址

寻址方式中，物理地址空间的信息存放问题

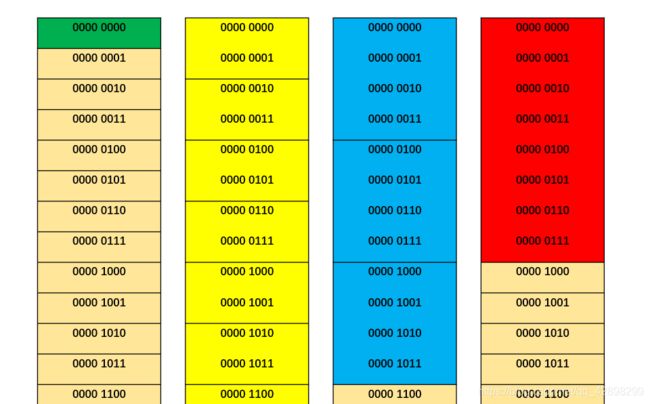
信息宽度不超过主存宽度的信息必须存放在一个存储字中，不能跨界，信息在主存中存放的起始地址必须是该信息宽度（字节数）的整数倍，即

字节信息的起始地址为：x…xxxx

半字信息的起始地址为：x…xxx0

单字信息的起始地址为：x…xx00

双字信息的起始地址为：x…x000

假设主存宽度为8字节，

现在可以理解下面这些话的含义了：

字节信息的起始地址为：x…xxxx

半字信息的起始地址为：x…xxx0

单字信息的起始地址为：x…xx00

双字信息的起始地址为：x…x000

第三章 流水线技术

概念

把一个重复的过程分解成若干个子过程，每个子过程由专门的功能部件来实现。把多个处理过程在时间上错开，依次通过各功能段，这样每个子过程就可以与其他的子过程并行进行。

流水线中的每个子过程及其功能部件陈伟流水段的级或段，流水线的段数称为流水线的深度

流水线技术用于指令的解释过程，形成指令流水线

流水线技术用于运算的执行过程，形成运算操作流水线，

时间最长的段将称为流水线的瓶颈

流水线每一个段后面都要有一个缓冲寄存器，称为流水寄存器。

1. 在两段之间传送数据，以提供后面流水段要用到的信息
2. 隔离各段的处理工作

通过时间、排空时间

通过时间：第一个任务从进入流水线到流出结果所需要的时间

排空时间：最后一个任务从进入流水线到流出结果所需要的时间

流水线的性能指标

吞吐率

单位时间内流水线所完成的任务数量或者输出结果的数量

流水线吞吐率计算：

$$TP=\frac{n}{T_k}$$

n为任务数，$T_k$是处理完n个任务所用的时间，k是一条流水线的段数

各段时间相等

流水线技术的效果就是从通过时间之后，每段时间内都有一个任务结果流出

所以n个任务的执行时间为：

$$T_k=k\times △t+(n-1)\times △t=（k+n-1)△t$$

所以：

$$TP=\frac{n}{(k+n-1)\times △t}$$

$T{P}_{max}={\lim }_{x\to \infty }\frac{n}{(k+n-1)\times △t}=\frac{1}{△t}$

$TP=T{P}_{max}\times \frac{n}{k+n-1}$

当n>>k，即n远大于k时，才有$$TP\approx T{P}_{max}$$

各段时间不完全相等

$T_k={\sum }_{i=1}^k△t_i+(n-1)max(△t_1,△t_2,\cdots ,△t_k)$

$TP=\frac{n}{{\sum }_{i=1}^k△t_i+(n-1)max(△t_1,△t_2,\cdots ,△t_k)}$

$T{P}_{max}=\frac{1}{max(△t_1,△t_2,\cdots ,△t_k)}$

当流水线各段的时间不完全相等的时候，流水线的最大吞吐率和实际吞吐率由时间最长的那个段决定，这就成了整个流水线的瓶颈

消除瓶颈段的方式

1. 细分瓶颈段
2. 重复设置瓶颈段

都能让改进后的流水线吞吐率达到

$T{P}_{max}=\frac{1}{△t}$

加速比

各段时间相等

使用顺序处理方式处理一批任务所用的时间与流水线使用流水处理方式处理同一批任务所用的时间比。

设顺序执行所用的时间为$T_s$，按照流水线方式处理所用的时间为$T_k$，加速比设为S

$S=\frac{T_s}{T_k}$

$T_s=nk△t$

$T_k=k△t+(n-1)△t$

$S=\frac{T_s}{T_k}=\frac{nk}{k+n-1}$

$S_{max}={\lim }_{x\to \infty }S=k$

当n>>k时，流水线的最大加速比等于段数。从这这个意义上来看，段数越多越好

各段时间不等

$S=\frac{T_s}{T_k}=\frac{n{\sum }_{i=1}^k△t_i}{{\sum }_{i=1}^k△t_i+max(△t_1,△t_2,\cdots ,△t_k)}$

效率

流水线设备的利用率，它是指流水线中的设备实际使用时间与整个运行时间的比值

各段时间相等

假设有n个任务，那么每个段被使用的次数应该是n，那么一个段在整个执行过程中实际使用时间为$n△t$

整个执行过程的时间为$T_k$，那么对于各段时间相等的流水线来说，效率

$e=e_1=e_2=e_k=\frac{n△t}{T_k}=\frac{n△t}{(k+n-1)△t}=\frac{n}{k+n-1}$

整条流水线的效率为

$E=\frac{e_1+e_2+\cdots +e_k}{k}=e=\frac{ke}{k}=\frac{kn△t}{k{T}_k}=\frac{n}{k+n-1}$

最高效率为1($n\to \infty$)

$$TP(吞吐量)=\frac{n}{T_k}$$

所以

$E=TP△t$

当流水线各段时间相等的时候，流水线的效率与吞吐量成正比

$S(加速比)=\frac{T_s}{T_k}=\frac{nk}{k+n-1}$

所以

$E=\frac{S}{k}$

流水线的效率是流水线的实际加速比与它的最大加速比k的比值

$E=\frac{kn△t}{k{T}_k}$

从时空图上看，效率就是n个任务占用的时空面积和k段总的时空面积之比

各段时间不等

$E=\frac{n{\sum }_{i=1}^k△t_i}{k[{\sum }_{i=1}^k△t_i+(n-1)\times max(△t_1,△t_2,\cdots ,△t_k)]}$

单功能非线性流水线的最优调度问题

启动距离：一条非线性流水线的输入端连续输入两个任务之间的时间间隔称为非线性流水线的启动距离

禁用启动距离：引起非线性流水线功能段使用冲突的启动距离被称为禁用启动距离

一般都用时钟周期数表示，是正整数

预约表

二维表，横向量表示时间，纵向量表示流水的段。

如果在第n个时钟周期里面使用第k段，则在第k行和第n列的交叉处画一个√

禁止表F

F是禁用启动距离构成的集合

获得方式：

1. 找到预约表的所有√所在位置
2. 所有位置的列号相减取绝对值
3. 将2步所有的结果取并集

初始冲突向量$C_0$

冲突向量$C$是一个N位的二进制位串，

设$C_0=(c_N{c}_{N-1}\cdots c_i\cdots c_2{c}_1)$

KaTeX parse error: No such environment: equation at position 7: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ c_i=\left\{ \b…

$c_i$=1表示不允许间隔i个时钟周期后送入后续任务

状态转换图

初始冲突向量$C_0$决定了下一个任务需要间隔多少时钟周期才可以流入。

设当前冲突向量是$C_k$，j是其中所有允许的时间间隔，则新的冲突向量为KaTeX parse error: Undefined control sequence: \or at position 16: SHR^{(j)}(C_k) \̲o̲r̲ ̲C_0

SHR为逻辑右移，这样处理直到没有新的向量产生

根据状态转换图写出最优调度方案

由初始状态出发，任何一个闭合回路即为一种调度方案

想要找到一种最佳的调度方案，使流水线的吞吐率最高，只要列出所有可能的调度方案，计算出每种方案的平均时间间隔，从中找出最小者即可

五段流水执行过程

1. 取指令周期(IF)

   从存储器中取出指令并放入指令寄存器(IR)，同时PC值4，指向顺序执行的下一条指令

2. 指令译码/读寄存器周期(ID)

   对指令进行译码，并用IR中的寄存器地址去访问通用寄存器组，读出所需的操作数

3. 执行/有效地址计算周期(EX)

   1. load和store指令，ALU将指令中所指定的寄存器的内容与偏移量相加，形成访存有效地址
   2. 寄存器-寄存器ALU指令，ALU按照操作码指定的操作对从通用寄存器中读出的数据进行运算
   3. 寄存器-立即数ALU指令，ALU按照操作码指定的操作对从通用寄存器组中读出的操作数和指令中给出的立即数进行运算
   4. 分支指令，ALU把指令中给出的偏移量与PC值相加，形成转移目标的地址，同时对在前一个周期读出的操作数进行判断，确定分支是否成功

4. 存储器访问/分支完成周期(MEM)

   1. 如果是load指令，则用上个周期获得的有效地址从存储器中读出相应数据；如果是store指令，则把指定的数据写入这个有效地址指定的存储器单元
   2. 分支指令，如果分支成功，则将前一个周期计算出的目标地址送入pc，分支指令完成；否则就不进行任何操作

5. 写回周期(WB)

   1. 对于ALU运算指令来说，这个结果来自ALU，对于load指令来说，这个结果来自存储器
   2. 分支指令和store指令需要4个周期，其他指令需要5个周期

需要解决的问题

1. 保证不会在同一个时钟周期要求同一个功能段作两件不同的工作
2. 避免IF段的访存和MEM段的访存发生冲突
   1. 可以采用分离的指令存储和数据存储
   2. 也可以使用公用的存储器和分离的指令Cache和数据Cache
3. ID要对寄存器进行读操作，WB要对通用寄存器进行写操作，为了防止冲突，将写操作安排在时钟周期的前半拍，读操作安排在后半拍

流水线冲突

相关

定义：两条指令之前存在某种依赖关系。

1. 数据相关

   两条指令i和j，i在j的前面，

   1. j使用i产生的结果
   2. j与指令k数据相关，k与指令i数据相关

2. 名相关

   “名”是指令所访问的寄存器或者存储单元的名称，两条指令使用了相同的名，但是它们之间没有数据流动

   1. 反相关，指令j所写的名与指令i所读的名相同
   2. 输出相关，指令j和指令i所写的名相同，则说它们之间发生了输出相关

   可以使用换名技术消除名相关，即改变指令中操作数的名来消除名相关，对于寄存器操作数进行换名称为”寄存器换名”

3. 控制相关

   分支引起的相关

流水线冲突

1. 结构冲突

   硬件资源满足不了指令重叠执行的要求而发生的冲突

   前一条指令访问存储器时，将流水线停顿一个时钟周期，推迟后面取指令的操作

   或者采用分别设置独立的指令存储器和数据存储器方法

   或者只设置一个存储器，但采用两个分离的cache，指令cache和数据cache

2. 数据冲突

   当指令在流水线中重叠执行的时候，需要用到前面指令的执行结果而发生冲突

   1. 写后读冲突RAW

      使用定向技术解决，将计算结果从产生的地方直接送到其他指令需要它的地方

   2. 写后写冲突WAW，值得注意的是，之前介绍的五段流水是不会产生写后写冲突的，只有

      1. 流水线中不止一个段可以进行写操作
      2. 指令被重新排序了

      这样的流水线中才会出现写后写冲突

   3. 读后写冲突WAR，i读之前，j将新值写入

3. 控制冲突

   流水线遇到分支指令或者其他会改变PC值的指令所引起的冲突

   解决方式

   1. 预测分支失败
   2. 预测分支成功
   3. 延迟分支

第四章 向量处理

1. 横向处理
2. 纵向处理
3. 纵横处理

第七章 存储系统

三级存储系统

Cache，主存储器，磁盘存储器（辅存）构成的三级存储系统

Cache-主存层次，弥补主存速度的不足

主存-辅存层次，弥补主存容量不足，常被用来实现虚拟存储器

两个层次的比较

	Cache-主存层次	主存-辅存层次
目的	为了弥补主存速度的不足	为了弥补主存容量的不足
存储管理的实现	全部由专用硬件实现	主要由软件实现
访问速度的比值（第一级比第二级）	几比一	几万比一
典型的块（页）大小	几十个到几百个字节	几千个以上字节
CPU对第二级的访问方式	可直接访问	均通过第一级
不命中时CPU是否切换	不切换	切换到其他进程

4个问题：

映像规则

查找算法

替换算法

写策略

映像规则

全相联映像

主存中的任何一块都能被放到Cache的任意一个位置

直接映像

主存中，每一个块只能被放置到Cache中唯一的一个位置，

一般情况下，如果主存的第i块映像到Cache块的第j块，则

j = i mod M

M为Cache的块数

设$M=2^m$，则当表示为二进制的时候，j实际上是i的低m位，所以可以直接用主存块的低m位去选择直接映像Cache中的块

组相联映像

主存中的每一块都能映射到唯一的一个Cache分组，但是这个块可以被放入这个分组的任何一个位置。

组的选择使用位选择算法，即对于主存的第i块，若它所映像到Cache的组号为k，则

k = i mod G

G为Cache的组数

设$G=2^g$

同样，可以使用主存块地址的低g位去选择Cahe中的相应组，这里的低g位以及直接映像里面的低m位都被称为索引

如果每个组中有n块，则称该映像为n路组相联，n代表相连度，n越大，Cache的空间利用率就越高，块冲突概率就越低

直接映像的不命中率最高，全相联映像的不命中率最低

替换算法

1. 随机法
2. 先进先出法
3. 最近最少使用法

写策略

写直达法

执行写操作的时候，不仅把数据写到Cache对应的块中，同时也写到下一级存储器

采用写直达法的时候，若进行写操作时，CPU必须等待，直到写操作结束，则称之为“CPU写停顿”，减少写停顿的常用方法是采用写缓冲器

写回法

只把数据写入Cache中相应的块，不写入下一级存储器

这些数据块只有在相应的块被替换时，才被写回下一级存储器

按写分配法：写不命中的时候，先把所写单元所在的块从主存中调入Cache，然后再进行写入

不按写分配法：写不命中时，直接写入下一级存储器而不将相应的块调入Cache

写回法一般采用按写分配法

写直达法一般采用不按写分配法

Cache性能

$平均访存时间=命中时间+不命中率\times 不命中开销$

$CPU时间=(CPU执行周期数+存储停顿周期数)\times 时钟周期时间$

$CPU时间=(IC\times CPI+总访存次数\times 不命中率\times 不命中开销)\times 时钟周期时间$

$=IC\times (CPI+\frac{访存次数}{IC(指令数量)}\times 不命中率\times 不命中开销)$

$=IC\times (CPI+每条指令的平均访存次数\times 不命中率\times 不命中开销)$

一般用CPU时间用来反映存储系统的性能

Cache的不命中率

不命中的类型

1. 强制性不命中

   第一次访问一个块的时候，该块不在Cache中，必须去下一级中调入

2. 容量不命中

   程序执行时所需的块不能全部调入Cache，当某些块被替换时又被重新访问，发生不命中

3. 冲突不命中

   组相联或者直接映像Cache中，太多块映射到同一组中，会出现该组中某个块被别的块替代然后又被重新访问的情况

相联度越高，冲突不命中就越少

强制性不命中和容量不命中不受相联度的影响

强制性不命中不受Cache容量影响，但是容量不命中却随着容量的增加而减少

优化技术

优化技术	不命中率	不命中开销	命中时间	硬件复杂度
1.增加块大小	改进	变差
2.增加Cache容量	改进
3.提高相联度	改进		变差
4.牺牲Cache	改进
5.伪相联Cache	改进
6.硬件预取指令和数据	改进
7.编译技术减少Cache不命中次数	改进
8.读不命中优先于写		改进
9.写缓冲归并		改进
10.尽早重启和关键字优先		改进
11.非阻塞Cache		改进
12.两级Cache		改进
13.小而简单的Cache	变差		改进
14.对Cache进行索引不必进行地址转换			改进
15.流水化Cache访问			改进
16.踪迹Cache			改进
17.编译器控制的预取	改进

多级Cache的不命中率

1. 局部不命中率
2. 全局不命中率

$局部不命中率=\frac{该级Cache的不命中次数}{到达该级Cache的访问次数}$

$全局不命中率=\frac{该级Cache的不命中次数}{CPU发出的访存总次数}$

第二级Cache L2的全局不命中率

$全局不命中{率}_{L2}=不命中{率}_{L1}\times 不命中{率}_{L2}$

$每条指令的平均访存停顿时间=每条指令的平均不命中次{数}_{L1}\times 命中时{间}_{L2}+每条指令的平均不命中次{数}_{L2}\times 不命中开{销}_{L2}$

第八章 输入输出系统

可靠性、可用性、可信性

反映存储外设可靠性的参数

1. 可靠性

   用MTTF，即平均无故障时间，来衡量

   MTTF的倒数是系统的失效率

   系统整体的失效率是各个部件失效率之和

2. 可用性

   平均修复时间MTTR

   衡量系统中断服务的时间

   可用性使用$\frac{MTTF}{MTTF+MTTR}$来衡量

   MTTF + MTTR 可以使平均间隔失效时间MTBF代替

3. 可信性

   无法衡量

RAID

略