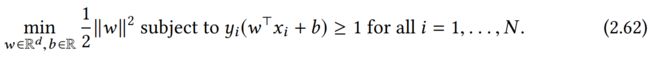【机器学习基础】CH2 - 监督学习(4)支持向量机SVM
2.4 Support Vector Machine 支持向量机
正如我们在核岭回归中所见,尽管 kernel trick 使我们免于显式处理很大甚至无穷大的 feature space dimensions,计算 Gram matrix 时,我们也得计算每对儿点的 k ( x i , x j ) k(x_i,x_j) k(xi,xj)。
如果我们有 N N N 个数据点,相当于每个预测/推断都有 N 2 N^2 N2 个运算。 N N N 很大时,很消耗成本。那么有没有用于计算大量数据的核方法呢?这就是 sparse kernel methods 稀疏核方法,一个例子就是核支持向量机。
2.4.1 线性支持向量机
- Linear (Affine) Functions and Hyperplanes 线性函数和超平面
-
线性函数:
f ( x ) = w x + b ( O n e d i m e n s i o n ) f(x)=wx+b\,\,(One \,\,\, dimension) f(x)=wx+b(Onedimension)f ( x ) = w T x + b ( H i g h e r d i m e n s i o n s ) f(x)=w^Tx+b\,\,(Higher\,\,\,dimensions) f(x)=wTx+b(Higherdimensions)
-
超平面:线性方程的解
2维 → \to → 一条线: w 1 x 1 + w 2 x 2 + b = 0 w_1x_1+w_2x_2+b=0 w1x1+w2x2+b=0
通常情况 → \to → $w^T+b=0 $
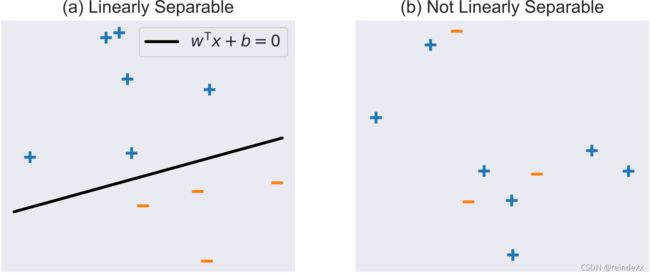
考虑一个二元分类数据集 D = { x i , y i } i = 1 N \mathcal{D}=\{x_i,y_i\}^N_{i=1} D={xi,yi}i=1N,其中每个 x i ∈ R d x_i\in \mathbb{R}^d xi∈Rd 且每个 y i = 1 y_i=1 yi=1 (class +)或 y i = − 1 y_i=-1 yi=−1 (class -)。对于二元分类问题的一个很重要的概念是 linear separability 线性可分性。
-
Definition 2.21: Linear Separability
我们说 D \mathcal{D} D 线性可分,当且仅当存在 w ∈ R d w\in\mathbb{R}^d w∈Rd,使得
w T x i + b > 0 i f y i = + 1 a n d w T x i + b < 0 i f y i = − 1 (2.55) w^Tx_i+b\gt0\,\,if\,\,y_i=+1\,\,and\,\,w^Tx_i+b\lt0\,\,if\,\,y_i=-1\tag{2.55} wTxi+b>0ifyi=+1andwTxi+b<0ifyi=−1(2.55)
对每一个 i = 1 , . . . , N i=1,...,N i=1,...,N。我们现可压缩一下上式(它俩同号):
y i × ( w T x i + b ) > 0 (2.56) y_i\times(w^Tx_i+b)\gt0\tag{2.56} yi×(wTxi+b)>0(2.56)
下面的图像表示了一个线性可分和一个线性不可分的情况,注意到图一的分割线不是唯一的。
-
Margin and Maximum Margin Solution
假定数据集 D \mathcal{D} D 是线性可分。
正如前面所描述的,分割线(或高维的超平面)没有必要一定是惟一的。因此,我们希望找到一个具有理想性质的东西,比如具有良好的 泛化性 。支持向量机通过引入 间隔 / margin 的概念来解决这个问题。
令 w ∈ R d w\in\mathbb{R}^d w∈Rd, b ∈ R b\in\mathbb{R} b∈R,定义一个超平面:
{ x ∈ R d : w T x + b = 0 } (2.57) \{x\in \mathbb{R}^d:w^Tx+b=0\}\tag{2.57} {x∈Rd:wTx+b=0}(2.57)
这个平面也被称为相关决策函数的 __决策边界__ (oracle的近似)。
f ( x ) = { + 1 , w T x + b > 0 − 1 , w T x + b < 0 (2.58) f(x)=\left\{ \begin{aligned} +1,\,\,\,\, w^Tx+b\gt0\\ -1, \,\,\,\, w^Tx+b\lt0 \end{aligned} \right.\tag{2.58} f(x)={+1,wTx+b>0−1,wTx+b<0(2.58)
压缩一下就是:
f ( x ) = S i g n ( w T x + b ) (2.59) f(x)=Sign(w^Tx+b)\tag{2.59} f(x)=Sign(wTx+b)(2.59)
其中 S i g n ( z ) = + 1 Sign(z)=+1 Sign(z)=+1 if z > 0 z\gt0 z>0 且 − 1 -1 −1 if z < 0 z\lt0 z<0。
决策函数的 margin 是数据集 D \mathcal{D} D 中的点到分离超平面 w T + b = 0 w^T+b=0 wT+b=0 的 最小距离 ,其定义为:
m i n i = 1 , . . . , N w T x i + b ∥ w ∥ (2.60) \underset{i=1,...,N}{min} \frac{w^Tx_i+b}{\|w\|}\tag{2.60} i=1,...,Nmin∥w∥wTxi+b(2.60)
1.
这意味着,为了使解能推广,我们就要找到 最大margin解 。margin 越大,我们可容纳的抽样噪声越多 / 提高容错率。而最大margin解可由下面的优化问题得到:
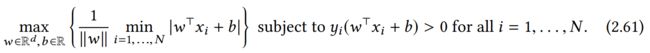
目前,式子(2.61)不是那么容易解决。我们将通过一系列的变换证明这个问题实际上是一个标准约束凸优化问题 a standard constrained convex optimization problem。
-
首先,我们注意到 ∣ w T x i + b ∣ = y i ( w T x i + b ) |w^Tx_i+b|=y_i(w^Tx_i+b) ∣wTxi+b∣=yi(wTxi+b), y i y_i yi 的符号和 w T x i + b w^Tx_i+b wTxi+b 同号且值为1。
-
那么,margin distance y i ( w T x i + b ) / ∥ w ∥ y_i(w^Tx_i+b)/\|w\| yi(wTxi+b)/∥w∥ 对于 w , b w,b w,b是不变的,其中,对于任意 κ > 0 \kappa \gt0 κ>0 , w ↦ κ w w\mapsto \kappa w w↦κw 和 b ↦ κ b b\mapsto \kappa b b↦κb 。
-
因此,不失一般性,我们可以假设,通过取 κ − 1 = m i n i y i ( w T x i + b ) \kappa^{-1}=min_iy_i(w^Tx_i+b) κ−1=miniyi(wTxi+b),对所有 i i i ,有 y i ( w T x i + b ) ≥ 1 y_i(w^Tx_i+b)\ge1 yi(wTxi+b)≥1。
-
那么, m i n i ∣ w T x i + b ∣ = m i n i y i ( w T x i + b ) = 1 min_i|w^Tx_i+b|=min_iy_i(w^Tx_i+b)=1 mini∣wTxi+b∣=miniyi(wTxi+b)=1。对于离决策边界最近的点 x j x_j xj 我们可以得到 y j ( w T x j + b ) = 1 y_j(w^Tx_j+b)=1 yj(wTxj+b)=1。注意,这个点至少是一个,甚至很多。
-
然后,优化问题变为:最大化 1 / ∥ w ∥ 1/\|w\| 1/∥w∥,等价于最小化 ∥ w ∥ 2 / 2 \|w\|^2/2 ∥w∥2/2 (1/2是为了方便求导约了)。
-
总之,式子(2.61)的等价形式为:
优化问题(2.62)是一个有约束的优化问题,求出其解即可求出其最优超平面。利用拉格朗日乘数法对其进行分析是一种有效的方法。 让我们以非正式的方式简要回顾一下。
- 拉格朗日乘数法 Method of Lagrange Multipliers
最小化一个可微函数 F : R m → R F:\mathbb{R}^m \to \mathbb{R} F:Rm→R 的方法一般是令其导数 KaTeX parse error: Undefined control sequence: \grad at position 1: \̲g̲r̲a̲d̲ ̲F = 0。 这就得到了一个驻点 stationary point,然后可以检查它是否确实是一个最小值。
为了达到这个目的,我们可以使用高阶导数 (如,Hessian)或者从函数F的性质推导出极小值。如,如果 F F F 是 convex 凸的,那么任何一个驻点都是(全局)最小值。
我们现考虑约束优化问题,对一些可微约束函数 G : R m → R G:\mathbb{R}^m \to \mathbb{R} G:Rm→R,:
m i n z ∈ R m F ( z ) s u b j e c t t o G ( z ) = 0 (2.63) \underset{z\in \mathbb {R}^m}{min} F(z) \,\,\,\,\,subject \,\,\,\,\,to \,\,\,\,\,G(z)=0\tag{2.63} z∈RmminF(z)subjecttoG(z)=0(2.63)
重要的是,在最佳点 z ^ \hat z z^ 上,∇F和∇G必须是平行的,否则,我们可以沿着曲线 G ( z ) = 0 G(z)=0 G(z)=0 (在局部垂直于∇G),来减少函数 F F F 的值。可被表述为:
∇ F ( z ^ ) + μ ∇ G ( z ^ ) = 0 (2.64) \nabla F(\hat z)+\mu\nabla G(\hat z)=0\tag{2.64} ∇F(z^)+μ∇G(z^)=0(2.64)
其中一部分 μ ≠ 0 \mu\ne0 μ=0。
结合条件 G ( z ^ ) = 0 G(\hat z)=0 G(z^)=0,可得 z ^ \hat z z^ 必须是下式的驻点:
L ( z , μ ) = F ( z ) + μ G ( z ) (2.65) \mathcal{L}(z,\mu)=F(z)+\mu G(z)\tag{2.65} L(z,μ)=F(z)+μG(z)(2.65)
其中 L : R m × R → R \mathcal{L}:\mathbb{R}^m \times \mathbb{R} \to \mathbb{R} L:Rm×R→R 为 Lagrangian 拉格朗日算符, μ \mu μ 为拉格朗日乘子 Lagrange multiplier。
如果我们把等式约束 G ( z ) = 0 G(z)=0 G(z)=0 换成不等式约束 G ( z ) ≤ 0 G(z)\le0 G(z)≤0会怎样?
- 如果 z ^ \hat z z^ 位于约束集的内部,即 G ( z ^ ) < 0 G(\hat z)\lt0 G(z^)<0 ,那么约束是inactive的,所以条件仅仅是 ∇ F ( z ^ ) = 0 \nabla F(\hat z)=0 ∇F(z^)=0。
- 如果 z ^ \hat z z^ 位于约束边界上,即 G ( z ^ ) = 0 G(\hat z)=0 G(z^)=0,那么我们处于前面考虑的等式约束情况
唯一需要注意的是,在不等式的情况下,我们需要∇F和∇G指向不同的方向(见图2.2),否则我们可以移动到约束集的内部,在这个过程中减少F,这与 z ^ \hat z z^的最优性相矛盾。 因此,我们应该使 μ ≥ 0 , μ g ( z ^ ) = 0 \mu\ge 0,\mu g(\hat z)=0 μ≥0,μg(z^)=0 。
一般情况下,我们可能会遇到很多等式约束或不等式约束。但由于等式约束可转换为不等式约束,所以我们仅考虑不等式约束,即: f o r G j ( x ) = 0 我 们 可 以 写 成 G j ( x ) ≤ 0 a n d − G j ( x ) ≤ 0 for \,\,\, G_j(x)= 0\,\,\, 我们可以写成\,\,\,G_j(x)\le 0 \,\, and\,\, -G_j(x)\le 0 forGj(x)=0我们可以写成Gj(x)≤0and−Gj(x)≤0
因此,我们得到下列约束优化问题:
按照前面的方法,我们引入一个拉格朗日乘数向量 μ = ( μ 1 , . . . , μ n ) \mu=(\mu_1,...,\mu_n) μ=(μ1,...,μn),以及拉格朗日算符
然后,按照前面对于单约束情况的方法,我们可以推导出以下必要条件。 这些条件被称为Karush-Kuhn-Tucker (KKT)条件。 在一些称为约束限定的技术假设下,它们可以被证明是优化的必要条件。