密码学—零知识证明（网络空间安全概论）

一、题目描述

1.1题目：

用零知识证明实现地图的三染色问题（用三种颜色染色一个地图，保证任意两个相邻的地区都是不同的颜色）。

编程验证下述的设计思路，采用Python 和 C 语言编写均可。

1.2条件：

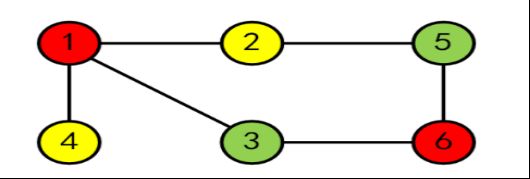
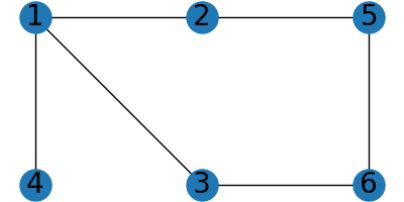
假设一个交互协议有证明者Alice 和验证者 Bob。Alice 手里有一个地图三染色的答案（请见下图），这个图总共有 6 个顶点和 6条边。现在 Alice 想证明给 Bob 她有答案，但是又不想让 Bob 知道这个答案。请用零知识证明的思想设计实验并验证至少20 次的结果。

二、设计思路

2.1实验思路：

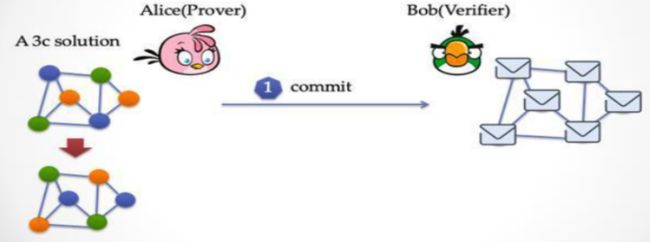
1. Alice 先要对染过色的图进行一些变换，把颜色做一次全改，例如把所有的绿色变成橙色，把所有的黄色变成蓝色，把所有的红色变成粉色。然后 Alice 得到了一个新的染色答案，这时候她把新的图的每一个顶点都用纸片盖上，然后出示给 Bob 看。

2. Bob要随机挑选一条边，并由Alice揭开这条边两端的纸片，让Bob检查，Bob发现这两个顶点的颜色是不同的，那么Bob认为这次检验同构。

经过多次验证，可以证明Bob认为这个图满足三染色的要求。

2.2 编程实现：

本实验采用python作为编程语言，可视化程序采用networksx库构建无向图，通过networkx将生成一个无向图，利用指定节点的边和点坐标来在matplotlib中刻画图案，按照边集数据随机选择相邻的两个点，进行挑战验证，每次颜色随机生成，并选取两点进行验证。判断该边连接的两节点颜色是否一致，重复多次，若多次实验中边的两节点均颜色不同则可判断该图满足三染色要求。

三、运行结果

3.1测试数据：

1） 边集：(1, 2), (1, 4), (1, 3), (2, 5), (3, 6), (5, 6)

颜色集：（1: 0, 2: 1, 3: 2, 4: 1, 5: 2, 6: 0）

3.2运行演示：

程序运行后，会先绘画出原始图形颜色如下图所示

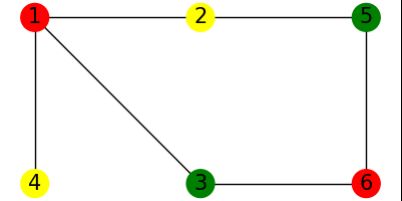
然后关闭该图片后，运行出的图形是更改颜色后的图形，也就是新的染色答案

第三个出现的图片的节点颜色全部相同，实现了上面把每一个顶点都用纸片盖上这一个要求，让用户选择要看哪条边，输入该边的两个结点即可

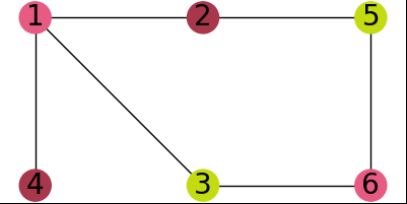
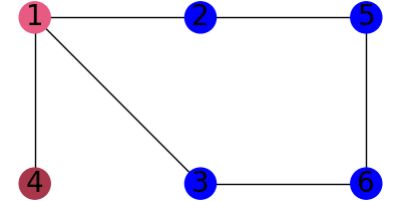
然后出现第四张图片只有用户选择的那两个结点会显示出更改后的颜色，其他结点全部设置为蓝色，以此实现上述揭开这条边两端，让Bob查看这一要求，Bob发现这两个顶点的颜色是不同的，那么Bob认为这次检验同构。

将上述操作进行20次即可。

第一张是Alice拥有的地图三染色答案，第二张图是将颜色全改后得到的图，颜色是随机的，第三张图是将结点全部盖住，让Bob来选择要验证的边，第四张图是Bob选择要验证的边后Alice给看的颜色改后的结点颜色，其他结点用蓝色掩盖。Bob可以看出1，4结点颜色不同，验证正确。然后Bob可进行多次验证。

四、课设总结

零知识证明(zero-knowledge proof)或零知识协议(zero-knowledge protocol)是一种方法，通过该方法，一方（the prover, 证明者）可以向另一方（the verifier, 证明者）证明他们知道值x，而无需传达任何信息，除了他们知道值x。零知识证明的本质是，通过简单地揭示信息来证明某人具有某些信息的知识是微不足道的。面临的挑战是在不透露信息本身或任何其他信息的情况下证明拥有这种财产。零知识证明是打通链上数据与链下计算的关键技术，也是实现链上数据隐私保护的重要途径。所有的证明都体现了证明与验证的不对称性。证明可能是一个非常耗费算力的事情，通过零知识证明，可以尽可能以最小代价实现证明过程。

只要Bob可以不断的进行挑战相应，只要次数N足够大，Alice作弊的概率就会指数级减小，减小到几乎不可能，即可得到命题是否成立。

五、源程序

import random
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
#初始化结点颜色
color0='red'
color1='yellow'
color2='green'
#构造空的无向图
graph= nx.Graph()
#添加结点
node_list = [1,2,3,4,5,6]
for i in range(0,5):
    graph.add_node(node_list[i])
#添加测试数据的边与颜色
edge_list=[(1, 2), (1, 4), (1, 3), (2, 5), (3, 6), (5, 6)]
colors=[color0,color1,color2,color1,color2,color0]

graph.add_edges_from(edge_list)
#画原始图形
plt.rcParams['figure.figsize']= (4, 2)      # 设置画布大小
pos={1: (1.5,2.5), 2: (2.5, 2.5),
3: (2.5, 1.5), 4: (1.5, 1.5),
5: (3.5, 2.5), 6: (3.5, 1.5)}
# pos是布局

nx.draw(graph, pos=pos, with_labels=True, font_size=15, node_size=400, node_color=colors)
plt.show()
#随机生成颜色函数
def randomcolor():
    colorArr = ['1','2','3','4','5','6','7','8','9','A','B','C','D','E','F']
    color = ""
    for i in range(6):
        color += colorArr[random.randint(0,14)]
    return "#"+color
#修改颜色
def changeColor():
    color0=randomcolor()
    color1=randomcolor()
    color2=randomcolor()
    colors = [color0, color1, color2, color1, color2, color0]
    colorchange=colors
    nx.draw(graph, pos=pos, with_labels=True, font_size=20, node_size=500,node_color=colors)
    plt.show()
    nx.draw(graph, pos=pos, with_labels=True, font_size=20, node_size=500)
    plt.show()
    checknode1=int(input("请输入查看的第一个结点"))
    print("颜色是",colors[checknode1-1])
    checknode2=int(input("请输入查看的另一个结点"))
    print("颜色是",colors[checknode2-1])
    m_color = "blue"
    colorchange = [m_color, m_color, m_color, m_color, m_color, m_color]
    colorchange[checknode1-1]=colors[checknode1-1]
    colorchange[checknode2-1] = colors[checknode2-1]
    nx.draw(graph, pos=pos, with_labels=True, font_size=20, node_size=500,node_color=colorchange)
    plt.show()

for i in range(0,1):
    changeColor()