常用数据结构与算法
基本数据结构与算法
数据结构
- 线性表
- 数组
- 链表
- 栈、队列
- 树、二叉树
- 树
- 二叉树
- 二分搜索树
- 平衡二叉树
- 红黑树
- 二叉堆
- 线段树
- Trie
- 集合、映射
- 并查集
算法
- 排序算法
- 二分查找
- DFS、BFS、回溯
- 贪心
- 分治法
- 最短路径
- 字符串匹配
- 动态规划
- 蒙特卡洛
什么是数据结构
数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。
线性表
- 数组的优缺点:
可以直接利用索引进行访问,速度快,在随机访问需求大的时候利用数组来存储数据是不二的选择;但对于一般的编程语言而言,数组的长度是不可变的,这就导致如果对其进行增删操作,我们必须新开辟一个数组,并将原数组的所有元素赋值到新数组相应的位置,是一个相对比较复杂的操作。
- 链表的优缺点:
对于增删操作,链表仅需要改变涉及到的节点的next即可;但对于随机访问而言,由于链表是从头开始访问的,我们对其中的某一个节点进行访问时都需要把它前面的节点访问到,这个过程产生了不必要的时间上的浪费,因此链表是不擅于随机访问的。
- 链表的应用:许多的高级数据结构都用到它,例如Java的HashMap使用链表解决hash冲突,还有经典小游戏“贪吃蛇”
栈与队列
- 栈:后进先出(LIFO),是一种操作受限的线性表,其限制仅允许在表的一端进行插入和删除操作。
- 栈的应用:数制转换、括号匹配、Ctrl+Z操作、Java虚拟机栈…
- 队列:先进先出(FIFO),和栈一样,也是一种操作受限制的线性表,其只允许在表的一端进行插入操作,而在表的另一端进行删除操作。
- 队列的应用:打印机
树
每个节点都有N(N>=0)个子节点,每个节点最多只有 1 个父节点
二叉树
二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。
- 二叉树有不同类型的定义:
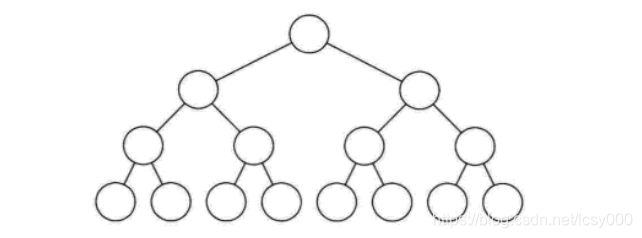
- 完全二叉树:除最底层外树的各层都达到该层的最大数,并且最底层叶子节点都是从左到右依次排布。
- 满二叉树:除叶子节点外每个节点都有左右子节点,并且叶子节点都在树的最底层。
- 平衡二叉树:左右子树的高度差不超过 1 ,且左右子树都是平衡二叉树。
二分搜索树
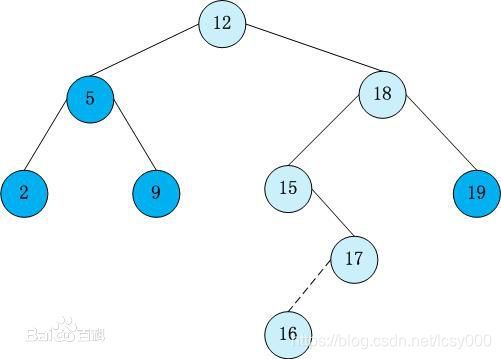
若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。若要处理[12,5,2,18,19,15,17,16,9]这样的数组,则可以将其转化为下图的二分搜索树。
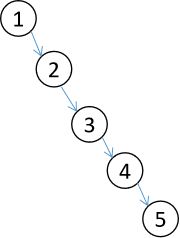
从上图可以很轻易地看出,若需要将这些数据进行排序处理,只需中序遍历二分搜索树即可,其不失为一种排序手段。对于数据的查找则只需依照二分搜索树的定义进行搜索,一般情况下的时间复杂度为O(logN),而在某些特殊情况下,二分搜索树会退化为链表,例如[1,2,3,4,5],如此搜索的时间复杂度则变为O(N)。
平衡二叉树
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
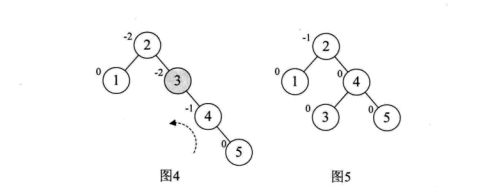
右旋:根是Root,右子树是x,左子树的根为RootL,左子树的两个孩子树分别为LLeftChild和LRightChild。则右旋后,该子树的根为RootL,左子树为LLeftChild,右子树的根为Root,Root的两个孩子树分别为LRightChild(左)和x(右)。
左旋:根是Root,右子树是x,左子树的根为RootL,左子树的两个孩子树分别为LLeftChild和LRightChild。则右旋后,该子树的根为RootL,左子树为LLeftChild,右子树的根为Root,Root的两个孩子树分别为LRightChild(左)和x(右)。
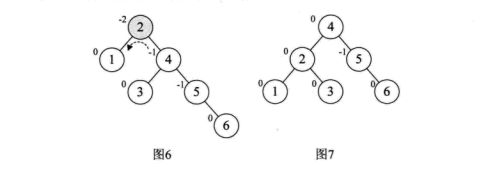
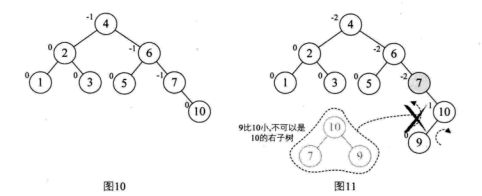
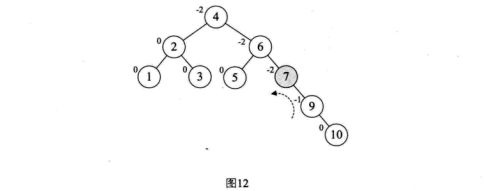
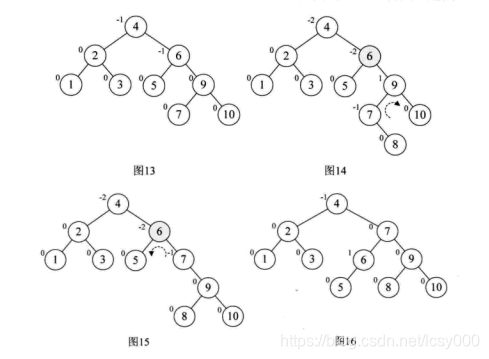
让我们来看看如何实现如下二分搜索树[ 3,2,1,4,5,6,7,10,9,8 ]的转换:
由于平衡二叉树的高度平衡,导致其维护的代价远大于它所带来的收益,故而应用不多。但其搜索性能是优于红黑树的。
红黑树
红黑树和AVL树类似,都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能,它的性质限制决定了它从根到叶子的最长的可能路径不多于最短的可能路径的两倍长,因此它并非高度平衡而只是大致平衡。相比AVL的优点便是对于自身结构性质的恢复操作更加简单。
它虽然是复杂的,但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的: 它可以在O(log n)时间内做查找,插入和删除,这里的n 是树中元素的数目。
红黑树是每个节点都带有颜色属性的二叉查找树,颜色或红色或黑色。在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
- 节点是红色或黑色。
- 根节点是黑色。
- 每个叶节点(NIL节点,空节点)是黑色的。
- 每个红色节点的两个子节点都是黑色