数据结构初阶之二叉树（1）

目录

树的概念和结构

树的概念与结构

树的词汇及概念

树的表示

树的应用场景

二叉树概念和结构

二叉树的概念

二叉树的结构

满二叉树

完全二叉树

 二叉树的特性

二叉树顺序结构及实现

二叉树顺序结构

 二叉树顺序结构的实现(堆)

树的概念和结构

树的概念与结构

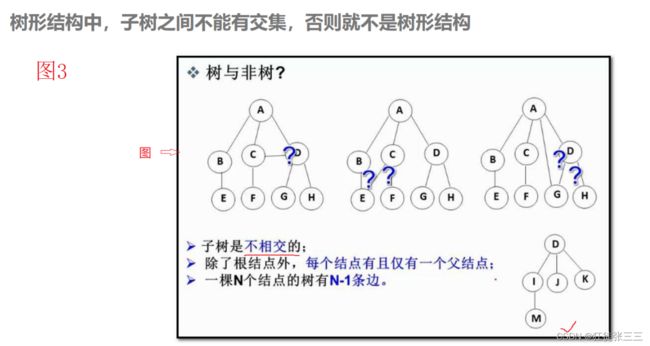
树是一种非线性的结构，是由N（N>=0）个有限节点组成的有层次关系的集合，把它叫做树，是因为它看起来像是一个倒挂的树，也就是说根在上，叶在下的。

树有一个特殊的节点根节点，根节点是没有前驱节点的。

除了根节点以外，其余的节点形成一个M（M>0）个互不相交的集合，每个集合的Ti(1<=i<=M)形成一个类似的子树，每个子树的根节点只有一个前驱，有0或者多个后继节点，因此树是递归定义的。

图1中不同颜色圈起来的部分是子树，子树的根节点有且只有一个前驱节点，有0或者多个后继节点。

图1的子树之间没有交集。

图2中紫色圈内，G节点与H节点相交，此时整个结构已经不是树结构，而是图。

树的词汇及概念

节点的度：一个节点含有子树的个数，成为该节点的度，图4中A节点的度为6。

叶节点或终端节点：度为0的节点称为叶节点，如B、C、H、I........等等。

非终端节点或分支节点：度不为0的节点，A、D、E、F、G......等等。

双亲节点或父节点：若一个节点含有子节点，则该节点称为其子节点的父节点，如A是B的父节点。

孩子节点或子节点：一个节点含有子树的根节点，子树根节点称为该节点的额子节点，如B是A的子节点。

兄弟节点（亲兄弟）：相同父节点的子节点称为兄弟节点，如B、C、D、E、F、G就是兄弟节点。

树的度：一个树结构中，最大的节点的度称为树的度，如图4树的度就是A节点的度为6。

节点的层次：从根开始定义起，根节点为第1层，其子节点为第2层，以此类推。

树的高度或深度：树中节点最大的层次，图4中树的高度为4。

堂兄弟节点：树中在同一层的节点，为堂兄弟节点。

节点的祖先：从根到该节点分支上所经历的所有节点，图4中A是所有节点的祖先。

子孙：以某节点为根的子树中，任意节点都称为该节点的子孙，图4中所有节点都是A的子孙。

森林：由M（M>0）棵不相交的树组成的集合，称为森林。（并查集）

上述红色部分为重要词汇，蓝色部分为次重要词汇。

树的表示

上述已经了解了树的结构，那么树用语言该怎么表示呢，直观的看树可以看成无数个子树的集合，一个节点保存当前的值，同时保存该节点的子节点的地址。

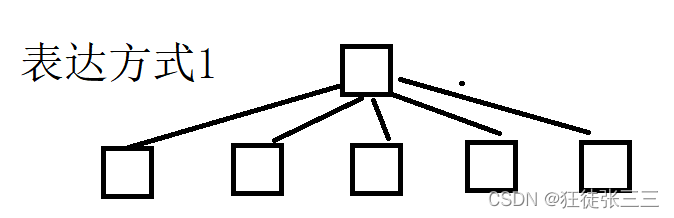
表示方式1：
define N 5
typedef  int TDataType;

typedef struct TNode
{
    TDataType val;
    struct TNode * child[N];
    int childsize;
}

 

 表达方式1中的逻辑结构已经固定了父节点的每个子节点，子节点的数量受到限制，同时子节点数量小于N时，会造成空间浪费。

表示方式2
typedef  int TDataType;

typedef struct TNode
{
    TDataType val;
    struct TNode ** child;
    int childsize;
    int chaildcapacity;
}

 表达方式2比表达方式1实用，可以任意开辟子节点，但是如果子节点过多，会浪费空间。

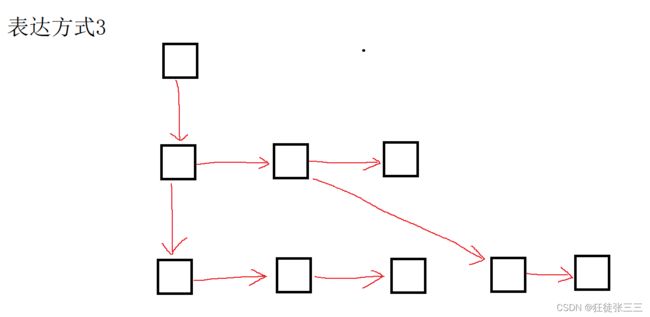
表达方式3

typedef  int TDataType;

typedef struct TNode
{
    TDataType val;
    struct TNode *firstchail;
    struct TNode *nextbrother;
}

 

 表达方式3的树状结构，父节点中只存储一个子节点的地址（第一个子节点），其余的子节点通过第一个子节点中兄弟节点的指针保存，这样的存储方式在逻辑上有些不好理解，但是不浪费空间按需开辟节点。

表达方式3的打印
void printTree(TNode * parent)
{
    assert(parent);
    printf("%d",parent->val);
    TNode *cur=parent->firstchail;
    while(cur)
    {
        printf("%d",cur->val);
        cur=cur->nextbrother;
    }
}

树的应用场景

树作为常见的数据结构，在应用中多作为文件系统使用。

二叉树概念和结构

二叉树的概念

二叉树是树的一种，是一个有限节点的集合，它有几个特点：

1、二叉树可以为空。

2、由一个根节点以及别称左子树和右子树的两颗子树组成。

3、二叉树不存在大于2的度。

4、二叉树的左子树与有子树次序不能颠倒，所以二叉树是有序树。

注意对于二叉树有以下几种情况：

二叉树的结构

满二叉树

二叉树的每层的节点都达到最大值，就是满二叉树

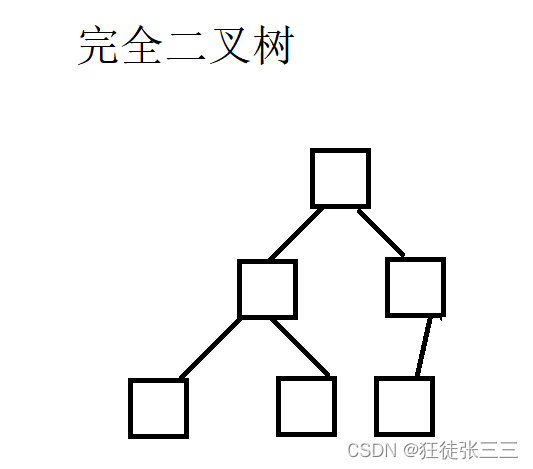
完全二叉树

完全二叉树是由满二叉树而引出来的，若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数(即1~h-1层为一个满二叉树)，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

若一棵二叉树至多只有最下面两层的结点的度数可以小于2，并且最下层的结点都集中在该层最左边的若干位置上，则此二叉树为完全二叉树。
注意：满二叉树是一种特殊的完全二叉树。

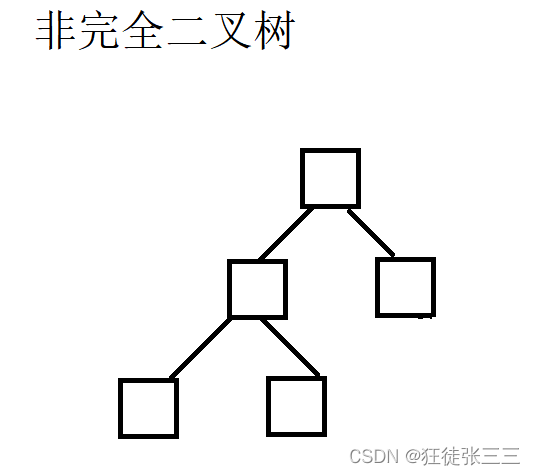
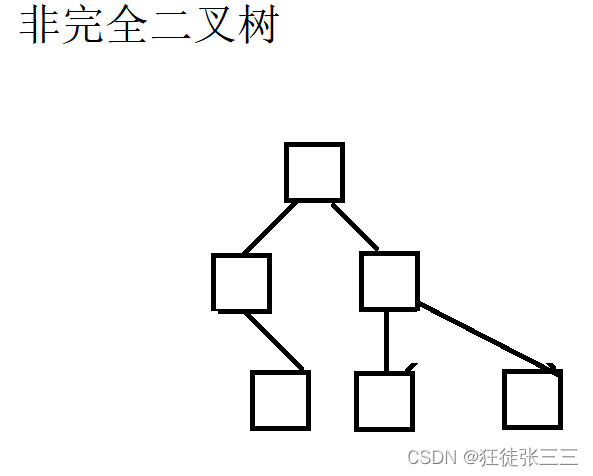
以下的都不是完全二叉树

 

 二叉树的特性

若规定根的层次为1，则一棵非空K层二叉树上，最多有2^k-1个节点（满二叉树），最少有2^(k-1)个节点（2^(k-1)与求除最后一层外其余层次的节点数公式相同）。

若规定根的层次为1，则一个非空K层的二叉树上，每一层的节点个数是2^(K-1)。

对任何以可二叉树，度为0的叶节点个数为n0，度为2的分支节点个数为n2，则有n0=n2+1。

若规定根节点的层数为1，具有n个节点的满二叉树的深度，h=log(n+1)。

 对于具有n个节点的完全二叉树，如果按照从上到下，从左到右的顺序对节点从0开始编号，则对于序号为i的节点有以下几种情况。

当0

当0=0时，无左节点。

当0=0时，无右节点。

二叉树顺序结构及实现

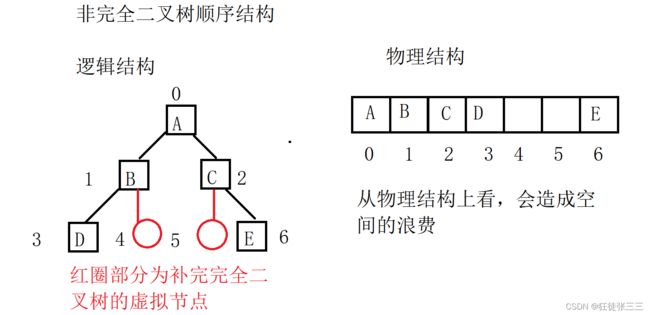
二叉树顺序结构

顺序结构存储就是数组存储，顺序结构存储只适合完全二叉树，如果不是完全二叉树会有空间上的浪费。现实中只有堆才会用数组来存储。

二叉树顺序存储在物理上是数组，在逻辑上是二叉树。

 二叉树顺序结构的实现(堆)

堆分为大堆和小堆，父节点大于子节点的是大堆（大根堆），父节点小于子节点的是小堆（小根堆）。

实现接口：

1、堆的结构：

//1、堆的结构：
typedef int HPDataType;

typedef struct Heap
{
	HPDataType * val;
	int childSize;
	int childCapacity;
}Heap;

2、初始化：

void HeapInit(Heap* php)
{
	assert(php);
	php->val = NULL;
	php->childSize = php->childCapacity = 0;
}

3、插入数据：

//堆的插入数据需要对数据进行调整，如果是最小数，则调整到根节点，大堆反之。
void HeapPush(Heap* php, HPDataType x)
{
	assert(php);
	if (php->childSize == php->childCapacity)
	{
		int newcapacity = php->childCapacity == 0 ? 4 : php->childCapacity * 2;
		int * space = (int *)realloc(php->val,sizeof(HPDataType)*newcapacity);
		php->val = space;
		php->childCapacity = newcapacity;
	}
	php->val[php->childSize] = x;
	int child = php->childSize;
	int parent;
	while (child > 0)
	{
		parent = (child - 1) / 2;
		if (php->val[child] < php->val[parent])
		{
			SwapVal(&php->val[parent], &php->val[child]);
		}
		child = parent;
	}
	php->childSize++;

}

4、删除堆顶元素：

//删除堆顶函数
void HeapPop(Heap* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	SwapVal(&php->val[0], &php->val[php->childSize - 1]);
	php->childSize--;
	int parent = 0;
	int child = 0;
	while (parent < php->childSize)
	{
		if (parent * 2 + 1 < php->childSize)
		{
			child = parent * 2 + 1;
		}
		if (parent * 2 + 2 < php->childSize&&php->val[parent * 2 + 2] < php->val[child])
		{
			child = parent * 2 + 2;
		}
		if (php->val[parent]>php->val[child])
		{
			SwapVal(&php->val[parent], &php->val[child]);
			parent = child;
		}
		else
		{
			break;
		}
	}
}

5、弹出堆顶元素：

//输出堆顶元素
HPDataType HeapTop(Heap* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	return php->val[0];
}

6、判断堆是否为空；

bool HeapEmpty(Heap* php)
{
	assert(php);
	return php->childSize == 0;
}

7、堆的大小；

//堆的大小
int HeapSize(Heap* php)
{
	assert(php);
	return php->childSize;
}

8、堆的打印：

//堆的打印
void HeapPrint(const Heap* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	int i = 0;
	for (i = 0; i < php->childSize; i++)
	{
		printf("%d ", php->val[i]);
	}
	printf("\n");
}