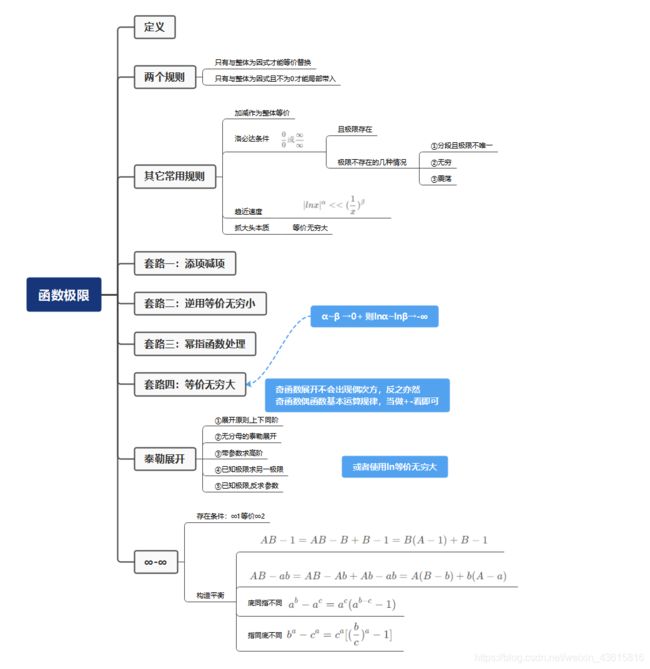
【数学】函数极限计算
目录
- 1.定义
- 2.定理与性质
- 3.做题技巧、题型
-
- 3.1两个游戏规则
- 3.2添项减项,凑出需要的结构
- 3.3逆用等价无穷小
- 3.4见到幂指函数,取指对数
- 3.5幂指函数,几种特殊的处理方式
- 3.6等价无穷大
- 3.7当等价无穷小精度不够,使用泰勒展开
- 3.8无分母的泰勒展开
1.定义
对于任意的 ϵ > 0 \epsilon>0 ϵ>0,存在 δ > 0 \delta>0 δ>0,当 0 < ∣ x − a ∣ < δ 0<|x-a|<\delta 0<∣x−a∣<δ时,有 ∣ f ( x ) − A ∣ < ϵ |f(x)-A|<\epsilon ∣f(x)−A∣<ϵ
称A为 f ( x ) f(x) f(x)当 x → a x→a x→a时的极限,记为 lim x → a f ( x ) = A \lim_{x \to a}f(x)=A x→alimf(x)=A
自己的理解:也就是说,对于任意的一个 ϵ \epsilon ϵ,总能找到一个邻域更接近A(距离小于 ϵ \epsilon ϵ),由此精确刻画极限逼近。
关于定义的易错点与理解
lim x → 0 f ( x ) = A , x 趋 向 但 不 能 等 于 0 \lim_{x \to 0}f(x)=A,x趋向但不能等于0 x→0limf(x)=A,x趋向但不能等于0
一 个 函 数 要 在 x 0 点 有 极 限 , 在 x 0 可 以 无 定 义 , 但 在 x 0 的 去 心 领 域 要 有 定 义 一个函数要在x_0点有极限,在x_0可以无定义,但在x_0的去心领域要有定义 一个函数要在x0点有极限,在x0可以无定义,但在x0的去心领域要有定义
2.定理与性质
①唯一性
②局部有界性
③局部保号性
④运算规则
⑤夹逼准则
⑥洛必达法则
⑦泰勒公式
保号性是指极限的保号性属于极限一种性质,函数极限都是在邻域里面定义的,所以对应所得函数性态也是在邻域里。数列极限是当n大于N时也就是N以后的项具有保号性。
3.做题技巧、题型
需熟记 泰勒展开表、等价替换 传送门(点我)
3.1两个游戏规则
①泰勒展开时注意精确度,等价替换时需是因子(与其余整体构成乘除关系)才可替换(其本质还是精确度)。
②局部代入的条件:非零因子(与其余整体构成乘除关系)
3.2添项减项,凑出需要的结构
通过(AB-1)制造出 (A-1)和 (B-1)
A B − 1 = A B − B + B − 1 = B ( A − 1 ) + ( B − 1 ) AB-1 =AB-B+B-1=B(A-1)+(B-1) AB−1=AB−B+B−1=B(A−1)+(B−1)

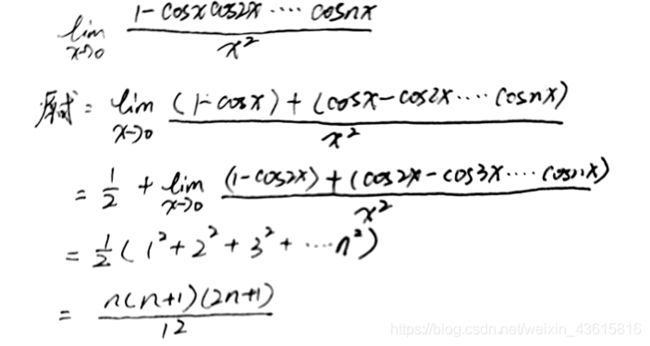
3.3逆用等价无穷小
当 x → 0 x \to0 x→0时, x x x~ l n ( 1 + x ) ln(1+x) ln(1+x)
当 x → 1 x \to1 x→1时, x − 1 x-1 x−1~ l n x lnx lnx
这种方法一般是先逆用一次,把极限拆开后,再顺用一次,特别适合和用于含有" A 1 A 2 A 3 . . . A n − 1 A_1A_2A_3...A_n-1 A1A2A3...An−1"的结构式子
有了这个技巧,可秒杀上面两题
把 ( 1 + α x ) m ⋅ ( 1 + β x ) n \sqrt[m]{(1+\alpha x)}·\sqrt[n]{(1+\beta x)} m(1+αx)⋅n(1+βx) 看做一个整体x,则这个整体趋向于1


3.4见到幂指函数,取指对数
幂指函数是指形如: x x x^x xx
取指对数是指: a b = e l n a b = e b l n a a^b=e^{lna^b}=e^{blna} ab=elnab=eblna
由于当 x → 1 , x \to 1, x→1, l n x = l n ( ( x − 1 ) + 1 ) lnx=ln((x-1)+1) lnx=ln((x−1)+1)~ x − 1 x-1 x−1
所以可得
对 于 1 ∞ 类 型 的 重 要 极 限 : v ( x ) u ( x ) = e l n v ( x ) u ( x ) = e u ( x ) l n v ( x ) 对于1^\infty类型的重要极限:v(x)^{u(x)}=e^{lnv(x)^{u(x)}}=e^{u(x)lnv(x)} 对于1∞类型的重要极限:v(x)u(x)=elnv(x)u(x)=eu(x)lnv(x)
又因为当 x → 1 , x \to 1, x→1, l n x = l n ( ( x − 1 ) + 1 ) lnx=ln((x-1)+1) lnx=ln((x−1)+1)~ x − 1 x-1 x−1
所以得
对 于 1 ∞ 类 型 的 重 要 极 限 可 一 步 到 位 : v ( x ) u ( x ) = e u ( x ) ( v ( x ) − 1 ) 对于1^\infty类型的重要极限可一步到位:v(x)^{u(x)}=e^{u(x)(v(x)-1)} 对于1∞类型的重要极限可一步到位:v(x)u(x)=eu(x)(v(x)−1)
3.5幂指函数,几种特殊的处理方式
- 巧用无穷小吸收律,打败纸老虎(看起来很复杂,实则很简单)

- 几种特殊的形式
当出现这几种幂指函数时
a b − c d ( 较 难 算 ) a^b-c^d (较难算) ab−cd(较难算)
a b − a c = a c ( a b − c − 1 ) a^b-a^c = a^c(a^{b-c}-1) ab−ac=ac(ab−c−1)
a c − b c = b c [ ( a c ) c − 1 ] a^c-b^c=b^c[(\frac{a}{c})^c-1] ac−bc=bc[(ca)c−1]
有了这些技巧,可尝试此题
lim x → 0 ( 3 + 2 t a n x ) x − 3 x 3 s i n 2 x + x 3 c o s 1 x \lim_{x \to 0} \frac{(3+2tanx)^x-3^x}{3sin^2x+x^3cos\frac{1}{x}} x→0lim3sin2x+x3cosx1(3+2tanx)x−3x
ps:此题用到的技巧 无穷小吸收律+逆用等价无穷小+正用等价无穷小

大学生数学竞赛中填空题最后一题
设 f ( x ) 、 g ( x ) 在 x = 0 的 领 域 U 内 有 定 义 , 且 对 ∀ x ∈ U , 均 有 f ( x ) ≠ g ( x ) , 且 lim x → 0 f ( x ) = lim x → 0 g ( x ) = a > 0 , 设f(x)、g(x)在x=0的领域U内有定义,且对\forall x \in U, 均有f(x) \ne g(x),且 \lim_{x \to 0}f(x)= \lim_{x \to 0}g(x)=a>0, 设f(x)、g(x)在x=0的领域U内有定义,且对∀x∈U,均有f(x)=g(x),且x→0limf(x)=x→0limg(x)=a>0,
则 lim x → 0 [ f ( x ) ] g ( x ) − [ g ( x ) ] g ( x ) f ( x ) − g ( x ) = ? 则 \lim_{x \to 0}{\frac{[f(x)]^{g(x)}-{[g(x)]^{g(x)}}}{f(x)-g(x)} } =? 则x→0limf(x)−g(x)[f(x)]g(x)−[g(x)]g(x)=?

3.6等价无穷大
首先需熟记 泰勒展开表、等价替换 传送门(点我)
同时需记住这个结论:对数函数增长慢,可用洛必达法则检验,不过为了速度,最好记住结论
lim x → + ∞ l n x x = 0 , 对 数 函 数 增 长 慢 , 对 数 函 数 是 垃 圾 \lim_{x\to+\infty}{\frac{lnx}{x}}=0 ,对数函数增长慢,对数函数是垃圾 x→+∞limxlnx=0,对数函数增长慢,对数函数是垃圾
而 考 试 通 常 喜 欢 变 形 , lim g ( x ) → + ∞ l n g ( x ) g ( x ) = 0 而考试通常喜欢变形,\lim_{g(x)\to+\infty}{\frac{lng(x)}{g(x)}}=0 而考试通常喜欢变形,g(x)→+∞limg(x)lng(x)=0
另外还要知道这个结论
若 α ~ β → 0 + , 则 l n α ~ l n β → − ∞ 若 α~\beta \to 0^+,则 ln \alpha ~ln \beta \to -\infty 若α~β→0+,则lnα~lnβ→−∞
结论简单证明
lim l n α l n β − 1 = l n α β l n β = 0 所 以 可 得 l i m l n α l n β = 1 \lim {\frac{ln\alpha}{ln\beta}}-1=\frac{ln{\frac{\alpha}{\beta}}}{ln\beta}=0所以可得 lim\frac{ln \alpha}{ln \beta}=1 limlnβlnα−1=lnβlnβα=0所以可得limlnβlnα=1
此结论来自于 李正元老师的复习全书
巧用等价无穷大,可尝试下题
题 目 : lim x → 0 + ( e x − 1 − x ) 1 l n x 题目:\lim_{x\to0^+}(e^x-1-x)^{\frac{1}{lnx}} 题目:x→0+lim(ex−1−x)lnx1
解的过程如下
取 指 对 数 : 原 式 = lim x → 0 + e 1 l n x l n ( e x − 1 − x ) 取指对数:原式=\lim_{x\to0^+}e^{\frac{1}{lnx}ln(e^x-1-x)} 取指对数:原式=x→0+limelnx1ln(ex−1−x)
又 ∵ 若 α ~ β → 0 + , 则 有 l n α ~ l n β → − ∞ 又∵ 若 \alpha~\beta \to0^+,则有 ln\alpha ~ln\beta \to-\infty 又∵若α~β→0+,则有lnα~lnβ→−∞
∴ 由 等 价 无 穷 大 l n ( e x − 1 − x ) ~ l n 1 2 x 2 替 换 得 , 原 式 = e lim x → 0 + l n x 2 2 l n x ∴由等价无穷大ln(e^x-1-x)~ln{\frac{1}{2}x^2}替换得,原式=e^{\lim_{x\to0^+}{\frac{ln{\frac{x^2}{2}}}{lnx}}} ∴由等价无穷大ln(ex−1−x)~ln21x2替换得,原式=elimx→0+lnxln2x2
∴ 原 式 = e lim x → 0 + 2 l n x − l n 2 l n x = e 2 ∴原式=e^{\lim_{x\to0^+}{\frac{2lnx-ln2}{lnx}}}=e^2 ∴原式=elimx→0+lnx2lnx−ln2=e2
还可以尝试此题
题 目 : lim x → 0 + l n ( a r c t a n x ) l n [ l n ( 1 + x ) ] 题目:\lim_{x\to0^+}{\frac{ln(arctanx)}{ln[ln(1+x)]}} 题目:x→0+limln[ln(1+x)]ln(arctanx)
解的过程如下,这题利用等价无穷大可直接秒杀
∵ 若 α ~ β → 0 + , 则 有 l n α ~ l n β → − ∞ ∵ 若 \alpha~\beta \to0^+,则有 ln\alpha ~ln\beta \to-\infty ∵若α~β→0+,则有lnα~lnβ→−∞
∴ 原 式 = lim x → 0 + l n x l n x = 1 ∴ 原式=\lim_{x\to0^+}{\frac{lnx}{lnx}}=1 ∴原式=x→0+limlnxlnx=1
真题尝试
题 目 : lim x → + ∞ ( x 1 x − 1 ) 1 l n x 题目:\lim_{x\to + \infty}(x^{\frac{1}{x}}-1)^{\frac{1}{lnx}} 题目:x→+∞lim(xx1−1)lnx1

3.7当等价无穷小精度不够,使用泰勒展开
对 于 无 穷 小 而 言 , l i m 高 阶 低 阶 = 0 对于无穷小而言,lim\frac{高阶}{低阶}=0 对于无穷小而言,lim低阶高阶=0
故只需将分子展开到“余项均为分母的高阶无穷小”即可
两个函数相乘的泰勒展开,其中一个函数需要展开的最高阶数,取决于另一个函数展开后的最低阶数,二者相互影响,这其实是小学的乘法分配律的原理。
题 目 : lim x → 0 l n ( 1 + x ) l n ( 1 − x ) − l n ( 1 − x 2 ) x 4 题目:\lim_{x\to0}{\frac{ln(1+x)ln(1-x)-ln(1-x^2)}{x^4}} 题目:x→0limx4ln(1+x)ln(1−x)−ln(1−x2)
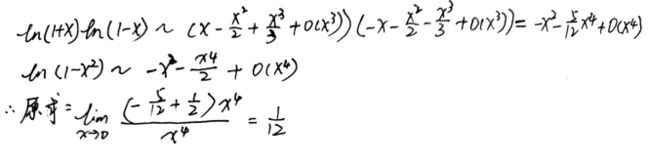
泰勒中值定理的应用
题 目 : 设 f ( x ) 在 x 0 处 二 阶 可 导 , 求 lim h → 0 f ( x 0 + 2 h ) − 2 f ( x 0 + h ) + f ( x 0 ) h 2 题目:设f(x)在x_0处二阶可导,求\lim_{h\to0}\frac{f(x_0+2h)-2f(x_0+h)+f(x_0)}{h^2} 题目:设f(x)在x0处二阶可导,求h→0limh2f(x0+2h)−2f(x0+h)+f(x0)
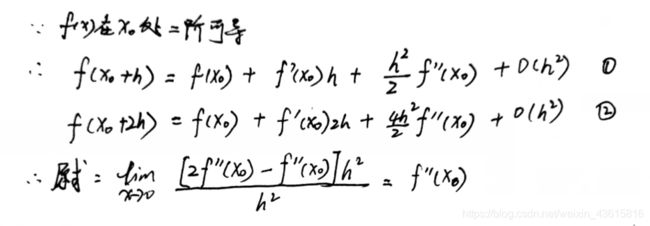
f ( x ) 在 x 0 处 n 阶 可 导 , f ( x ) 的 n 阶 导 数 在 x 0 领 域 内 不 一 定 可 导 f(x)在x_0处n阶可导,f(x)的n阶导数在x_0领域内不一定可导 f(x)在x0处n阶可导,f(x)的n阶导数在x0领域内不一定可导
但 是 f ( x ) 的 n − 1 阶 导 数 在 x 0 的 邻 域 内 一 定 存 在 , 由 导 数 定 义 得 来 但是f(x)的n-1阶导数在x_0的邻域内一定存在,由导数定义得来 但是f(x)的n−1阶导数在x0的邻域内一定存在,由导数定义得来
3.8无分母的泰勒展开
展开导最低次的系数合并后不为0时为止,说白了,就是展开导不能再抵消为止,此时,暴露出来的第一项,就是整个函数的等价无穷小。
题 目 : 请 寻 找 x → 0 时 , e x + c o s x − 2 − x 的 等 价 无 穷 小 题目:请寻找x\to0时,e^x+cosx-2-x的等价无穷小 题目:请寻找x→0时,ex+cosx−2−x的等价无穷小
解 题 过 程 : e x = 1 + x + x 2 2 + x 3 6 + o ( x 3 ) 解题过程:e^x = 1+x+\frac{x^2}{2}+\frac{x^3}{6}+o(x^3) 解题过程:ex=1+x+2x2+6x3+o(x3)
c o s x = 1 − x 2 2 + x 4 24 + o ( x 4 ) cosx = 1-\frac{x^2}{2}+\frac{x^4}{24}+o(x^4) cosx=1−2x2+24x4+o(x4)
e x + c o s x − 2 − x = x 3 6 + o ( x 3 ) e^x+cosx-2-x = \frac{x^3}{6}+o(x^3) ex+cosx−2−x=6x3+o(x3)
∴ e x + c o s x − 2 − x ~ x 3 6 ∴ e^x+cosx-2-x ~ \frac{x^3}{6} ∴ex+cosx−2−x~6x3