Pytorch实现RNN, GRU, LSTM模型
文章目录
-
- RNN
-
- 参数
- 代码
- GRU
-
- 公式
- 代码
- LSTM
-
- 公式
- 代码
如题,几个经典的NLP模型,Pytorch实现也比较简单,复杂的模型可以通过他们堆叠而成,比如encoder decoder这些。
RNN
首先是最简单的RNN,

他的模型最简单,就是当前时刻的input, 和上一时刻的hidden state,分别和一个W参数相乘,然后经过一个tanh门即可。还可以加上偏置项 b h b_h bh,在pytroch官方文档中,偏置项写了两个,但实际上用一个表示即可。
参数
可以设置的参数:
input_size : 输入x中的feature 数量
hidden_size: hidden state h的feature数量
num_layers: 模型层数,比如设置为2,就是StackedRNN, 第二个RNN会把第一个RNN的output拿来进行最终的计算。
nonlinearity: 设置激活函数为‘tanh’还是‘relu’,默认tanh
bias: 是否包含偏置项,默认True
batch_first: 如果True,input和output tensor的维度会是(batch, seq, feature),默认False
dropout: 设置dropout率,默认0,如果非0,会在除了最后一层的所有RNN output层加上dropout
bidirectional: 是否双向模型,默认False
模型输入,只有两个
input,维度为(seq_len, batch, input_size)
h_0, 维度为(num_layers * num_directions, batch, hidden_size)。
模型输出,只有两个
output: 包含最后一层RNN输出的,每一个t时刻的hidden state,维度是(seq_len, batch, num_directions * hidden_size)
h_n: t=seq_len 的hidden state,即最后时刻的hidden state,维度是(num_layers * num_directions, batch, hidden_size)
一般在模型里面初始化的时候会这样写
代码
self.rnn = nn.RNN(input_size, hidden_size, layers, bidirectional=True, batch_first=True)
默认前两个参数是输入和hidden的size
详细模型代码:
import torch.nn as nn
import torch.nn.functional as F
class RNN_Model(nn.Module):
def __init__(self):
super(RNN_Model, self).__init__()
self.rnn = nn.RNN(n_input, n_hidden, num_layers=1, batch_first =True)
self.linear = nn.Linear(n_hidden,n_class)
def forward(self, x):
rnn_output, h_n = self.rnn(x)
output = self.linear(rnn_output[:,-1,:])
# output = self.linear(h_n[-1])
return output
*特别注意一下这里rnn_output[:,-1,:] = h_n[-1], 无论num_layers是多少层,当bidirectional=False的时候rnn_output的最后一个永远等于h_n的最后一个,自行可以在代码中判断一下两个变量是否相等。
如果bidirectional=True,模型变成双向的,h_n的个数也会相应的翻倍(h_n的个数等于n_layers * n_direction),于是下一层的Linear的input_size也要乘2
模型如下
import torch.nn as nn
import torch.nn.functional as F
class Bi_RNN_Model(nn.Module):
def __init__(self):
super(Bi_RNN_Model, self).__init__()
self.rnn = nn.RNN(n_input, n_hidden, batch_first =True, bidirectional=True)
self.linear = nn.Linear(2*n_hidden,n_class)
def forward(self, x):
rnn_output, h_n = self.rnn(x)
# concat the last hidden state from two direction
hidden_out = torch.cat((h_n[-2,:,:],h_n[-1,:,:]),1)
output = self.linear(hidden_out)
return output
如果你验证一下你会发现rnn_output[:,-1,:]和torch.cat((h_n[-2,:,:],h_n[-1,:,:]),1)只有前一半相等,后一半不相等。。但你用这两种都是可以训练的,个人猜测原因是双向模型的反向hidden state是倒着存的。。
然后RNN存在的问题:梯度消失
显而易见,由于每一个时刻的output都由前一个时刻组成,那早期的输入就会嵌套很多层,从而使得学习得特别慢。
类似的,RNN也可以改成GRU, 他们的代码使用方式相似,GRU的好处是梯度消失的问题有一定缓解。
GRU

左边的reset gate和中间的upgate gate都是用sigmoid将当前时刻的 x t x_t xt和上一个时刻的hidden h t − 1 h_{t-1} ht−1进行计算
公式
reset gate:
r t = σ ( W r [ h t − 1 , x t ] + b r ) r_t = \sigma(W_r[h_{t-1}, x_t]+b_r) rt=σ(Wr[ht−1,xt]+br)
upgate gate:
z t = σ ( W z [ h t − 1 , x t ] + b z ) z_t = \sigma(W_z[h_{t-1}, x_t]+b_z) zt=σ(Wz[ht−1,xt]+bz)
如果reset gate趋近于0,则会忽略之前的memory,只保留词的信息
最左边的reset gate会和 h t − 1 h_{t-1} ht−1进行相乘,但不是直接相乘, h t − 1 h_{t-1} ht−1会经过一个参数处理
r t ∗ ( W h h t − 1 + b h ) r_t*(W_hh_{t-1}+b_h) rt∗(Whht−1+bh)
这个生成的结果会和当前时刻 x t x_t xt又一次合并,并且进入右边的蓝色tanh门
所以tanh门的输出为:
n t = t a n h ( W n x t + b n + r t ∗ ( W h h t − 1 + b h ) ) n_t = tanh(W_nx_t+b_n+r_t*(W_hh_{t-1}+b_h)) nt=tanh(Wnxt+bn+rt∗(Whht−1+bh))
从而可以获得最终的hidden state,他由刚才求的的tanh生成的结果 n t n_t nt和update gate的输出 z t z_t zt 一顿操作组合:
h t = ( 1 − z t ) ∗ n t + z t ∗ h t − 1 h_t = (1-z_t)*n_t+z_t*h_{t-1} ht=(1−zt)∗nt+zt∗ht−1
然后值得注意的是,如果你仔细看的话,图片里, ( 1 − z t ) (1-z_t) (1−zt)这个系数其实是乘在 h t − 1 h_{t-1} ht−1上的,但是从数学角度而言,这里没有区别,反正 n t n_t nt和 h t − 1 h_{t-1} ht−1的系数加起来为1就行,
于是就成了 h t = A ∗ n t + B ∗ h t − 1 , w h e r e A + B = 1 h_t = A*n_t+B*h_{t-1}, where\ A+B=1 ht=A∗nt+B∗ht−1,where A+B=1,个人感受是这个思想就是门控(Gated)。。所以他才叫GRU(Gated Recurrent Unit 门控循环单元)。
公式总结:
r t = σ ( W r [ h t − 1 , x t ] + b r ) z t = σ ( W z [ h t − 1 , x t ] + b z ) n t = t a n h ( W n x t + b n + r t ∗ ( W h h t − 1 + b h ) ) h t = ( 1 − z t ) ∗ n t + z t ∗ h t − 1 r_t = \sigma(W_r[h_{t-1}, x_t]+b_r)\\ z_t = \sigma(W_z[h_{t-1}, x_t]+b_z)\\ n_t = tanh(W_nx_t+b_n+r_t*(W_hh_{t-1}+b_h))\\ h_t = (1-z_t)*n_t+z_t*h_{t-1} rt=σ(Wr[ht−1,xt]+br)zt=σ(Wz[ht−1,xt]+bz)nt=tanh(Wnxt+bn+rt∗(Whht−1+bh))ht=(1−zt)∗nt+zt∗ht−1
代码
class GRU_Model(nn.Module):
def __init__(self):
super(GRU_Model, self).__init__()
self.gru = nn.GRU(n_input, n_hidden, num_layers=1, batch_first =True)
self.linear = nn.Linear(n_hidden,n_class)
def forward(self, x):
gru_output, h_n = self.gru(x)
output = self.linear(gru_output[:,-1,:])
# output = self.linear(h_n[-1])
return output
双向的:
class Bi_GRU_Model(nn.Module):
def __init__(self):
super(Bi_GRU_Model, self).__init__()
self.gru = nn.GRU(n_input, n_hidden, batch_first =True, bidirectional=True)
self.linear = nn.Linear(2*n_hidden,n_class)
def forward(self, x):
gru_output, h_n = self.gru(x)
# concat the last hidden state from two direction
hidden_out = torch.cat((h_n[-2,:,:],h_n[-1,:,:]),1)
output = self.linear(hidden_out)
#output = self.linear(gru_output[:, -1, :])
return output
LSTM
接下来就是LSTM
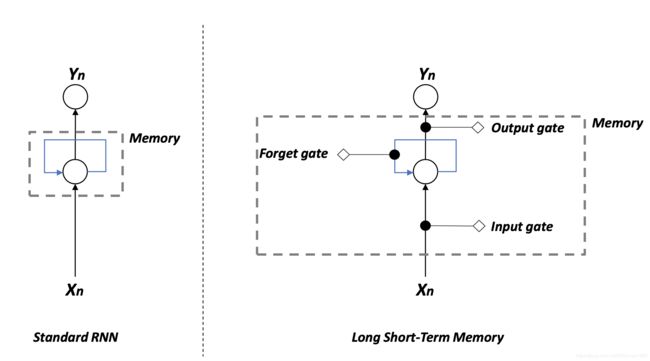
LSTM的参数量是RNN的大约4倍。
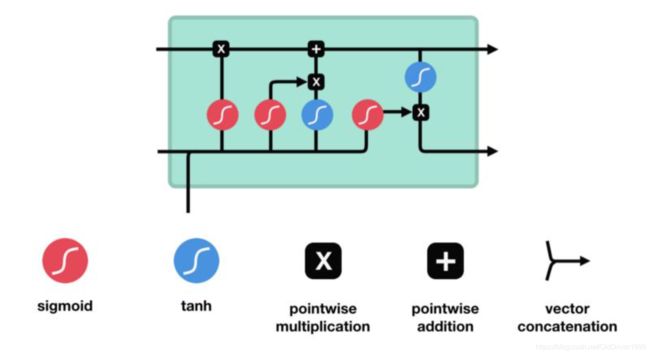
通过门来减轻梯度消失
公式
其中红色门是sigmoid,比如左边第二个红色sigmoid就是对当前时刻的输入 x t x_t xt和上个时刻的hidden state h t − 1 h_{t-1} ht−1进行操作, 产生一个 i t i_t it,其中 b i b_i bi
是偏置项
i t = σ ( W i [ h t − 1 , x t ] + b i ) i_t = \sigma(W_i[h_{t-1}, x_t]+b_i) it=σ(Wi[ht−1,xt]+bi)
sigmoid结果在[0,1]之间,越接近于0表示遗忘,越接近1表示保留。
类似的,中间那个蓝色的门会 x t x_t xt和 h t − 1 h_{t-1} ht−1进行tanh操作, 产生一个 C ~ t \tilde{C}_t C~t:
C ~ t = t a n h ( W C [ h t − 1 , x t ] + b C ) \tilde{C}_t = tanh(W_C[h_{t-1},x_t]+b_C) C~t=tanh(WC[ht−1,xt]+bC)
其中C是memory cell。
然后会把sigmoid的结果和tanh的结果相乘。
sigmoid的结果是在区间[0,1]的,他和tanh的结果相乘之后会决定那些人保留,哪些遗忘。
类似的左边第一个sigmoid也是个遗忘门,会产生一个 f t f_t ft。
f t = σ ( W f [ h t − 1 , x t ] + b f ) f_t=\sigma(W_f[h_{t-1},x_t]+b_f) ft=σ(Wf[ht−1,xt]+bf)
于是只看最上面一条线,关于memory cell的生成
C t = f t ∗ C t − 1 + i t ∗ C t ~ C_t = f_t*C_{t-1}+i_t*\tilde{C_t} Ct=ft∗Ct−1+it∗Ct~
最后一步,确定右下角,当前时刻hidden state
这里会用到刚才新生成的C,以及另一个遗忘门的结果:
遗忘门结果:
o t = σ ( W o [ h t − 1 , x t ] + b o ) o_t=\sigma(W_o[h_{t-1}, x_t]+b_o) ot=σ(Wo[ht−1,xt]+bo)
tanh门结果:
h t = o t ∗ t a n h ( C t ) h_t = o_t*tanh(C_t) ht=ot∗tanh(Ct)
相乘的原因是用来决定哪些信息需要被保留。
总结起来就是这6个公式,pytorch doc中稍有不同,但大致一样
i t = σ ( W i [ h t − 1 , x t ] + b i ) C ~ t = t a n h ( W C [ h t − 1 , x t ] + b C ) f t = σ ( W f [ h t − 1 , x t ] + b f ) C t = f t ∗ C t − 1 + i t ∗ C t ~ o t = σ ( W o [ h t − 1 , x t ] + b o ) h t = o t ∗ t a n h ( C t ) i_t = \sigma(W_i[h_{t-1}, x_t]+b_i)\\ \tilde{C}_t = tanh(W_C[h_{t-1},x_t]+b_C)\\ f_t=\sigma(W_f[h_{t-1},x_t]+b_f)\\ C_t = f_t*C_{t-1}+i_t*\tilde{C_t}\\ o_t=\sigma(W_o[h_{t-1}, x_t]+b_o)\\ h_t = o_t*tanh(C_t) it=σ(Wi[ht−1,xt]+bi)C~t=tanh(WC[ht−1,xt]+bC)ft=σ(Wf[ht−1,xt]+bf)Ct=ft∗Ct−1+it∗Ct~ot=σ(Wo[ht−1,xt]+bo)ht=ot∗tanh(Ct)
注意,每一个sigmoid中的参数W是不一样的。
从模型可知,LSTM会多产生一个memory cell的输出,所以代码中他就有3个output。
代码
class LSTM_Model(nn.Module):
def __init__(self):
super(LSTM_Model, self).__init__()
self.lstm = nn.LSTM(n_input, n_hidden, num_layers=1, batch_first =True)
self.linear = nn.Linear(n_hidden,n_class)
def forward(self, x):
lstm_output, (h_n, c_n) = self.lstm(x)
output = self.linear(lstm_output[:,-1,:])
# output = self.linear(h_n[-1])
return output
这里用h_n[-1]也是可以的,跟前面类似
双向的:
class Bi_LSTM_Model(nn.Module):
def __init__(self):
super(Bi_LSTM_Model, self).__init__()
self.lstm = nn.LSTM(n_input, n_hidden, num_layers=1, batch_first =True)
self.linear = nn.Linear(2*n_hidden,n_class)
def forward(self, x):
lstm_output, (h_n, c_n) = self.lstm(x)
output = self.linear(lstm_output[:,-1,:])
# output = self.linear(torch.cat((h_n[-2], h_n[-1]), 1))
return output
