幂律分布专题
幂律分布
幂律分布的数学形式
广义形式:
幂律分布的广义形式即是反映了一个幂次反比关系 p ( x ) ∝ x − α p(x) \propto x^{-\alpha} p(x)∝x−α ,其中 α \alpha α 的通常取值为 2 < α < 3 2<\alpha<3 2<α<3。
精确形式:
在对原有幂律分布函数加以分析可以看出,当 x → 0 x \rightarrow 0 x→0 时,幂律分布的概率密度函数发散。随机变量不会在整个 x ≥ 0 x \geq 0 x≥0取值范围内服从幂律分布,更可能在大于某个幂律下界 x min x_{\min } xmin之后,随机变量 X X X的尾巴部分服从幂律分布。因而,现有的针对幂律分布分析多基于以下数学形式
连续情形:
概率密度函数: p ( x ) d x = Pr ( x ≤ X < x + d x ) = C x − α d x p(x) \mathrm{d} x=\operatorname{Pr}(x \leq X
根据概率规范性(归一化参数): ∫ x min ∞ C f ( x ) d x = 1 \int_{x_{\min }}^{\infty} C f(x) \mathrm{d} x=1 ∫xmin∞Cf(x)dx=1
离散情形:
概率质量函数: p ( x ) = Pr ( X = x ) = C x − α p(x)=\operatorname{Pr}(X=x)=C x^{-\alpha} p(x)=Pr(X=x)=Cx−α
假设x的取值为离散整数
进行归一化参数计算 ∑ x = x min ∞ C f ( x ) = 1 \sum_{x=x_{\min }}^{\infty} C f(x)=1 ∑x=xmin∞Cf(x)=1可以得到:
p ( x ) = x − α ζ ( α , x min ) p(x)=\frac{x^{-\alpha}}{\zeta\left(\alpha, x_{\min }\right)} p(x)=ζ(α,xmin)x−α
其中,
ζ ( α , x min ) = ∑ n = 0 ∞ ( n + x min ) − α \zeta\left(\alpha, x_{\min }\right)=\sum_{n=0}^{\infty}\left(n+x_{\min }\right)^{-\alpha} ζ(α,xmin)=n=0∑∞(n+xmin)−α
常见分布在截断形式下的归一化参数:
其中,指数分布和对数正态分布在图像上和幂律分布图像相似程度较高,在数据拟合和假设验证的过程中容易混淆,需要加以区分
幂律分布的形成机制
根本原因:节点增长 & 优先连接
针对复杂网络中普片存在的幂律分布现象,其呈现幂律的两个最根本原因在于:(Barabasi & Albert )
- 成长性(growth):是指网络节点数的增加
- 优先连接性(preferential attachment):是指新加入的节点总是优先选择与度值较高的节点相连
注:“优先连接”并适用于所有出现幂律分布的情况,即是对于某些无标度网络,使用优先连接特性解释幂律分布也不甚合理。
动力学原因:自组织临界 理论
自组织临界理论一直被视为产生幂律分布的动力学成因,幂律也可以作为自组织临界的证据。对于自组织临界的理解可以联系沙堆模型和雪崩效应。
幂律分布是自组织临界系统在混沌边缘,即从稳态过渡到混沌态的一个标志,可以预测系统的相位和相变。幂律分布认为,由大量相互作用的成分组成的系 统会自然地向自组织临界态发展;当系统达到这种 状态时,即使是很小的干扰事件也可能引起系统发 生一系列灾变。
-
自组织的含义:自组织的含义是指该状态的形成主要由系统内部各组成成分之间的相互作用产生,而不是由任何外界因素控制或主导所致。
自组织过程实质上是一个减熵有序化的过程。例如,在沙堆模型中,沙粒的堆积过程就是一个自组织过程。在自组织过程中,局部可能出现沙崩,但是随着沙粒规模的增大,沙堆的坡度仍然维持在临界值以内,不会出现沙堆坍塌的效果。
-
临界态:临界态是指系统处于一种特殊的敏感状态,微笑的局部变化可以不断的被放大,进而扩散至整个系统。
- 对于自组织临界理论,其关键信息在于以下三点:
- 自组织过程:系统的增长呈现一定规律
- 临界过程:由稳态过渡到混沌态的一个标志,规模可以看作是自组织过程的最大值,当其超过规定阈值时,将会出现系统的“大沙崩”。
- 微小扰动:自组织临界状态只是漫长变化过程中的一个临界点,是由量变达到质变的分界。自组织临界状态是脆弱的,一旦施加以微小扰动,系统状态便会发生突变。
HOT理论
在世纪之交,物理学家卡尔森(J. M. Carlson)和控制学者道尔(John Doyle)在物理学期刊上提出了设计系统中的幂律产生机制——高度优化容忍(Highly Optimized Tolerance),用以表征一些复杂互连系统可以有效地容忍某些不确定因素(即鲁棒性),也会对其它未被考虑到的不确定因素变得更敏感(即脆弱性)。
当一复杂系统处于HOT状态时,该系统将满足幂律,也就是说,全局性的优化过程可导致幂律分布:具有特征尺度的输入经过一个全局性的系统“产量”优化过程后,可产生具有幂律分布特性的输出。
随机过程
某些随机过程可以产生幂律分布。例如随机游走模型可以解释物种寿命所呈现出的幂律分布。
“随机行走模型”可以解释物种寿命所呈现的幂律分布。另外,“Yule过程”是一个生成幂律比较通用的机制,通过调节参数,可以产生幂指数范围宽广的幂律分布,并可与世纪观测值相一致。
幂律分布的参数估计
非线性回归
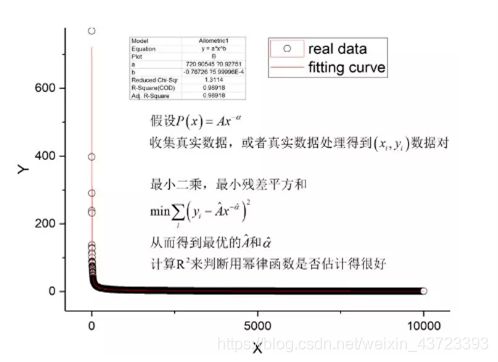
通过直方图直接进行非线性回归,并且直接得到参数的估计置信区间和说明拟合效果的决定系数。如果决定系数越大说明幂律分布函数拟合效果越好。这里面的最小二乘法的思想是使得残差平方和最小。
对数线性回归
幂律分布形式:
P ( x ) = c x − α P(x)=c x^{-\alpha} P(x)=cx−α
原理:线性关系
ln P ( x ) = ln c − α ln x \ln P(x)=\ln \mathrm{c}-\alpha \ln x lnP(x)=lnc−αlnx
可以通过观察 l n P ( x ) lnP(x) lnP(x)和 l n x lnx lnx 是否满足线性关系简单判断随机变量是否服从幂律分布。在双对数坐标系下,概率密度近似成一条直线,可以通过最小二乘拟合的方法计算直线斜率,我们所需要的尺度参数就是直线斜率的相反数。
局限性:
1.对数直线不唯一
在双对数坐标系下,指数分布和对数正态分布图像也近似成一条直线,这种几何特性并非幂律分布所独有的。
2.尾部噪声
根据幂律分布的长尾特性,随机变量在尾部取值较多而且分散,在尾部数据发生波动时容易影响参数估计的效果,尾部噪声会使得结果产生非常大的偏移。
因此,在双对数图上进行对数线性回归不能准确判定数据是否遵循幂律分布,也就是说,直线特性是幂律分布的必要不充分条件。对数线性回归在参数估计上存在显著误差。双参数直线估计适用于幂律分布的初步判断以及进行粗略地参数估计。
Exponential Binning
Python通过Exponential binning和线性回归对幂律分布的参数 α \alpha α进行估计时,考虑到尾部噪声的问题,提出了减少箱子的数量以减少尾部的噪声点,但是由于幂律分布的数据大多集中在前段,减少箱子的数量会导致数据细节的迅速丢失。
采用logarithmic bins进行装箱,可以达到既要减小尾部数据占有的箱子数,又要保证头部数据的箱子个数足够多来保留更多细节的目的这样的分割方法是前密后疏,
极大似然估计(MLE)
- 概率连乘
- 对数求导 —— 似然函数
连续情形:
α ^ = 1 + n [ ∑ i = 1 n ln X i x min ] − 1 \hat{\alpha}=1+n\left[\sum_{i=1}^{n} \ln \frac{X_{i}}{x_{\min }}\right]^{-1} α^=1+n[i=1∑nlnxminXi]−1
标准误差:
σ = α ^ − 1 n + O ( 1 / n ) \sigma=\frac{\hat{\alpha}-1}{\sqrt{n}}+\mathrm{O}(1 / n) σ=nα^−1+O(1/n)
离散情形:
α ^ ≃ 1 + n [ ∑ i = 1 n ln x i x min − 1 2 ] − 1 \hat{\alpha} \simeq 1+n\left[\sum_{i=1}^{n} \ln \frac{x_{i}}{x_{\min }-\frac{1}{2}}\right]^{-1} α^≃1+n[i=1∑nlnxmin−21xi]−1
标准误差:
σ = 1 n [ ζ ′ ′ ( α ^ , x min ) ζ ( α ^ , x min ) − ( ζ ′ ( α ^ , x min ) ζ ( α ^ , x min ) ) 2 ] \sigma=\frac{1}{\sqrt{n\left[\frac{\zeta^{\prime \prime}\left(\hat{\alpha}, x_{\min }\right)}{\zeta\left(\hat{\alpha}, x_{\min }\right)}-\left(\frac{\zeta^{\prime}\left(\hat{\alpha}, x_{\min }\right)}{\zeta\left(\hat{\alpha}, x_{\min }\right)}\right)^{2}\right]}} σ=n[ζ(α^,xmin)ζ′′(α^,xmin)−(ζ(α^,xmin)ζ′(α^,xmin))2]1
通过计算参数的期望和方差可以得到:对于连续性幂律分布,不存在参数的有效无偏估计,而存在渐进无偏估计。
Kolmogorov–Smirnov估计
幂律分布指数参数的Kolmogorov–Smirnov估计和检验也是万能的“魔戒”。
具体做法:
使用极大似然方法估计幂律模型参数;
计算数据和幂律之间的拟合优度,以判定幂律是否为合理假设;
通过似然比检验比较幂律假设和其他分布假设,以判断更倾向于哪个假设。
幂律分布的图形化验证方法
log-log图
在双对数图上呈现直线是必要的,但是没有足够的证据证明它们的幂律关系,直线斜率就对应于幂律指数。因此,双对数图只适用于初步判断幂律分布和排除其他概率分布。
Pareto Q-Q图
这种方法利用残余分位函数束验证分布尾部是否遵循幂律。
帕累托Q-Q图的绘制步骤:它将取对数后样本数据的分位数与取均值为1的指数分布对应的分位数(或标准帕累托分布的位数)进行比较。如果得到的散点图表现是“渐近收敛”为直线,就应该推测其可能服从幂律分布。帕累托 Q-Q图的局限是它在尾部指数α接近于0时表现不佳,因为帕累托Q-Q图难以检验尾部是缓慢变化的分布。
平均剩余寿命图
检验幂律概率分布的方法是平均剩余寿命图,它包含以下步骤:首先对数据取对数,然后将高于第 i 阶统计量的数据平均值与第$ i 阶 统 计 量 进 行 比 较 绘 制 , 从 阶统计量进行比较绘制,从 阶统计量进行比较绘制,从i = 1,2,…, n$,其中n是随机样本容量。如果绘制出的散点图走势呈现为一条“稳定”的水平直线,那么应该考虑其服从幂律分布。但由于平均剩余寿命图对异常值非常敏感(它并不稳健),所以它通常会产生一些难以解释的图形
幂律分布的研究历史
幂律分布的研究历史涉及到诸多学科,总体上可以分为三个部分:定性研究、定量研究和动力机制研究。其研究历史总体上经历了“有现象到本质,由宏观到微观,由定性到定量,由时间到空间,由结构到过程”的不断深化过程。[8]
幂律分布的定性研究
在19世纪末至21世纪初,众多领域的学者独立地进行研究,但都心有灵犀,不约而同地发现了幂律分布这一规律。具体地,关于幂律特性定性研究发展的时间脉络如下。
追根溯源:帕累托分布 ( Pareto Distribution ),1897
“幂律概念”最早可以追溯到1897年意大利经济学家维尔弗雷多·帕累托 ( Vilfredo Pareto )发现财富分配的“可预料的不均衡”现象,即现今熟知的“二八原则”。
-
韦伯和法约尔“官僚组织模式”中的科层制 ( Bureaucracy System ),1911-1916
-
拉扎斯菲尔德多级传播理论中的意见领袖 ( Opinion Leader ),1948
-
西蒙在经济学研究中的 “西蒙模型” ( Simon Model ),1955
-
哈耶克的涌现理论 ( Emergence Theory ),1964
-
汪丁丁在行为经济学中提出的黏着偏好原理 ( Preferential Attachment),2010
-
姜奇平认为幂律分布是互联网技术结构和经济结构中的关键特征,2012
幂律分布的定量研究
现今,关于幂律分布定量研究的理论灿若繁星,例如小世界现象、无标度网络模型、长尾模型、曲棍球杆型增长和 K 核心分布等,这些都是对幂律分布不同侧面的挖掘过程。幂律分布的定量研究历史时间轴如下。
追根溯源:齐普夫定律 ( Zipf’s Law ),1949
齐普夫发现了语言词频幂律分布规律,即在自然语言的语料库里,一个单词出现的频率与它在频率表里的排名成反比。
-
艾尔多斯和莱利在数学图论中发现了复杂网络的拓扑结构 ( Complex Network Topological Structure ),1959
-
曼德布罗特在研究棉花价格浮动时所发现的肥尾现象 ( Fat Tail ),1963
-
史蒂夫·斯托加茨和邓肯·瓦茨在网络数学中发现的“小世界现象” ( Small-world Phenomenon ) ,1998
-
巴拉巴西和艾尔伯特的无标度网络模型 ( Scale Free Network ),1999
-
胡伯曼的网络“幂律增长”法则 ( Power Law ),2002
-
安德森的长尾模型 ( The Long Tail Module ),2004
-
IBM、Compaq 和 AltaVista 的 “领结理论 ” ( Bow-tie Theory ) ,2006
-
社会化媒体分析公司SysomosInc发现Twitter的“曲棍球杆型增长”( Hockeystick-type Growth ),2009
-
加西亚的 “K 核心分布” ( K-core Distribution ),2013
-
马西克—弗罗杰的 “人类神经元连接如同社交网络” ( Human Nerve System likes Social Network ),2015
幂律分布的动力机制研究
19世纪末至整个20世纪,一些心理学和网络研究开始探索社会群体动力机制,虽然并不是全部围绕幂律分布展开的,却能部分解释其动力来源,比如塔尔德的模仿律和阿希的从众理论; 一些多学科研究则开始寻觅大型社会网络的形成动因,比如繆尔达尔的循环积累因果联系学说和梅特卡夫网络价值定律等。
关于幂律分布的动力学成因,整体上看,现在仍然处在萌芽时期,现如今的研究不全面、不系统、不深入,零星发散,探幽发微,需要更加成熟的理论进行完善,期待更多的学者进行归纳整合,深入挖掘幂律长尾背后的动因。