算法合集：前缀和——听说有人说我简单？

前缀和是dp的一种表现形式，更像是技巧性的算法，虽难度比不上dp，也比较容易想到，但前缀和的分类统计等衍生思想还是可以借鉴的
题目中对前缀和的暗示是比较明显的，一般提到连续子数组就可以往前缀和方向引了。
下面直接从前缀和的实战开始总结前缀和的思想
另外由于自己刷题过程中没有刻意统计，所以暂时呈现的题目数量不多

一、一维前缀和

1、前后缀和：还可以从后往前

1）题目一：LeetCode 238 除自身以外数组的乘积（要求时间O(n)，空间O(1)，且不能用除法）
拿下面的斐波拉契数列来举例子

给数组的两侧填1让分析更直观些

基于dp的分析： 对于数组中任意的一个数，如果知道其左右两侧的连乘结果，就可以得到当前的答案
动态分析： 倘若求2右侧连乘的结果，就得知道3右侧的结果，继而得要知道5右侧的结果。左侧同理，欲求21左侧连乘的结果，需要一直推出2左侧的结果

• 定义数组plus为前缀和数组
• :plus[i]表示nums[i]左侧连乘，plus[i]:表示nums[i]右侧连乘
• :plus[i] = :plus[i - 1] * nums[i - 1]
• plus[i]: = plus[i + 1]: * nums[i + 1]

所以先从左到右、再从右到左两次遍历即可

public int[] productExceptSelf(int[] nums) {
    int len = nums.length;
    int[] ans = new int[len];
    ans[0] = 1;
    for (int i = 1; i < len; i++)
        ans[i] = ans[i - 1] * nums[i - 1];
    int plus = nums[len - 1];
    for (int i = len - 2; i >= 0; i--) {
        ans[i] *= plus;
        plus *= nums[i];
    }
    return ans;
}

2）题目二：LeetCode 926 将字符串翻转到单调递增
对这题的把控其实就在：我们应从哪里开始将0置1？

• 极端情况一：从i = 0的位置开始置1，使得s全为1
• 极端情况二：完全不不置1，使得s全为0

然后便是前缀和的精妙所在了

• 对于从任意一个位置i，假设从此处开始置1
• 也就是将[0, i)中所有的1置0，我们用数组count1记录[0, i)中1的数目
• 同时，将[i, s.length - 1]中所有0置1，我们用数组count0记录[i, s.length - 1]中0的数目

int[] count1 = new int[len + 1]; // 从左往右数，不包括当前
int[] count0 = new int[len + 1]; // 从右往左数，包括当前

为什么要长度+1？ 因为考虑极端情况二，如果完全不置1，我们需要在字符串s的末尾假想一个位置，来统计s中0的数量

public int minFlipsMonoIncr(String s) {
    int len = s.length();
    int ans = (int)1e9;
    int[] count1 = new int[len + 1]; // 从左往右数，不包括当前
    int[] count0 = new int[len + 1]; // 从右往左数，包括当前
    for (int i = 1; i <= len; i++)
        count1[i] = count1[i - 1] + (s.charAt(i - 1) == '1' ? 1 : 0);
    for (int i = len - 1; i >= 0; i--)
        count0[i] = count0[i + 1] + (s.charAt(i) == '0' ? 1 : 0);
    for (int i = 0; i <= len; i++)
        ans = Math.min(ans, count1[i] + count0[i]);
    return ans;
}

2、结合HashMap求target：两数之和思想

HashMap是老生常谈的前缀和的搭配方式了
1）例题：LeetCode 1074 元素和为目标值的子矩阵数量
乍一看，思路比较清晰，暴力方法O(n4)——求二维前缀和，四个for循环找数量即可
但这题的思想是二维压成一维的dp思想，动图可以参考这篇题解：动图演示——前缀和降维
还是拿斐波拉契数列来举例子：

给定一个一维数组，其前缀和很好求，sum[i] = sum[i - 1] + nums[i]

倘若给定两个一维数组呢？

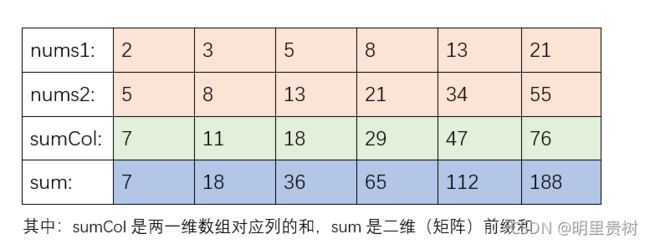
发现没有，对长度相同的数组，求和对应列（行）得到一维数组，对该数组求前缀和即为二维（矩阵）前缀和。此题便是通过压缩的方式来降低时间复杂度
然后此题衍化成：对一维数组求target。对具体代码便不做分析了

public int numSubmatrixSumTarget(int[][] matrix, int target) {
	int ans = 0;
	int rows = matrix.length, cols = matrix[0].length;
	for (int i = 0; i < cols; i++) { // 左边界
        int[] sum = new int[rows]; // 行前缀和
        for (int j = i; j < cols; j++) { // 右边界
            for (int k = 0; k < rows; k++)
                sum[k] += matrix[k][j];
            ans += calSumTarget(sum, target);
        }
    }
    return ans;
}

private int calSumTarget(int[] sum, int target) {
    HashMap<Integer, Integer> map = new HashMap<>(); // sum, 数量
    int res = 0;
    int s = 0; // 一维数组的前缀和
    map.put(0, 1);
    for (int x : sum) {
        s += x;
        res += map.getOrDefault(s - target, 0);
        map.put(s, map.getOrDefault(s, 0) + 1);
    }
    return res;
}

关于calSumTarget()函数，若不懂可以先解决下面的实战题目再回看
2）实战题目：经典的LeetCode 1 两数之和模板
LeetCode 560 和为K的子数组
LeetCode 930 和相同的二元子数组

3、分类统计

前缀和还可以方便分类来统计
1）例题一：LeetCode 523 连续的子数组和
这题最巧妙的思想是将统计前缀和转化为统计取余后的过量值

每次求前缀和后对k取余
套用两数之和的思想，若当前的取余结果已经出现过了，那么他们相差了k的倍数
相当于我们依据k给所有前缀和分类，去找到同一类的是否出现过

最后注意一下题目要求的数组长度即可

public boolean checkSubarraySum(int[] nums, int k) {
    if (nums.length == 1)
        return false;
    HashMap<Integer, Integer> map = new HashMap<>();
    map.put(0, -1);
    int sum = 0;
    for (int i = 0; i < nums.length; i++) {
        sum = (sum + nums[i]) % k;
        if (map.containsKey(sum)) {
            if (i - map.get(sum) > 1)
                return true;
        } else {
            map.put(sum, i);
        }
    }
    return false;
}

2）例题二：LeetCode 525 连续数组
此题的关键是有明显的分类信号：统计0和1的数量

由于0的存在，使得我们难以统计0和1各自的数量
为了抵消0和1之间的相互干扰，我们将0全部变成-1
套用两数之和的模板，由于影响相互抵消了，若当前的前缀和出现过，计算长度即可
题目就变成了target = 0的模式

public int findMaxLength(int[] nums) {
    HashMap<Integer, Integer> map = new HashMap<>();
    int sum = 0;
    int ans = 0;
    map.put(0, -1);
    for (int i = 0; i < nums.length; i++) {
        sum += nums[i] == 0 ? -1 : 1;
        if (!map.containsKey(sum))
            map.put(sum, i);
        else
            ans = Math.max(ans, i - map.get(sum));
    }
    return ans;
}

3）实战题目：
LeetCode 1248 统计[优美子数组]

4、万花筒的前缀和搭配

1）例题：LeetCode 528 按权重随机选择（前缀和 + 二分）
权重类型的题目很自然的想到求和并计算占比
类比下面的例子：

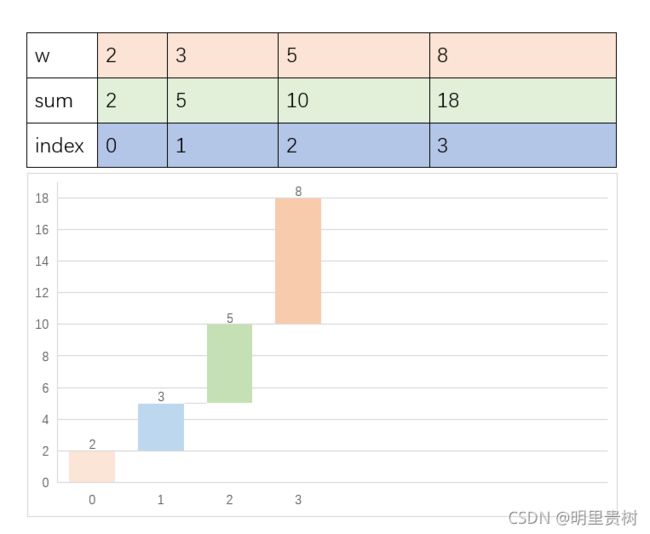
首先我们计算出了sum = 18
想象此时有18块蛋糕，我们给每块蛋糕编号1 ~ 18
其中1~2号蛋糕给第0个小朋友吃，3~5号蛋糕给第1个小朋友吃，以此类推
那么对于任意一个蛋糕x，我们是否可以计算出这个蛋糕是哪个小朋友的？

吐槽一下Excel的图表真是拉跨

随机生成一个1 ~ 18的数random，找到第一个 >= random的sum即可确定index

这里寻找第一个 >= target的数，属于lower_bound的模板，之前的博客中介绍过：算法合集：二分——pdd每次都能砍一半吗？这里不多赘述

int[] sum;
Random random;
public Solution(int[] w) {
    this.sum = new int[w.length];
    this.random = new Random();
    sum[0] = w[0];
    for (int i = 1; i < w.length; i++)
        sum[i] = sum[i - 1] + w[i];
}
    
public int pickIndex() {
    int val = random.nextInt(sum[sum.length - 1]) + 1;
    // 找到第一个 >= val的数
    int l = 0, r = sum.length - 1;
    while (l < r) {
        int mid = (l + r) >> 1;
        if (sum[mid] >= val)
            r = mid;
        else
            l = mid + 1;
    }
    return l;
}

2）实战题目：
LeetCode 209 长度最小的子数组（前缀和 + 二分）
LeetCode 327 区间和个数（前缀和 + 树状数组/线段树/归并）
对于题目327的树状数组的讲解可以参看之前写的树状数组专讲：数据结构：树状数组：姐来展示下什么叫高端前缀和

二、二维前缀和：dp缩影

听上去升维会变难了，但难度反而降了，通过下面的题目来展开：
例题：LeetCode 304 二维区域和检索-矩阵不可变

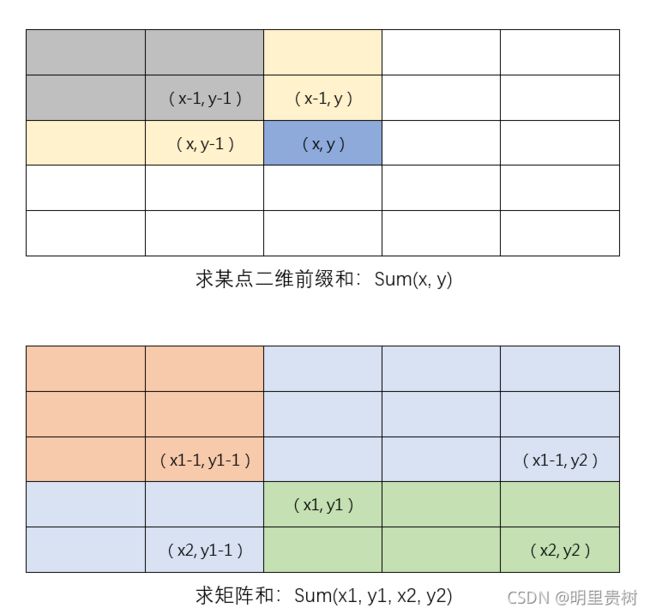
其实就是最基础的dp形式，便不展开讲解了，结合下面代码在脑中绘图食用更加
其实难点在边界处理
下面提供两种边界处理方法：
1、越界取0： 另外写一个函数控制是否出界，出界则返回0

int[][] s;
public NumMatrix(int[][] matrix) {
    int row = matrix.length;
    int col = matrix[0].length;
    s = new int[row][col];
    for (int i = 0; i < row; i++)
        for (int j = 0; j < col; j++)
            s[i][j] = matrix[i][j] + getSum(i - 1, j) + getSum(i, j - 1) 
            			- getSum(i - 1 , j - 1);
}

public int sumRegion(int row1, int col1, int row2, int col2) {
    return getSum(row2, col2) - getSum(row2, col1 - 1) - getSum(row1 - 1, col2)
    		 + getSum(row1 - 1, col1 - 1);
}

private int getSum(int i, int j) {
    if (i == -1 || j == -1)
        return 0;
    return s[i][j];
}

2、增大前缀和数组： 给前缀和数组长宽都+1，防止越界，不过要注意下标对应

int[][] s;
public NumMatrix(int[][] matrix) {
    int rows = matrix.length, cols = matrix[0].length;
    s = new int[rows + 1][cols + 1];
    for (int i = 1; i <= rows; i++)
        for (int j = 1; j <= cols; j++)
            s[i][j] = matrix[i - 1][j - 1] + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
}
    
public int sumRegion(int row1, int col1, int row2, int col2) {
    return s[row2 + 1][col2 + 1] - s[row2 + 1][col1] - s[row1][col2 + 1] + s[row1][col1];
}