LeetCode刷题-数组
LeetCode刷题-数组
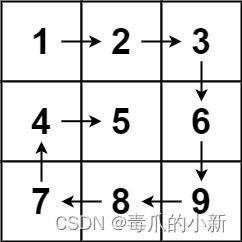
数组的遍历
485.最大连续1的个数
思路:当前nums[i]为1就计数加一,否则清零
public int findMaxConsecutiveOnes(int[] nums) {
int count = 0;
int result = 0;
for (int i=0;i<nums.length;i++){
if (nums[i]==1){
count++;
result = Math.max(result,count);
}else{
count = 0;
}
}
return result;
}
495.提莫攻击
如果timeSeries[i+1]在timeSeries[i]+duration之间
即下一个开始中毒的时间在上一个中毒的时间区间中
那么中毒时间为:timeSeries[i+1]-timeSeries[i]
否则中毒时间为:duration
public int findPoisonedDuration(int[] timeSeries, int duration) {
if (timeSeries.length==1){
return duration;
}else {
int result = 0;
for (int i = 0;i<timeSeries.length-1;i++){
if (timeSeries[i]+duration>=timeSeries[i+1]){
result += timeSeries[i+1]-timeSeries[i];
}else {
result += duration;
}
}
//最后一个时间点一定会中毒
return result+duration;
}
}
414.第三大的数
如果数组长度大于等于3,开始遍历
计数count,每次满足下一个数字和上一个数字不一样,count加一
有两次不一样即找到了第三大的元素
public int thirdMax(int[] nums) {
//得到升序的数组
int[] reverseArray = new Reverse().reverseArray(nums);
//如果数组的数量长度小于2,那么直接返回最大元素
if (reverseArray.length<=2){
return reverseArray[0];
}else {
int result = reverseArray[0];
int count = 0;
for (int i=1;i<reverseArray.length;i++){
if (reverseArray[i]!=reverseArray[i-1]){
result = reverseArray[i];
count++;
//特别要注意,如果count小于2就遍历完了整个数组
//表明重复元素很多,则直接返回数组中的最大数
if (count==2){
break;
}else {
result = reverseArray[0];
}
}
}
return result;
}
}
//降序排列数组
class Reverse{
public int[] reverseArray(int[] a){
//先升序排列,然后调换头尾对应的位置
Arrays.sort(a);
for (int i=0;i<a.length/2;i++){
int temp;
temp = a[i];
a[i] = a[a.length-i-1];
a[a.length-i-1] = temp;
}
return a;
}
}
因为数组没有自带的降序排列方法,我们需要自定义排序,除了上述排序,还有如下排序
public int[] reverseArray(int[] a){
//先升序排列,然后调换头尾对应的位置
Arrays.sort(a);
int start = 0,end = a.length-1;
while (start<end){
int temp;
temp = a[start];
a[start] = a[end];
a[end] = temp;
start++;
end--;
}
return a;
}
628.三个数的最大乘积
不能简单的直接排序之后最后三个数相乘
- 如果全为正数或者负数,直接返回最后三个数字相乘
- 如果有正数有负数
返回max(三个最大正数的乘积,两个最小负数(即绝对值最大)与最大正数的乘积)
public int maximumProduct(int[] nums) {
public int maximumProduct(int[] nums) {
Arrays.sort(nums);
int n = nums.length;
return Math.max(nums[0] * nums[1] * nums[n - 1], nums[n - 3] * nums[n - 2] * nums[n - 1]);
}
}
238.除自身以外数组的乘积
如果可以使用除法,只需要全部的数字乘起来再除以当前数字即可
唯一的难点就是不能使用除法,且时间复杂度是O(n)
使用左右两边的遍历方法
1 2 3 4
左边乘积 1 1 1*2 1*2*3
右边乘积 2*3*4 3*4 4 1
那么答案就变成了当前数字的左边乘积*当前数字的右边乘积
public int[] productExceptSelf(int[] nums) {
int length = nums.length;
int[] result = new int[length];
//获取左边的乘积
int[] left = new int[length];
left[0] = 1;
for (int i = 1; i < length; i++) {
left[i] = left[i-1]*nums[i-1];
}
//结果的最后一个数字等于left最后一个数字的值
result[length-1] = left[length-1];
int rightMul = 1;
for (int j = length-2; j >= 0; j--) {
//rightMul来记录当前数字右边的乘积值
rightMul = rightMul*nums[j+1];
result[j] = rightMul*left[j];
}
return result;
}
统计数组中的元素
645.错误的集合
直接遍历,新建数组存储对每个存在的数字计数
则最后返回的是计数值为0和计数值为2的数组
利用下标0、1、2、3、4的数组存放数字1、2、3、4的数量
public int[] findErrorNums(int[] nums) {
int[] countArray = new int[nums.length];
for (int i=0;i<nums.length;i++){
//例如当前取出的第i=3个数字为nums[3]=6
//那么在新的数组中存储的位置就是j=nums[3]=5
//因为存在重复的数字,所以要把原来的计数值加上
countArray[nums[i]-1] = 1+countArray[nums[i]-1];
}
int wrong = 0;
int correct = 0;
for (int j = 0;j<countArray.length;j++){
if (countArray[j]==2){
wrong = j+1;
}
if (countArray[j]==0){
correct = j+1;
}
}
return new int[]{wrong,correct};
}
448.找到所有数组中消失的数字
排序后计数,计数值为0的即为缺少的数字
public List<Integer> findDisappearedNumbers(int[] nums) {
Arrays.sort(nums);
int[] countArray = new int[nums.length];
for (int i=0;i<nums.length;i++){
//例如当前取出的第i=3个数字为nums[3]=6,那么在新的数组中存储的位置就是j=nums[3]=5
//因为存在重复的数字,所以要把原来的计数值加上
countArray[nums[i]-1] = 1+countArray[nums[i]-1];
}
List<Integer> list = new ArrayList<>();
for (int j = 0; j<countArray.length;j++){
if (countArray[j]==0){
list.add(j+1);
}
}
return list;
}
442.数组中重复的数据
排序之后的数组和前一个数字进行比较,如果相同,计数加一
为了考虑只有一个元素的数组,前一个元素初始化为0
public List<Integer> findDuplicates(int[] nums) {
List<Integer> list = new ArrayList<>();
for (int i = 0; i < nums.length; i++) {
int index = Math.abs(nums[i])-1;
int numIndex = nums[index];
if (numIndex>0){
nums[index] = -numIndex;
}else {
list.add(index+1);
}
}
return list;
}
41.缺失的第一个正数
难点在于不能申请新的数组
可以遍历数组,将在1-n范围中的数字放到(swap交换操作)正确的下标位置上
比如数字3放到物理上的第三个位置,即下标为2的位置
只要交换过来的数字不是正确数字(即num[i]=i-1)或者超出1-n的范围
则继续swap交换,直到满足条件
最后只需要找出第一个不在1-n范围内的数字下标i+1,即为缺失的数字(例如数组[1,2,9,4],缺失3)
否则就是数组长度+1(例如数组[1,2,3,4],缺失5)
// [3,4,-1,1]
public int firstMissingPositive(int[] nums) {
int length = nums.length;
for (int i = 0; i < length; i++) {
re:while (nums[i]>=1 && nums[i]<length+1){
if (nums[i]!=i+1){
swap(nums,i,nums[i]-1);
//如果在数组范围中,并且在自己的位置,则退出循环
if (nums[i]>=1 && nums[i]<length+1 && nums[i]==nums[nums[i]-1]){
break ;
}else {
//再次回到判断
continue re;
}
}else {
break;
}
}
}
int result = length+1;
for (int j = 0; j < length; j++) {
if (nums[j]!=j+1){
result = j+1;
break;
}
}
return result;
}
//需要交换的数组,源下标,目的下标
public void swap(int[] nums,int source,int destination){
nums[source] = nums[source]^nums[destination];
nums[destination] = nums[source]^nums[destination];
nums[source] = nums[source]^nums[destination];
}
数组的移动和改变
453.最小操作次数使数组元素相等
思维特别重要:
- 每个操作后n-1个数字会加一
- 反过来想就是其中最大的一个数字减一
- 即计算所有的数字减到最小的数字所花的次数(两个数的差值)
public int minMoves(int[] nums) {
IntStream stream = Arrays.stream(nums);
int minNum = stream.min().getAsInt();
int result = 0;
for (int i = 0; i < nums.length; i++) {
result = result + nums[i]-minNum;
}
return result;
}
665.非递减数列
看下面的几个测试用例,它们都因为数字 2 的出现,导致数组是非单调递增的。
例①: 4, 2, 5
例②: 1, 4, 2, 5
例③: 3, 4, 2, 5
当数组中出现 2 时,破坏了数组的单调递增。为了让数组有序,我们需要对 2 或者 4 进行调整:
第①个用例,我们可以 把 4 调小到 <= 2 或者 把 2 调大到 4、5 ,使数组有序。
第②个用例,我们可以 把 4 调小到 1、2 或者 把 2 调大到 4、5 ,使数组有序。
第③个用例,我们必须 把 2 调大到 4、5,才能使数组有序:我们不能把 4 调整为一个 <= 2 的数字,因为 4 前面的元素是 3.
总结:
当 nums[i] 破坏了数组的单调递增时,即nums[i]<nums[i - 1] 时,为了让数组有序,我们发现一个规律(在上面三个例子中, nums[i] 都为 2, nums[i -1] 都为 4):
- 如例①的情况,当
i = 1,那么修改num[i- 1],不要动nums[i],因为nums[i]后面的元素是啥我们还不知道呢,少动它为妙。 - 如例②的情况,当
i > 1时,我们应该优先考虑把nums[i - 1]调小到>= nums[i - 2]并且<= nums[i]。同样尽量不去修改nums[i],理由同上。 - 如例③的情况,当
i > 1且nums[i] < nums[i - 2]时,我们无法调整nums[i - 1],我们只能调整nums[i]到nums[i - 1]。
public boolean checkPossibility(int[] nums) {
if (nums == null || nums.length <= 1) {
return true;
}
int cnt = 0;
for (int i = 1; i < nums.length && cnt < 2; i++) {
if (nums[i-1] <= nums[i]) {
continue;
}
cnt++;
if (i-2>=0 && nums[i-2] > nums[i]) {
nums[i] = nums[i-1];
}else {
nums[i-1] = nums[i];
}
}
return cnt <= 1;
}
283.移动零
应用两个指针i和j
num[i]用来遍历,num[j]用来记录当前为0的元素
每当i遍历到非0的元素,就将当前元素和j所代表的元素进行交换,同时j+1指向下一个元素
因为i每次都是到非零元素才交换,所以除了自身和自身的交换(此时i和j同步)
到了0元素的位置不交换,i往下移动,但是j不移动,意味着j一定能移动到0的位置
此后,一直循环即可
public void moveZeroes(int[] nums) {
int zeroIndex = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i]!=0){
swap(nums,i,zeroIndex);
//每次交换之后,zeroIndex就移动到了下一个位置
zeroIndex++;
}
}
}
public void swap(int[] num,int i,int j){
int temp = num[i];
num[i] = num[j];
num[j] = temp;
}
二维数组
118.杨辉三角
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> listOut = new ArrayList<>();
for (int i=0;i<numRows;i++){
if (i==0){
ArrayList<Integer> list1 = new ArrayList<>();
list1.add(1);
listOut.add(list1);
}else if (i==1){
ArrayList<Integer> list2 = new ArrayList<>();
list2.add(1);
list2.add(1);
listOut.add(list2);
}else {
//第i行有i+1个数字
ArrayList<Integer> list3 = new ArrayList<>();
for (int j = 0; j < i+1; j++) {
//我需要获取上一行的数组,为i-1
List<Integer> lastList = listOut.get(i - 1);
if (j==0 || j==i){
list3.add(1);
}else {
int pre = lastList.get(j-1);
int next = lastList.get(j);
list3.add(pre+next);
}
}
listOut.add(list3);
}
}
return listOut;
}
119.杨辉三角Ⅱ
public List<Integer> getRow(int rowIndex) {
List<List<Integer>> listOut = new ArrayList<>();
for (int i=0;i<rowIndex+1;i++){
if (i==0){
ArrayList<Integer> list1 = new ArrayList<>();
list1.add(1);
listOut.add(list1);
}else if (i==1){
ArrayList<Integer> list2 = new ArrayList<>();
list2.add(1);
list2.add(1);
listOut.add(list2);
}else {
//第i行有i+1个数字
ArrayList<Integer> list3 = new ArrayList<>();
for (int j = 0; j < i+1; j++) {
//我需要获取上一行的数组,为i-1
List<Integer> lastList = listOut.get(i - 1);
if (j==0 || j==i){
list3.add(1);
}else {
int pre = lastList.get(j-1);
int next = lastList.get(j);
list3.add(pre+next);
}
}
listOut.add(list3);
}
}
return listOut.get(listOut.size()-1);
}
数组的旋转
189.轮转数组
该方法为数组的翻转:我们可以先将所有元素翻转,这样尾部的 k mod n 个元素就被移至数组头部,然后我们再翻转 [0, k mod n-1] 区间的元素和 [k mod n, n-1]区间的元素能得到最后的答案。
我们以 n=7,k=3 为例进行如下展示:
| 操作 | 结果 |
|---|---|
| 原始数组 | 1 2 3 4 5 6 7 |
| 翻转所有元素 | 7 6 5 4 3 2 1 |
翻转 [0, k mod n - 1] 区间的元素 |
5 6 7 4 3 2 1 |
翻转 [k mod n, n-1]区间的元素 |
5 6 7 1 2 3 4 |
public void rotate(int[] nums, int k) {
k %= nums.length;
reverse(nums, 0, nums.length - 1);
reverse(nums, 0, k - 1);
reverse(nums, k, nums.length - 1);
}
public void reverse(int[] nums, int start, int end) {
while (start < end) {
int temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
start += 1;
end -= 1;
}
}
396.旋转函数
类似于旋转数组,计算当前数组的最大值之后进行旋转,利用max存储当前的最大值,反复迭代
//最后求出其中的最大值
public int maxRotateFunction(int[] nums) {
int max = 0;
//设置move为移动的次数,总共可以移动数组长度-1次
for (int move = 0; move < nums.length; move++) {
//计算当前的值
int now = 0;
for (int i = 0; i < nums.length; i++) {
now += i*nums[i];
}
max = Math.max(max,now);
//全部反转
turn(nums,0,nums.length-1);
//然后调换1到最后的nums.length-1个数字即可
turn(nums,1,nums.length-1);
}
return max;
}
public void turn(int[] nums,int start,int end){
while (start<end){
int temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
start++;
end--;
}
}
遍历特殊的数组
54.螺旋矩阵
利用left,right,top和bottom四个变量记录当前的位置,每当遍历完一行或者一列,四个变量进行相应的变换(增加或者减少来标识当前已经被遍历过)
public List<Integer> spiralOrder(int[][] matrix) {
ArrayList list = new ArrayList();
if (matrix.length==0){
return list;
}
//获得行长度、列长度
int length = matrix.length;
int width = matrix[0].length;
//整个数组的数字个数
int numCount = length*width;
//记录遍历的指针上下左右的大小
int left=0,right=width-1,top=0,bottom=length-1;
//记录遍历了的数字个数
int forNumCount = 0;
while (forNumCount<numCount){
//从左到右遍历最上一行
//每次遍历的时候必须判断是否已经遍历完了全部的数字
//因为四轮为一次遍历,中间就可能已经遍历完了,需要退出循环
for (int i = left;i <= right && forNumCount<numCount;i++){
int nowNum = matrix[top][i];
list.add(nowNum);
//遍历的数字加一
forNumCount++;
}
//遍历完一行,top计数加一,表示少了一行
top++;
//从上到下遍历右边一列
for (int j = top; j <= bottom && forNumCount<numCount; j++) {
int nowNum = matrix[j][right];
list.add(nowNum);
//遍历的数字加一
forNumCount++;
}
//遍历完一列,right计数减一,表示少了一列
right--;
//从右到左遍历底部一行
for (int m = right; m >= left && forNumCount<numCount; m--) {
int nowNum = matrix[bottom][m];
list.add(nowNum);
forNumCount++;
}
//遍历完一行,bottom计数加一,表示少了一行
bottom--;
//从下到上遍历左边一列
for (int n = bottom; n >= top && forNumCount<numCount; n--) {
int nowNum = matrix[n][left];
list.add(nowNum);
forNumCount++;
}
//遍历完一列,left计数加一,表示少了一列
left++;
}
return list;
}
59.螺旋矩阵Ⅱ
直接类似于上一个螺旋矩阵,但是只是需要往里面赋值
public int[][] generateMatrix(int n) {
int[][] result = new int[n][n];
//总的数字个数和遍历的数字个数
int sumNumCount = n*n, forNumCount = 1;
int left=0,right=n-1,top=0,bottom=n-1;
while (forNumCount<=sumNumCount){
for (int i = left; i <= right && forNumCount<=sumNumCount; i++) {
result[top][i] = forNumCount;
forNumCount++;
}
top++;
for (int i = top; i <= bottom && forNumCount<=sumNumCount; i++) {
result[i][right] = forNumCount;
forNumCount++;
}
right--;
for (int i = right; i >= left && forNumCount<=sumNumCount; i--) {
result[bottom][i] = forNumCount;
forNumCount++;
}
bottom--;
for (int i = bottom; i >= top && forNumCount<=sumNumCount; i--) {
result[i][left] = forNumCount;
forNumCount++;
}
left++;
}
return result;
}
二维数组变换
566.重塑矩阵
我们最笨的方法可以把数组全部取出来,再放到新的数组中
但是同时,我们可以不遍历原数组
如果从起始位置算为0,我们可以将任意纬度的数组转化为一个一维数组
对于原数组 m*n 的数组,当前数字的遍历角标为des(0,1,2,3,4……m*n),则0<=des<=m*n
数字在原数组 m*n中的位置:x=des/c,y=des%c,即 mat[des/n][des%n]
则在新的 r*c 数组中所在的位置是:x=des/c,y=des%c,即result[des/c][des%c]
public int[][] matrixReshape(int[][] mat, int r, int c) {
int width = mat[0].length;
int sumNumCount = mat.length*width;
//数字的数量
int dest = 0;
int[][] result = new int[r][c];
if (r*c!=sumNumCount){
return mat;
}else {
while (dest<sumNumCount){
result[dest/c][dest%c] = mat[dest/width][dest%width];
dest++;
}
return result;
}
}
48.旋转图像
设行为length,列为width,旋转之后图形设置为result
我们的第i行元素旋转之后都在倒数第i列
意味着 result[j][width-1-i] =matrix[i][j](因为是数组,所以还要减一)
但是因为是四边形,所以无论如何旋转都只要四次临时变量即可
官网解释
public void rotate(int[][] matrix) {
//标记是n*n的矩阵
int n = matrix.length;
//旋转的次数是矩阵纬度
for (int i = 0; i < n / 2; ++i) {
for (int j = 0; j < (n + 1) / 2; ++j) {
int temp = matrix[i][j];
matrix[i][j] = matrix[n - j - 1][i];
matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
matrix[j][n - i - 1] = temp;
}
}
}
73.矩阵置零
记录每一行的0所在的行和列,最后再遍历置零
public void setZeroes(int[][] matrix) {
Set<Integer> rowSet = new HashSet<>();
Set<Integer> colSet = new HashSet<>();
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[i].length; j++) {
if (matrix[i][j]==0){
rowSet.add(i);
colSet.add(j);
}
}
}
for (Integer row:rowSet) {
rowZero(matrix,row);
}
for (Integer col:colSet) {
colZero(matrix,col);
}
}
//把某一行全部置零
public void rowZero(int[][] arr,int row){
int width = arr[0].length;
for (int i = 0; i < width; i++) {
arr[row][i] = 0;
}
}
//把某一列全部置零
public void colZero(int[][] arr,int col){
int length = arr.length;
for (int i = 0; i < length; i++) {
arr[i][col] = 0;
}
}
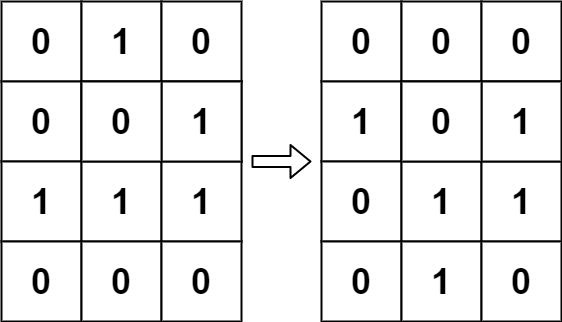
289.生命游戏
堪称目前为止写到的脑洞最大的题目之一
首先是初始状态判定
为了保证当前修改后的状态不会影响下一个状态的判定,设置另外的状态
如题所示,只有三种:
-
如果当前是活细胞,但是变成了死细胞,那么设置为-1
-
如果当前是活细胞,仍然是活细胞,那么不变仍为1
-
如果当前是死细胞,但是变成了活细胞,那么设置为2
那么最后遍历修改完状态之后,将-1修改回为0,2修改回为1
其次是如何遍历出某个节点周围的所有节点
当前节点是[ i , j ]
[i-1,j-1] [i-1,j] [i-1,j+1]
[ i ,j-1] [ i ,j] [ i ,j+1]
[i+1,j-1] [i+1,j] [i+1,j+1]
那么以当前节点为中心,要求周围的节点,则最多是3*3形式
所以我们利用两个for循环,形成遍历
并且所有的行和列都是用当前节点+1或者-1或者不变构成
所以我们设置 ner = {-1,0,1} ,形成方向
接着是如何表示当前节点周围有多少存活的细胞
判断当前周围节点的存活状态,要求满足两个状态:
- 必须保证要在 board 矩阵中
- 并且起始状态要是存活,则当前状态为1或者-1都可以(因为这两个状态都表示起始状态为活细胞)
最后是形成下一个状态
开始判断当前节点的存活状态
要注意:因为遍历到当前节点的时候,还没有开始修改细胞状态,所以还是0和1的细胞状态
那么只需要判断状态变化的即可,否则状态不变
public void gameOfLife(int[][] board) {
//设置方向来遍历某个节点周围的另外几个节点
int[] ner = new int[]{-1,0,1};
//获取行和列
int rows = board.length;
int cols = board[0].length;
//遍历每一个节点格子
for (int row = 0; row < rows; row++) {
for (int col = 0; col < cols; col++) {
//设置当前节点周围的存活细胞的数量
int liveNer = 0;
//开始遍历周围的节点
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
//必须保证不计算当前节点(不计算自己)
if (!(ner[i]==0 && ner[j]==0)){
//当前节点的相邻节点坐标
int r = row+ner[i];
int c = col+ner[j];
//计算有多少存活的细胞
if ((r>=0&&r<rows) && (c>=0&&c<cols)
&& (Math.abs(board[r][c])==1)){
liveNer++;
}
}
}
}
if ((board[row][col]==1) && ( liveNer>3 || liveNer<2)){
// -1 代表这个细胞过去是活的现在死了
board[row][col]=-1;
}
if (board[row][col]==0 && ( liveNer==3)){
// 2 代表这个细胞过去是死的现在活了
board[row][col]=2;
}
}
}
//再把额外的状态修改回去
for (int row = 0; row < rows; row++) {
for (int col = 0; col < cols; col++) {
if (board[row][col] == 2) {
board[row][col] = 1;
}
if (board[row][col] == -1){
board[row][col] = 0;
}
}
}
}