正则化与正则剪枝
写在前面:本博客仅作记录学习之用,部分图片来自网络,如需引用请注明出处,同时如有侵犯您的权益,请联系删除!
文章目录
- 引言
- 正则化
-
- 为什么会过拟合
- 拉格朗日与正则化
- 梯度衰减与正则化
- 应用
-
- 解决过拟合
- 网络剪枝
- 总结
- 致谢
- 参考
引言
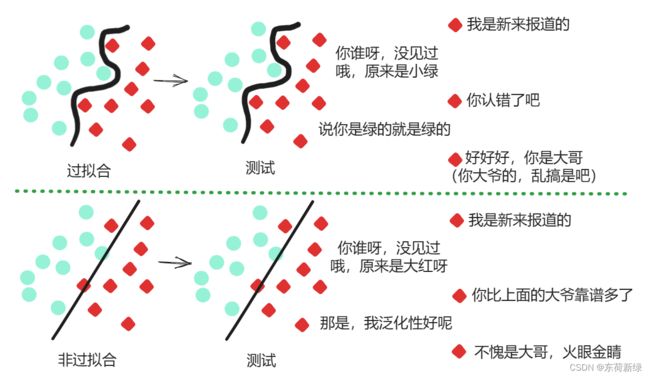
在深度学习中,模型的复杂度通常是由模型参数的数量和取值范围来决定的。当模型太过复杂时,容易过拟合,即训练集上表现很好,测试集上表现较差,原因在于模型过于适应训练集数据或训练数据过少,从而导致泛化能力不足,如下图。
训练模型本质上是从子集推广到全集,不论是子集太少不足以近似描述全集的性质,还是过分信任子集,即把子集当作全集,在测试全集中的数据表现都不佳。
减少过拟合的方法和技术有很多,下面列举了一些常用的方法:
- 数据增强(Data Augmentation): 通过对训练集中的数据进行随机变换、旋转、缩放等操作,生成更多的样本以拟合训练全集的数据分布,帮助模型更好地泛化。
- 正则化(Regularization): 通过在损失函数中引入正则化项,控制模型的复杂度,防止模型过度拟合,常见的正则化方法有L1正则化和L2正则化。
- Early Stopping: 在训练过程中,监控模型在验证集上的性能指标。当模型在验证集上的性能不再提升时,停止训练,以避免过拟合。
- Dropout/DropBlock: 在训练过程中,随机丢弃一部分神经元的输出,以减少神经网络中神经元之间的依赖关系,从而降低过拟合风险。
- 权重衰减(Weight Decay): 在优化算法中,对模型的权重进行衰减(即乘以一个小于1的因子),以限制权重的增长,减少模型的复杂度。
- 简化模型结构: 减少模型的参数量和复杂度,例如减少隐藏层的数量、减少神经元的数量,以降低过拟合的可能性。
以上方法基本上是通过扩大训练的子集、或使网络稀疏降低网络的拟合能力、约束网络参数,以提高网络泛化能力。正则化的意义不仅仅在于提高模型的泛化能力,使其在面对新数据时能够更好地表现,同时正则化在网络剪枝方面也有应用。
正则化
为什么会过拟合
对于卷积或者全连接之类的线性操作,可以简单表示为 y = x × W + b y = x \times W + b y=x×W+b,w是权重,b是偏置。对于多层线性操作 y = f ( . . . f ( x ) ) y = f(...f(x)) y=f(...f(x)), f ( x i ) = x i × W i + b i f(x_i) = x_i \times W_i + b_i f(xi)=xi×Wi+bi,不妨考虑极端情况所有偏置为0,多层线性操作 y = f ( . . . f ( x ) ) = x × W 1 × W 2 × . . . × W n y = f(...f(x)) = x \times W_1\times W_2\times...\times W_n y=f(...f(x))=x×W1×W2×...×Wn,对于一个特定的输出y,其参数的可能组合有无数种,更何况还有偏置以及非线性的激活函数,网络的拟合能力就更强。
因此对于有限的训练集,网络完全可以记住所有样本的对应的结果导致泛化性差。不难想到降低权重和偏置数量不就可以降低网络的拟合能力,确实是这样。简化网络结构或者使用drop操作,可以减少网络参数或者降低有效的参数的数量达到减少过拟合的情况。此外网络参数的数据类型多是float32,在不加约束的情况下,网络参数不仅组合多并且可能会很大,参数过大会放大输入中的噪声和错误信息进而导致错误结果,参数约束后可以减少输入的中一些干扰,确保泛化性。
拉格朗日与正则化
正则化就是约束网络参数的一种经典方法,通过在模型训练过程中引入惩罚项来控制模型的复杂度,从而避免过拟合现象。在正则化中,常见的惩罚项有L1正则化和L2正则化。L1正则化将模型参数的绝对值之和作为惩罚项,促使模型参数中的某些维度变为0,从而实现特征选择的效果;L2正则化将模型参数的平方和作为惩罚项,促使参数的值尽可能小,从而防止模型过于复杂,这里主要是指对参数W的正则化,过拟合的来源主要也是W,不考虑偏置是因为偏置只是平移的功能。
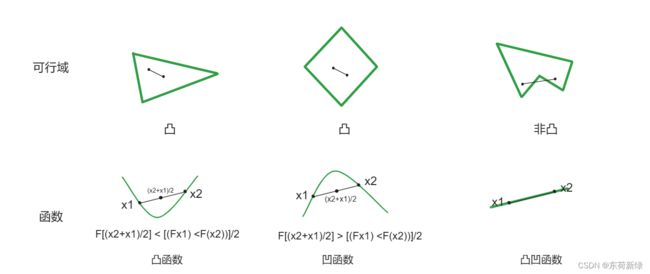
L1、L2正则化中的正则项主要利用L1、L2范数,其实是计算该位置和原点的位置,把勾股定理推理到高维即可。如下,计算高维参数和原点的曼哈顿距离和欧氏距离,相同的范数的点连接起来就是一个正方形和圆,在 p p p 大于等于1 时,此时的可行域是凸集(凸集:该区域内任意两点的连线都在该区域内)。
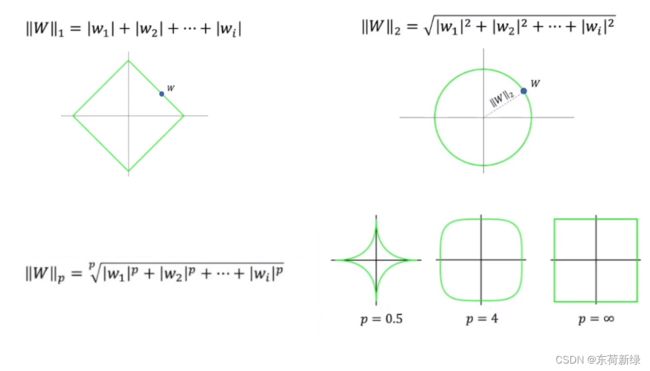
不妨假设损失函数为 L o s s = J ( W , b ) Loss = J(W,b) Loss=J(W,b),上文说过b可不进一步约束,因此 L o s s = J ( W ) Loss = J(W) Loss=J(W)。对于损失函数,不妨规定可行域,即 ∣ ∣ W ∣ ∣ 1 − C ≤ 0 ||W||_1 - C \leq 0 ∣∣W∣∣1−C≤0,C是约束条件,让W都在该较小的范围内,进而损失函数的拉格朗日表达式可变为 L o s s ( W , λ ) = J ( W ) + λ ( ∣ ∣ W ∣ ∣ 1 − C ) Loss(W,\lambda) = J(W)+\lambda(||W||_1 - C) Loss(W,λ)=J(W)+λ(∣∣W∣∣1−C),其中 λ ≥ 0 \lambda\geq0 λ≥0。同理当可行域为 ∣ ∣ W ∣ ∣ 2 − C ≤ 0 ||W||_2 - C \leq 0 ∣∣W∣∣2−C≤0,进而损失函数可变为 L o s s ( W , λ ) = J ( W ) + λ ( ∣ ∣ W ∣ ∣ 2 − C ) Loss(W,\lambda) = J(W)+\lambda(||W||_2 - C) Loss(W,λ)=J(W)+λ(∣∣W∣∣2−C),图像的表达形式如下:

以二维示例或理解为高维空间在二维上的投影,越靠近等高线的中心,损失越小,其中在交点处就是所求的最值点,因为对于优化问题而言(因为 ∣ ∣ W ∣ ∣ 1 ∣ ||W||_1| ∣∣W∣∣1∣, ∣ ∣ W ∣ ∣ 2 ∣ ||W||_2| ∣∣W∣∣2∣的可行域是凸集( p ≥ 1 p\geq1 p≥1)不改变求解问题的凹凸性),最值点需要满足导数或梯度为0,因此只有在 ∣ ∣ W ∣ ∣ 1 ∣ ||W||_1| ∣∣W∣∣1∣的顶点与 ∣ W ∣ ∣ 2 |W||_2 ∣W∣∣2切点处,才能满足梯度为零的条件,如下图。
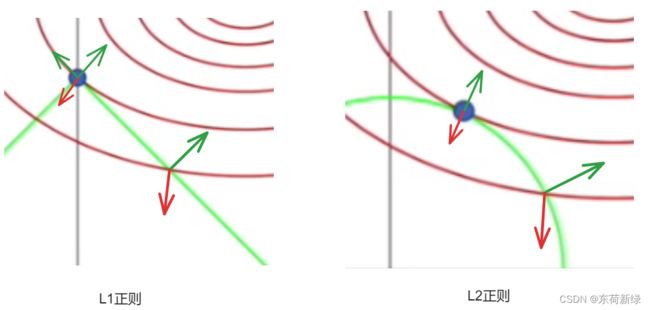
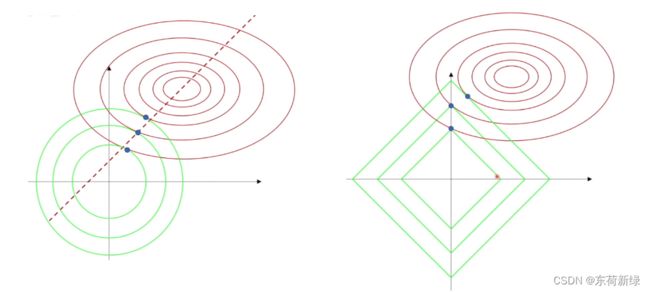
对于不同的C值,具有不同的可行域。可以看到, ∣ ∣ W ∣ ∣ 1 ||W||_1 ∣∣W∣∣1正则化取极值的点有些在坐标轴上,因此会使得网络部分参数是0,进而达到稀疏网络或者说特征选择的作用。相反 ∣ ∣ W ∣ ∣ 2 ||W||_2 ∣∣W∣∣2一般不会在坐标轴上,不具备稀疏网络的作用。举个不恰当的例子, ∣ W ∣ |W| ∣W∣求导之后是+1或者-1,因此无论W在那个位置,梯度下降的速度是比较快的,因此总会有些W为0。 W 2 W^2 W2求导之后是2W,W越接近0,梯度越来越小,越来越走不动。因此W只会密集的接近0而不会是0,因此没有稀疏作用。
梯度衰减与正则化
从求解过程来说,只要保证梯度为0即可,因此可去除常数C,会导致极值不一样,但是取得极值的w是一样的,即 L o s s ( W , λ ) = J ( W ) + λ ⋅ ∣ ∣ W ∣ ∣ 1 Loss(W,\lambda) = J(W)+\lambda\cdot||W||_1 Loss(W,λ)=J(W)+λ⋅∣∣W∣∣1或者 L o s s ( W , λ ) = J ( W ) + λ ⋅ ∣ ∣ W ∣ ∣ 2 Loss(W,\lambda) = J(W)+\lambda\cdot||W||_2 Loss(W,λ)=J(W)+λ⋅∣∣W∣∣2,这就是常见的对损失函数的约束, λ \lambda λ通常是保证在极值处梯度总和为0,因此定下来 λ \lambda λ 就等于确定了极值点的位置。
再次的给出损失 L = J ( W ) L = J(W) L=J(W),权重更新的方式: W = W − η ⋅ ∇ w ⋅ J ( W ) W= W-\eta\cdot\nabla_w\cdot J(W) W=W−η⋅∇w⋅J(W), η \eta η 为学习率;
正则化后 L = J ( W ) + λ ⋅ ∣ ∣ W ∣ ∣ 2 L = J(W) + \lambda \cdot ||W||_2 L=J(W)+λ⋅∣∣W∣∣2,对于实际的 ∣ ∣ W ∣ ∣ 2 ||W||_2 ∣∣W∣∣2计算,对于高维向量各项的平方和可表示为 W T W W^TW WTW 并且开方运算计算量较大,开方运算不影响函数的单调性,因此使用 W T W W^TW WTW来等价 ∣ ∣ W ∣ ∣ 2 ||W||_2 ∣∣W∣∣2即可。因此可 L ^ = J ( W ) + α 2 ⋅ W T W \hat{L }= J(W) + \frac {\alpha} {2} \cdot W^TW L^=J(W)+2α⋅WTW,分母2为了抵消平方的求导的系数。
权重更新需要加上正则化项: W = W − η ⋅ ∇ w ⋅ J ( W ) − η ⋅ α ⋅ W W= W-\eta \cdot \nabla_w \cdot J(W)-\eta \cdot \alpha \cdot W W=W−η⋅∇w⋅J(W)−η⋅α⋅W = ( 1 − η ⋅ α ) W − η ⋅ ∇ w ⋅ J ( W ) (1-\eta \cdot \alpha) W -\eta \cdot \nabla_w \cdot J(W) (1−η⋅α)W−η⋅∇w⋅J(W),在 ( 1 − η ⋅ α ) (1-\eta \cdot \alpha) (1−η⋅α)在[0,1]之间时候,W在每次更新的时候都会衰减,这也是为什么L2正则化也叫做权重衰减,随着更新次数增多,W可改变的范围越来越小,也就是上文所提到的不恰当的例子中越来越走不动的原因。
不妨假设神经网络的函数为 f ( x ) f(x) f(x),过拟合即是 f ( x ) f(x) f(x)可产生区分每个训练样本的分界线,分界线会多次转折或弯曲去区分,可参考第一个图中的黑色线。通过将 f ( x ) f(x) f(x)展开为泰勒公式则有: f ( x ) = f ( a ) + f ′ ( a 0 ) ( x − a 0 ) + 1 2 f ′ ′ ( a 0 ) ( x − a 0 ) 2 + ⋅ ⋅ ⋅ + 1 2 f ( n ) ( a 0 ) ( x − a 0 ) n f(x) = f(a) + f'(a_0)(x-a_0) + \frac {1} {2}f''(a_0)(x-a_0)^2 + \cdot \cdot\cdot + \frac {1} {2}f^{(n)}(a_0)(x-a_0)^n f(x)=f(a)+f′(a0)(x−a0)+21f′′(a0)(x−a0)2+⋅⋅⋅+21f(n)(a0)(x−a0)n ,通过控制高次项的系数趋于0,就可降低 f ( x ) f(x) f(x) 拟合能力(减少分界线的转折次数或程度),即控制W趋于0, f ( n ) ( a 0 ) f^{(n)}(a_0) f(n)(a0)也得趋于0,在 f ( n ) ( a 0 ) f^{(n)}(a_0) f(n)(a0)趋于0时,只惩罚大于1的高次项。
此外正则化去除常数C,会导致极值不一样,但是这个极值的误差到底有多大,这是需要关注的,在此不妨假设 J ( W ∗ ) J(W^*) J(W∗), J ( W ^ ) J(\hat{W}) J(W^) 分别是正则化前后的极值, W ∗ W^* W∗, W ^ \hat{W} W^是其取得极值的权重,在这里直接截取了L1和L2正则化”直观理解(之二)的内容,对于L1一般Hessian矩阵无法得到清晰的表达式,此处略过,近似的方法参考该视频第24:00分钟的内容。
本质上,L1正则化、L2正则化就是在不同的 α \alpha α下对权重进行缩放,L1正则化的结果如下:

应用
解决过拟合
上文已经叙述了L1正则化,L2正则化对网络权重的约束,包括稀疏和权重衰减,此处简单示例如何使用L1正则化,L2正则化
import torch
import torch.nn as nn
# 定义模型
model = nn.Linear(10, 1) # 以一个简单的线性模型为例
# 创建一些随机输入
input = torch.randn(5, 10)
# 获取模型的权重参数
parameters = model.parameters()
weights = [param for name, param in parameters]
# 计算L1正则化
l1_regularization = torch.tensor(0.)
for weight in weights:
l1_regularization += torch.sum(torch.abs(weight))
# 计算L2正则化
l2_regularization = torch.tensor(0.)
for weight in weights:
l2_regularization += torch.sum(weight**2)
# 设置正则化系数
l1_lambda = 0.01
l2_lambda = 0.01
# 将正则化项添加到损失函数中
criterion = nn.MSELoss() # 以均方误差作为损失函数为例
loss = criterion(model(input), torch.randn(5, 1))
loss += l1_lambda * l1_regularization
# 或者
# loss += l2_lambda * l2_regularization
# 进行反向传播等其他训练步骤...
网络剪枝
除了对网络的参数进行正则化,其实也有一些应用在剪枝,其目的就是通过正则化后的权重来评估通道的贡献度,贡献度很小的通道(小的W就可以省略进行剪枝)。

Slimming: Learning Efficient Convolutional Networks through Network Slimming
论文速递: 点击转跳
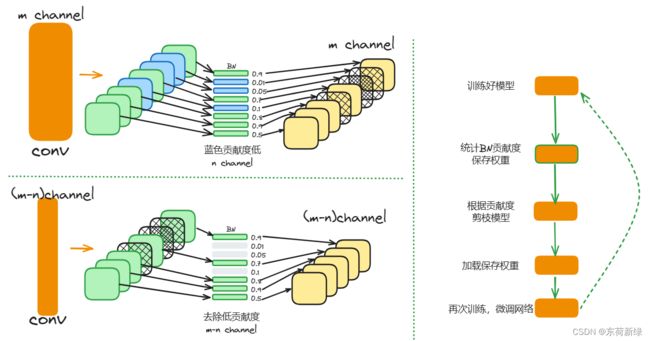
利用BN层的比例因子: 为每个通道引入一个缩放因子γ,乘以该通道的输出。然后联合训练网络权值和这些比例因子,并对后者进行稀疏正则化。最后对这些小因子频道进行修剪,并对修剪后的网络进行微调。通常卷积和BN会一起使用,结合BN标准化激活的方式设计有效的方法来结合通道尺度因子。BN层使用小批量统计对内部激活进行规范化。设 z i n 和 z o u t z_{in}和z_{out} zin和zout分别为BN层的输入和输出,B表示当前的mini-batch, BN层进行如下变换:

其中 µ B , σ B µ_B,σ_B µB,σB是B上输入激活的平均值和标准差值,γ和β是可训练的仿射变换参数(尺度和位移)。
具体来说,训练目标由损失函数和正则化项组成。
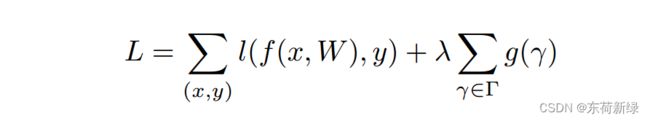
其中(x, y)表示训练输入和目标,W表示可训练权值,第一个求和项对应于网络的正常训练损失,g(·)是缩放因子上的稀疏性惩罚,λ平衡这两项。常见的使用L1/L2正则化,使得其中的缩放因子趋于0.
由于修剪通道本质上相当于删除该通道的所有传入和传出连接,比例因子作为渠道选择的代理。与网络权值共同优化,自动识别不重要的信道,可以在不影响泛化性能的情况下安全地去除不重要的信道。通过去除所有的进出连接和相应的权值来修剪比例因子接近于零的信道来更紧凑的网络,具有更少的参数和运行时内存,以及更少的计算操作。
当剪枝比较高时,剪枝可能会暂时导致一些精度损失。在很大程度上可以通过在修剪后的网络上进行随后的微调过程来补偿,如下图的虚线。
通过对批归一化层的比例因子施加稀疏性诱导的正则化,在训练过程中自动识别不重要的通道并进行修剪,能够显着降低最先进网络的计算成本(高达20倍),而没有准确性损失。该方法同时减少了模型大小、运行时内存和计算操作,同时在训练过程中引入了最小的开销,并且所得到的模型不需要特殊的库/硬件来进行有效的推理。
总结
正则化是一种在机器学习中用于控制模型复杂度的技术,它通过在损失函数中添加一个额外项来对参数进行约束,从而避免过拟合。其中,L1正则化通过对参数的绝对值求和来实现,能够产生稀疏权重;L2正则化通过对参数的平方和求根号来实现,能够产生较为平滑的权重;实际上可以结合两者来共同约束参数。
在实际应用中,正则化可以帮助模型更好地泛化数据,提高模型的鲁棒性和可靠性。同时,正则化也需要根据具体问题进行调整,不同的正则化方法和系数可能会产生不同的效果。正则化的意义不仅仅在于提高模型的泛化能力,使其在面对新数据时能够更好地表现,同时正则化在网络剪枝方面也有应用。
致谢
欲尽善本文,因所视短浅,怎奈所书皆是瞽言蒭议。行文至此,诚向予助与余者致以谢意。
参考
[1]. L1和L2正则化”直观理解(之二)
[2]. Liu Z, Li J, Shen Z, et al. Learning efficient convolutional networks through network slimming[C]//Proceedings of the IEEE international conference on computer vision. 2017: 2736-2744.