生成式深度学习(第二版)-译文-第七章-基于能量的模型
章节目标:
- 理解如何表述一个深度能量模型 (deep energy-based model, EBM)。
- 了解如何使用Langevin dynamics从 EBM中采样。
- 使用contrastive divergence训练你自己的EBM。
- 分析EBM,包括观察Langevin dynamics采样过程的快照。
- 了解其它类型的EBM,例如受限玻尔兹曼机。
基于能量的模型是一大类生成式模型,其核心思想借鉴自物理系统建模 — 也即,一个事件的概率可以用玻尔兹曼分布来表达,玻尔兹曼分布是一个将实值能量函数归一化到0-1之间的特殊函数。该分布于1868年由 Ludwig Boltzmann首度提出,他将之用于描述热均衡中的气态。
在本章中,我们将看看我们如何可以利用这一思想来训练一个可用于生成手写数字图像的生成式模型。我们也将探索几个新的概念,包括训练EBM的 contrastive divergence,以及用于采样的 Langevin dynamics。
引言
我们同样以一则简短的故事来介绍EBM背后的关键概念。
| Long-AU-VIN 跑步俱乐部 |
|---|
| Diane Mixx 是虚构的法国小镇 Long-au-Vin 上一家长跑俱乐部的头号教练。她因杰出的训练能力而远近闻名,并因为可以把平庸的运动员训练成世界级跑者收获了巨大声誉(图7-1)。 |
| 她的训练方法主要围绕对每个运动员能量水平的评估。常年与各种能力的运动员一起工作之后,她拥有了令人难以置信的精确直觉,可以在一场赛跑之后评估某个运动员还有多少能量剩余。一个运动员的能量水平越低,越好 — 杰出的运动员总是在比赛中竭尽全力。 |
| 为了保持自己的技能,她通过度量 自己关于知名精英运动员 和 本俱乐部优秀运动员 的能量感知能力对比 来经常性的训练自己。 她确保自己关于这两组运动员的预测发散度越大越好,使得人们充分信任她对于自己俱乐部杰出运动员的评估结果。 |
| 真正的魔力在于她善于把平庸跑者转变为顶尖跑者。过程是简单的 — 她度量运动员当前的能量水平,计算运动员下次改善水平所需的一组最优调整。然后,在进行这些调整之后,她再次度量运动员的能量水平,期待这次比之前更低,也就意味着运动表现在提升。这一评估最优调整+向正确方向进行小步调整的过程一直持续,直到运动员的水平最终与世界级运动员无差别为止。 |
| 很多年后,Diane从教练席退休,并出版了一本书介绍她培养精英运动员的方法 — 一个她称为"Long-au-Vin, Diane Mixx" 的技术。 |
Diane Mixx 和 Long-au-Vin 跑者俱乐部的故事揭示了基于能量模型背后的核心思想。让我们在正式用Keras实现实际例子之前,一起从细节上探索起理论。
基于能量的模型 (EBM)
基于能量的模型尝试用玻尔兹曼分布对真实的数据生成分布进行建模 (方程 7-1),其中 E ( x ) E(x) E(x) 是 观察 x x x 的能量函数 (或者 分数)。
p ( x ) = e − E ( x ) ∫ x ^ ∈ X e − E ( x ^ ) p(\mathbf{x}) = \frac{e^{-E(\mathbf{x})}}{\int_{\hat{x}\in \mathbf{X}}e^{-E(\hat{\mathbf{x}})}} p(x)=∫x^∈Xe−E(x^)e−E(x)
实操中,这意味着训练一个神经网络 E(x), 对于高可能观察,输出更低的score (也就意味着px 接近于1),对于不可能观察,输出更高的score (也就意味着px接近于0)。
用这种方式来建模数据有两大挑战。首先,如何使用模型来采样新观察并不清晰 — 我们可以用它对一个观察产生分数,但是如何在给定一个较低分数(也即一个可靠观察)的情况下生成一个观察呢?
其次,方程7-1的归一化分母包含了一个不易于处理的积分(除非是最简单的问题)。如果我们不能计算盖几份,那么我们不能使用最大化似然估计来训练模型,因为这要求 px 是一个有效的概率分布。
EBM模型背后的核心思想在于,我们可以使用近似技术来确保我们无需计算不易计算的分母。这与归一化流相反,在归一化流中,我们竭尽全力确保我们应用于标准高斯分布的变换不会改变输出仍然是有效概率分布的事实。
按照Du 和 Mordatch等在2019年论文 “Implicit Generation and Modeling with Energy-based Models.” 提出的思想。我们使用一项名为 contrastive divergence (训练) 和 一项名为 Langevin dynamics (采样) 的技术 来 技巧性绕过这个难解的分母问题。我们将从细节上探索这些技术,在本章稍后将构建我们自己的EBM。
首先,让我们构建一个数据集,并设计一个简单的神经网络来表示我们的实值能量函数 E(x)。
| 运行本例代码 |
|---|
| 本示例代码可以从本书附带代码库的以下路径找到:“notebooks/07_ebm/01_ebm/ebm.ipynb”, 该代码从 Phillip Lippe 的杰出 tutorial on deep energy-based generation models 修改而来。 |
MNIST 数据集
我们将用标准的MNIST数据集,包含手写数字的灰度图像。一些数据集的样例图如下图7-2所示。

数据集在TensorFlow中有预封装,可以按照样例7-1所示的方式来下载。
from tensorflow.keras import datasets
(x_train, _),(x_test, _) = datasets.mnist.load_data()
如之前一样,我们把像素值的范围放缩到 [-1, 1], 并在尺寸上加入一些填充使得图像为 32 x 32。我们进一步将它转换到 TensorFlow 数据集,如下样例7-2所示。
# 样例7-2 MNIST 数据集之预处理
def preprocess(imgs):
imgs = (imgs.astype("float32") - 127.5) / 127.5
imgs = np.pad(imgs, ((0,0),(2,2),(2,2)), constant_values = -1.0)
imgs = np.expand_dims(imgs, -1)
return imgs
x_train = preprocess(x_train)
x_test = preprocess(x_test)
x_train = tf.data.Dataset.from_tensor_slices(x_train).batch(128)
x_test = tf.data.Dataset.from_tensor_slices(x_test).batch(128)
既然我们已经有了自己的数据集,我们可以构建神经网络来表示能量函数 E ( x ) E(x) E(x)。
能量函数
能量函数 E θ ( x ) E_\theta(x) Eθ(x) 是一个参数为 θ \theta θ 的 神经网络,他可以将输入一张输入图像 x 转换为一个数值。通过这个网络,我们可以利用一个名为 swish 的激活函数,如下边栏所描述。
| Swish 激活函数 |
|---|
| Swish 是 谷歌在2017年引入的,作为 ReLU 的一个替代。其定义如下: |
| s w i s h ( x ) = x ⋅ s i g m o p i d ( x ) = x e ( − x ) + 1 swish(x) = x \cdot sigmopid(x) = \frac{x}{e^(-x)+1} swish(x)=x⋅sigmopid(x)=e(−x)+1x |
| swish视觉上比较接近ReLU,关键的区别在于它更平滑,可以帮助缓解梯度消失问题。这在能量模型中尤为重要。Swish函数的图像如图 7-3所示。 |

网络是一组堆叠的 Conv2D 层,可以逐渐减少图像尺寸,同时增加通道数。最后一层是一个单一的带线性激活的全连单元,因此网络可以输出的范围是 ( − ∞ , ∞ ) (-\infin,\infin) (−∞,∞)。可以构建的代码如下图7-3所示。
# 样例 7-3 构建神经网络的能量函数 E(x)
ebm_input = layers.Input(shape(32,32,1))
# 能量函数是一系列 Conv2D层的堆叠,激活函数是 swish 激活
x = layers.Conv2D(16, kernel_size=5, strides=2, padding="same", activation = activations.swish)(ebm_input)
x = layers.Conv2D(32, kernel_size=3, strides=2, padding="same", activation = activations.swish)(x)
x = layers.Conv2D(64, kernel_size=3, strides=2, padding="same", activation = activations.swish)(x)
x = layers.Conv2D(64, kernel_size=3, strides=2, padding="same", activation = activations.swish)(x)
x = layers.Flatten()(x)
x = layers.Dense(64, activation = activations.swish)(x)
# 最后一层是一个单一的全连层,线性激活函数
ebm_output = layers.Dense(1)(x)
# Keras 模型:将输入图像转换为一个能量数值
model = models.Model(ebm_input, ebm_output)
利用 Langevin Dynamics采样
给定一个输出,能量函数只输出一个分数 — 我们如何才能利用该函数来生成一个低能量分的新样本?
我们将使用一种称为 Langevin dynamics 的新技术, 该技术利用了一个事实: 我们可以计算能量函数相对于输入的梯度。如果我们从采样空间一个随机点出发,每次沿着计算梯度的反方向走一小步,我们将逐渐减少能量函数。如果我们的网络训练得当,那么随机噪声将会逐渐转化为一幅人眼看起来像是从原来训练集分布抽取的观察。
| 统计梯度Langevin Dynamics |
|---|
| 重要的是,当我们在样本空间遍历时,我们必须加少量随机噪声到输入中。否则的话,就有陷入局部最小值的风险。这项技术因此得名 “统计梯度 Langevin dynamics”。 |
对于一个二维空间,能量函数值在第三维的情况,我们可以将梯度下降进行可视化,如下图7-4所示。路径是一个噪声的下山路径,遵从能量函数 E ( x ) E(x) E(x) 相对于输入x的负梯度。在 MNIST 数据集中,我们有1024个像素,因此需要探索 1024维空间,但基本的准则是一样的。

值得注意的是,这种梯度下降和通常用于训练神经网络的梯度下降是有区别的。当训练神经网络时,我们通过反向传播计算损失函数相对于网络参数(也即,权重)的梯度 。然后沿着反梯度方向对参数进行小幅度更新,从而使得在大多数迭代轮次,损失逐渐最小化。
对Langevin Dynamics来说,我们保持网络权重不变,计算输出相对于输入的梯度。然后我们在负梯度方向上对输入进行小幅度更新,从而使得在大多数迭代轮次,输出(也就是能量分数)逐渐最小化。
两个过程都利用了同样的思想 (梯度下降),但是应用于不同的函数和不同实体。
正式来说,Langevin dynamics可以用下面的方程描述:
x k = x k − 1 − η ∇ x E θ ( x k − 1 ) + ω x^k = x^{k-1} - \eta \nabla_x E_\theta(x^{k-1})+\omega xk=xk−1−η∇xEθ(xk−1)+ω
其中, ω ∼ N ( 0 , σ ) \omega \sim \mathcal{N}(0,\sigma) ω∼N(0,σ), x 0 ∼ U ( − 1 , 1 ) x^0 \sim \mathcal{U}(-1,1) x0∼U(−1,1)。 η \eta η 是需要调优的步长超参数 — 太大的话会跳过极小值,太小的话算法会收敛过慢。
| 小贴士 |
|---|
| x 0 ∼ U ( − 1 , 1 ) x^0 \sim \mathcal{U}(-1,1) x0∼U(−1,1)是 [ − 1 , 1 ] [-1,1] [−1,1]范围内的均匀分布。 |
样例7-4给出了我们代码实现的 Langevin 采样函数。
# Langevin 采样函数
def generate_samples(model, inp_imgs, steps, step_size, noise):
imgs_per_step = []
# 针对给定的steps数进行循环
for _ in range(steps):
# 在图像上增加少量噪声
inp_imgs += tf.random.normal(inp_imgs.shape, mean = 0, stddev = noise)
inp_imgs = tf.clip_by_value(inp_imgs, -1.0, -1.0)
with tf.GradientTape() as tape:
tape.watch(inp_imgs)
# 将图像传入模型得到能量分数
out_score = -model(inp_imgs)
grads = tape.gradient(out_score, inp_imgs)
grads += tf.clip_by_value(grads, -0.03, 0.03)
# 在输入图像上加上少量的梯度
inp_imgs += -step_size * grads
inp_imgs = tf.clip_by_value(inp_imgs, -1.0, -1.0)
return inp_imgs
使用Contrastive Divergence进行训练
既然我们已经知道如何从样本空间采样一个新的低能量点,让我们将关注力转向模型训练。
我们没法直接使用最大似然估计,因为能量函数不能输出一个概率,它输出的是一个在样本空间上积分不为1的分数。我们将使用Geoffrey Hinton在2002年提出的一项名为 contrastive divergence的技术来训练未归一化分数的模型。
我们想要最小化的值是数据的负对数似然:
L = − E x ∼ d a t a [ l o g p θ ( x ) ] \mathcal{L} = - \mathbb{E}_{x \sim data}[log p_\theta(\mathbf{x})] L=−Ex∼data[logpθ(x)]
当 p θ ( x ) p_\theta(\mathbf{x}) pθ(x)是玻尔兹曼分布 且能量函数为 E θ ( x ) E_\theta(\mathbf{x}) Eθ(x)时, 可以证明其梯度可以写作以下形式(完整推导参见 Oliver Woodford 的 Notes on Contrastive Divergence):
∇ θ L = E x ∼ d a t a [ ∇ θ E θ ( x ) ] − E x ∼ m o d e l [ ∇ θ E θ ( x ) ] \nabla_\theta\mathcal{L} = \mathbb{E}_{x \sim data}[\nabla_\theta E_\theta(\mathbf{x})]-\mathbb{E}_{x \sim model}[\nabla_\theta E_\theta(\mathbf{x})] ∇θL=Ex∼data[∇θEθ(x)]−Ex∼model[∇θEθ(x)]
直观上,上式是有意义的 — 我们想要训练模型以对真实观察输出较大的负能量分数,对生成的假观察输出大的正能量分数,从而使得,这两个极端的对比度越大越好。
换句话说,我们可以计算真、假样本间的能量分数差异,并用它作为我们的损失函数。
为了计算假样本的能量分数,我们需要能够从分布 p θ ( x ) p_\theta(\mathbf{x}) pθ(x)进行采样,而由于不易于处理的分母这是不可能的。因此,我们使用 Langevin 采样方法来生成一组能量分数较低的观察。这一过程可能需要运行无数多步来生成一个完美的样本(显然这是不实际的),因此,我们运行少量的步数,假设这也能足够产生有意义的损失函数。
我们也维护了之前迭代的一些样本缓存,使得我们用它们作为下一个batch的起点,而无需从纯噪声开始。用以生成采样buffer的代码如下样例 7-5所示。
class Buffer:
def __init__(self, model):
super().__init__()
# 采样buffer初始化为一组随机噪声
self.model = model[
tf.random.uniform(shape = (1,32,32,1)) * 2 - 1
for _ in range(128)
]
def sample_new_exmps(self, steps, step_size, noise):
# 平均来讲,每次5%的观察是从零开始(也即,随机噪声)生成的
n_new = np.random.binomial(128, 0.05)
rand_imgs = (tf.random.uniform((n_new, 32, 32, 1)) * 2 - 1)
# 其余的直接从已有的缓存中随机抽取
old_imgs = tf.concat(random.choices(self.examples, k = 128 - n_new), axis = 0)
# 新老样本连接起来并通过Langevin取样器
inp_imgs = tf.concat([rand_imgs, old_imgs], axis=0)
inp_imgs = generate_samples(self.model, inp_imgs, steps=steps, step_size=step_size, noise=noise)
# 结果样本加入buffer,修剪到最长为8192个观察
self.examples = tf.split(inp_imgs, 128, axis = 0) + self.examples
self.examples = self.examples[:8192]
return inp_imgs
图7-5展示了一个训练步骤的contrastive divergence。算法会把真实观察的分数推下来,把虚假观察的分数拉上去,而不关心在每步之后如何归一化分数。
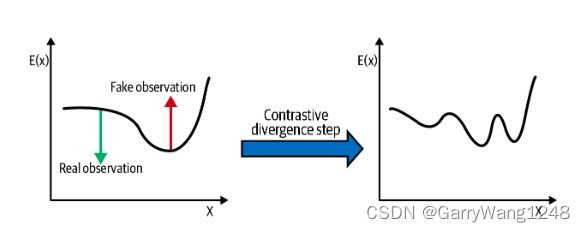
我们可以利用Keras Model对 contrastive divergence算法的训练步骤进行编码,如下样例7-6所示。
# 使用contrastive divergence 进行 EBM训练
class EBM(models.Model):
def __init__(self):
super(EBM,self).__init__()
self.model = model
self.buffer = Buffer(self.model)
self.alpha = 0.1
self.loss_metric = metrics.Mean(name="loss")
self.reg_loss_metric = metrics.Mean(name="reg")
self.cdiv_loss_metric = metrics.Mean(name="cdiv")
self.real_out_metric = metrics.Mean(name="real")
self.fake_out_metric = metrics.Mean(name="fake")
@property
def metrics(self):
return [
self.loss_metric,
self.reg_loss_metric,
self.cdiv_loss_metric,
self.real_out_metric,
self.fake_out_metric
]
def train_step(self, real_imgs):
# 在真实图像上叠加少量噪声,以避免模型过拟合到训练集
real_imgs += tf.random.normal(
shape=tf.shape(real_imgs), mean=0, stddev=NOISE
)
real_imgs = tf.clip_by_value(real_imgs, -1.0, 1.0)
# 从buffer中采样一组假图
fake_imgs = self.buffer.sample_new_exmps(
steps=STEPS, step_size=STEP_SIZE, noise=NOISE
)
inp_imgs = tf.concat([real_imgs, fake_imgs], axis=0)
with tf.GradientTape() as training_tape:
# 真实图像和虚假图像都通过模型以生成真实和虚假分数
real_out, fake_out = tf.split(self.model(inp_imgs), 2, axis=0)
# CD 损失就是真实观察和虚假观察的分数之差
cdiv_loss = tf.reduce_mean(fake_out, axis=0) - tf.reduce_mean(
real_out, axis=0
)
# 还需要加上对于网络权重的正则损失
reg_loss = self.alpha * tf.reduce_mean(
real_out**2 + fake_out**2, axis=0
)
loss = cdiv_loss + reg_loss
#
grads = training_tape.gradient(loss, self.model.trainable_variables)
self.optimizer.apply_gradients(
zip(grads, self.model.trainable_variables)
)
self.loss_metric.update_state(loss)
self.reg_loss_metric.update_state(reg_loss)
self.cdiv_loss_metric.update_state(cdiv_loss)
self.real_out_metric.update_state(tf.reduce_mean(real_out, axis=0))
self.fake_out_metric.update_state(tf.reduce_mean(fake_out, axis=0))
return {m.name: m.result() for m in self.metrics}
# 当validation时使用,计算 一组随机噪声 和 训练集数据之间的CD损失。可以度量模型训练的程度 (参见下面的章节)
def test_step(self, real_imgs):
batch_size = real_imgs.shape[0]
fake_imgs = (
tf.random.uniform((batch_size, IMAGE_SIZE, IMAGE_SIZE, CHANNELS))
* 2
- 1
)
inp_imgs = tf.concat([real_imgs, fake_imgs], axis=0)
real_out, fake_out = tf.split(self.model(inp_imgs), 2, axis=0)
cdiv = tf.reduce_mean(fake_out, axis=0) - tf.reduce_mean(
real_out, axis=0
)
self.cdiv_loss_metric.update_state(cdiv)
self.real_out_metric.update_state(tf.reduce_mean(real_out, axis=0))
self.fake_out_metric.update_state(tf.reduce_mean(fake_out, axis=0))
return {m.name: m.result() for m in self.metrics[2:]}
EBM分析
训练过程的曲线和支撑度量如下图7-6所示。

首先,注意到训练过程中的损失近似常量,在不同的epochs间变化很小。在模型一直改进的同时,用以和训练集中真实图像进行对比的buffer中生成图像的质量也一直在改进,所以我们可以预期训练损失不会显著下降。
因此,要评估模型性能,我们也设置了一个验证过程,该过程不从buffer中采样,而是对一个随机噪声采样进行评分,并把该评分和训练集样本分数进行比较。如果模型在持续改进,我们将看到 CD 随着 epochs 迭代下降 (也即,它越来越擅长于将真实图像与随机噪声进行区分),如图7-6所示。
从EBM生成新的样本就是从某个支点出发(随机噪声),简单的对一些训练步运行 Langevin 采样器,如图7-7所示。遵从打分函数对于输入的梯度,观察被强制下山(downhill),因此一个可靠的观察可以从噪声之外产出。
# 利用EBM生成新的观察
start_imgs = np.random.uniform(size = (10, 32, 32, 1)) * 2 - 1
gen_img = generate_samples(
ebm.model,
start_imgs,
steps=1000,
step_size=10,
noise = 0.005,
return_img_per_step=True,
)
经过50轮训练之后,采样器的一些观察样例如下图7-7所示。

我们甚至可以展示一个单一的观察是如何在Langevin采样过程中一步步生成的,如下图7-8所示。

其他的EBM
在前面的例子中,我们使用contrastive divergence 及 Langevin dynamics采样器训练了一个深度EBM。但是,早期的EBM模型并没有使用Langevin采样,而是依赖于其他的技术和架构。
早期的一个EBM是玻尔兹曼机。这是一个全连接,无方向的神经网络,其中二值单元室 可见 (v) 或者 隐藏的(h)。一个给定配置神经网络的能量定义如下:
E θ ( v , h ) = 1 2 ( v T L v + h T J h + v T W h ) E_\theta(v,h) = \frac{1}{2}(v^TLv + h^TJh + v^TWh) Eθ(v,h)=21(vTLv+hTJh+vTWh)
其中 W , L , J W, L, J W,L,J 是模型学得的权重矩阵。训练是通过contrastive divergence得到的,但是用的是吉布斯采样来在可见和隐藏层轮询,直到取得一个平衡。在实操中,这个过程很慢,并且无法规模化推广到大量的隐层单元。
| 小贴士 |
|---|
| 关于吉布斯采样的一个绝佳例子,请参考Jessica stringham的博客 “Gibbs Sampling in Python” |
这个模型的一个拓展,所谓的受限玻尔兹曼机(restricted Boltzmann machine, RBM) 移除了相同类型单元间的连接,因而构建了一个两层的,由两部分组成的图。这使得 RBMs 可以堆叠形成深度信念网络 (deep belief networks) ,以对更复杂的分布进行建模。但是,使用RBMs建模高维数据目前仍然不现实,因为吉布斯采样耗时甚费。
直到2000年后,EBMs才开始展现其对更高维数据集的建模潜力,一个构建深度 EBMs的框架才开始建立。 Langevin dynamics 开始在 EBMs采样方法中变得受欢迎,其随后演化为一个名为 score matching 的训练技术。这进一步发展成一类名为 Denoising Diffusion Models的方法,该方法目前是生成式模型的统治方法,应用在 DALL.E2 和 ImageGen等系统重。我们将在第八章进一步探讨扩散模型的更多细节。
本章小结
基于能量的方法是一类生成式模型,它利用了能量评分函数 — 一个对真实观察输出较低分数,对虚假观察输出较高分数的神经网络。给定这个打分函数,计算其概率分布要求归一化一个复杂的分母。EBMs通过两个技巧规避了这一问题: 用以进行网络训练的contrastive divergence ,以及用以进行新观察采样的 Langevin dynamics。
能量函数的训练是通过最小化生成样本分数和训练样本分数之差来实现,这个技术被称为 contrastive divergence。该技术可被证明与最小化负的对数似然等价,这正是最大似然估计所要求的。同时可以规避不易计算的归一化分母。实践中,我们对虚假样本的采样过程进行近似,以确保算法的高效。
深度EBMs的采样是已通过Langevin采样来实现,该技术使用能量分数相对于输入图像的梯度对输入进行小步更新(遵从梯度下降的方向)来逐渐将随机噪声转换为合理的观察。这相对于早期方法(如受限玻尔兹曼机RBM)的吉布斯采样有了显著提升。
