生成式深度学习(第二版)-译文-第八章-扩散模型(I)

终于到了扩散模型，开心！

章节目标

• 了解定义一个扩散模型的底层原则和要素。
• 清楚前向过程是如何给训练图像集添加噪声的。
• 理解重参数化技巧以及为何该技巧是重要的。
• 探索前向扩散的不同形式。
• 理解逆向扩散过程，以及它是如何和前向加噪过程关联的。
• 探索 U-Net架构，该架构用于逆向扩散过程的参数化。
• 使用Keras来构建你自己的去噪扩散模型 (denoising diffusion model, DDM) 以生成鲜花图像。
• 从你的模型中采样新的鲜花图像。
• 探索扩散步数对图像质量的影响，以及如何在隐空间对两幅图像进行插值。

与 GANs一样，扩散模型(diffusion models)也是过去十年提出的，用于图像生成的最具影响力的生成式建模技术之一。在很多benchmarks中，扩散模型已经超过了之前的经典GANs模型，已经迅速成为生成式建模从业者 (尤其是视觉领域的文生图应用，如OpenAI的DALL.E 2和谷歌的Imagen) 之首选。最近，扩散模型开始爆炸式应用于一系列的任务，让人想起2017到2020年GAN的繁荣。

其实，扩散模型背后的很多核心思想与本书之前介绍的几种生成式模型 (例如，去噪自编码器，基于能量的模型) 有不少共同点。实际上，其名字中的扩散 (diffusion) 灵感来自于热力学扩散中广为研究的性质: 2015年在纯物理领域和深度学习领域构建了一个重要的连接。

在基于分数的生成式模型领域 (基于能量模型的一个分支，为了训练模型，它会直接估计对数分布【也称为分数函数】的梯度，而不是使用contrastive divergence) 也取得了重要进展。尤其的， Yang Song 及 Stefano Ermon 将多尺度噪声扰动加到裸数据上，以确保模型(一个噪声条件分数网络，a noise conditional score network)在低数据密度区域亦能表现良好。

扩散模型的突破性论文发表于2020年夏天。该论文站在早期工作的肩膀上，揭示了扩散模型和基于分数的生成式模型的一个深度连接，并且用这个连接关系来训练了一个可在多个数据库上与GANs广泛竞争的扩散模型，该模型被称为 去噪扩散概率模型 (Denoising Diffusion Probabilistic Model, DDPM)。

本章将探访那些有助于理解扩散模型工作机制的理论要求。你也将学会如何利用 Keras 构建自己的去噪扩散模型。

引言

为了帮助你理解扩散模型背后的核心思想，让我们从一则短故事开始。

扩散电视 (DiffuseTV)
你站在一家售卖电视机的电子商店里。但是，这个商店显然不同于过往你看到的那些。这里没有各种各样的品牌，只有几百台同样的电视序列相连，一直延伸到商店的后部。另外，前面的几台电视看起来除了一些随机的静态噪声之外啥都没有 (图8-1)。
店主走上前来，询问你是否需要帮助。你好奇的询问她商店的古怪配置。她一边沿着电视的排布向商店深处走去，一边跟你解释这是将要颠覆娱乐产业的新型扩散电视，以及它的工作机制。
她解释到: 在生成过程中，我们给扩散电视看了数以千计其他电视放映的图片 — 但是每个图片都被随机静态噪声逐渐腐蚀，直到和纯噪声之间完全不可区分。这些扩散电视则被设计为小步去除随机噪声，直到最终成果预测噪声添加之前原始图片的样子。你将发现，随着你进一步深入商店，每个电视上的图像实际上都比前面逐渐清晰。
最终，你到了电视的最后一排，这里你能看到完美的图像。这显示是一项聪明的技术，你很好奇这对于观众有多大用处。店主继续她的解释。
对观众来说，他不再是选择一个频道来观看，而是选择一个随机的初始配置。每个配置都将导致完全不同的输出图像，在一些模型中，输出甚至可以通过你输入的文本提示词 (text prompt) 来进行引导。正常的电视机通常只有有限的频道可供观看，而扩散电视则给了观众无限的选择和自由来在屏幕上生成他想看的任何东西。
你马上买了一台扩散电视，同时也放心的听到商店里的长排电视仅仅只是为了展示目的，你不需要同步买下一座仓库来存放你的新设备。

扩散电视的故事描述了扩散模型背后的一般思想。现在，让我们深入技术细节，来看看我们如何利用Keras来构建这样一个模型。

去噪扩散模型 (Denoising Diffusion Models, DDM)

去噪扩撒模型背后的核心思想比较简单 — 我们可以训练一个深度学习模型来使用一系列的小步骤对图像进行去噪。如果我们从纯噪声出发，理论上我们可以一直使用模型，直到我们最终得到一幅看起来像是从训练集中抽取的图像。令人吃惊的地方在于，这个简单的概念在实操中居然是可行的！

让我们首先准备好一个数据集，然后一起探索 前向 (加噪) 和 后向 (去噪) 扩散过程。

运行本例代码
本例代码可以通过Jupyter Notebook在随书附带代码库的以下路径找到: notebooks/08_diffusion/01_ddm/ddm.ipynb。该代码是从 Keras 官网上由 Andras Beres 等贡献的 tutorial on denoising diffusion implicit models 上创建。

鲜花数据集

我们将使用Kaggle上可公开获取的 Oxford 102 Flower dataset。该数据集由各种花朵的8000幅彩色图像组成。

如下样例8-1所示，你可以使用本书代码库中的Kaggle dataset downloader脚本来下载数据集。鲜花图片会存放在/data 文件夹。

bash scripts/download_kaggle_data.sh nunenuh pytorch-challenge-flower-dataset

同以往一样，我们将使用 Keras 的 image_dataset_from_directory 函数来加载图像，并将图像 resize 到 64 x 64 像素，像素值放缩到 [0,1] 范围。我们也将该数据集重复五遍以增加 epoch 长度，并将数据按 64张图像一组进行批量化处理，如下样例8-2所示。

# 加载 Oxford 102 Flower dataset

# 使用 Keras image_dataset_from_directory 函数加载数据集 (训练需要时)
train_data = utils.image_dataset_from_directory(
    "/app/data/pytorch-challange-flower-dataset/dataset",
    labels=None,
    image_size=(64, 64),
    batch_size=None,
    shuffle=True,
    seed=42,
    interpolation="bilinear",
)

# 将像素值放缩到 [0,1] 范围
def preprocess(img):
    img = tf.cast(img, "float32") / 255.0
    return img

train = train_data.map(lambda x: preprocess(x))
# 数据集重复五次
train = train.repeat(5)
# 数据集按照64张图像进行批次聚合
train = train.batch(64, drop_remainder=True)

数据集的样例图像如下图 8-2 所示。

既然现在有了数据集，我们现在可以探索如何使用前向扩散过程给图像添加噪声。

前向扩散过程

假定我们有一个图像 ${\mathbf{x}}_0$, 并且我们希望通过一系列步骤 (例如，$T=1000$) 来逐渐对图像进行腐蚀，使得最终的腐蚀结果看起来与标准高斯噪声无差别（也即，${\mathbf{x}}_T$应该是 0 均值，单位方差）。我们该如何做到这一点呢？

我们可以定义一个函数 $q$ ，它可以给一幅图像 ${\mathbf{x}}_{t-1}$添加少量方差为${\beta }_t$的高斯噪声来生成一幅新的图像 ${\mathbf{x}}_t$。如果我们一直使用该函数，我们将生成一系列渐进式噪声图像$({\mathbf{x}}_0,\cdots ,{\mathbf{x}}_T)$, 如下图8-3所示。

数学上，我们可以将这一更新过程以下面的方程表示 (这里，${ϵ}_{t-1}$是0均值单位方差的标准高斯):
${\mathbf{x}}_t=\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1}+\sqrt{{\beta }_t}{ϵ}_{t-1}$

注意，我们也可以对输入图像 ${\mathbf{x}}_{t-1}$进行放缩，以确保输出图像${\mathbf{x}}_t$的方差随着时间变化一直保持为常数。通过这种方式，如果我们将原始图像 ${\mathbf{x}}_0$归一化到0均值单位方差，那么通过下面的推导我们将看到，对于足够大的$T$来说, ${\mathbf{x}}_T$将近似为标准正态分布。

如果我们假设 ${\mathbf{x}}_{t-1}$ 有0均值单位方差，那么利用规则 $Var(aX)=a^{2}Var(X)$，$\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1}$ 将有方差 $1-{\beta }_t$, $\sqrt{{\beta }_t}{ϵ}_{t-1}$ 将有方差 ${\beta }_t$。对于独立变量 X 和 Y，我们利用规则 $Var(X+Y)=Var(X)+Var(Y)$，把上述两者加到一起，我们将得到一个新的分布${\mathbf{x}}_t$，其均值为 0，方差为$1-{\beta }_t+{\beta }_t=1$。因此，如果我们把${\mathbf{x}}_0$归一化到0均值单位方差，那么我们能确保对所有的${\mathbf{x}}_t$ (包括最终的图像 ${\mathbf{x}}_T$) 都成立, 它们都近似是一个标准高斯分布。这正是我们想要的，因为我们想要从 ${\mathbf{x}}_T$中轻松取样，并在我们训练的神经网络模型中运行逆的扩散过程！

换句话说，我们的前向加噪过程 $q$ 可以写作如下形式:
$q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})=\mathcal{N}({\mathbf{x}}_t;\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I})$

重参数化技巧 (Reparameterization Trick)

如果我们可以从一幅图像${\mathbf{x}}_0$直接跳转到任何加噪版本${\mathbf{x}}_t$, 而无需使用 $t$ 次 $q$ 函数，这将是大有用处的。幸运的是，我们可以利用一个重参数化技巧来实现这点。

如果我们定义 ${\alpha }_t=1-{\beta }_t$, 并且 ${\bar{a}}_t=\prod _{i=1}^t{a}_i$，那么我们可以写作如下形式:
$$\begin{array}{rl}{\mathbf{x}}_t& =\sqrt{a_t}{\mathbf{x}}_{t-1}+\sqrt{1-a_t}{ϵ}_{t-1}\\ & =\sqrt{a_t{a}_{t-1}}{\mathbf{x}}_{t-2}+\sqrt{1-a_t{a}_{t-1}}ϵ\\ & =\cdots \\ & =\sqrt{{\bar{a}}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{a}}_t}ϵ\end{array}$$

注意第二行使用了一个事实: 我们可以把两个高斯相加得到一个新的高斯。因此，我们得到了一种方法，可以直接从原始图像${\mathbf{x}}_0$ 出发直接跳转到任何的前向过程 ${\mathbf{x}}_t$。另外，我们可以使用${\bar{a}}_t$值来定义扩散计划 (diffusion schedule)，而无须再用原始的 ${\beta }_t$值，这里的一个解释是: ${\bar{a}}_t$ 是由于信号(原始图像 \mathbf{x}_0) 产生的方差，$1-{\bar{a}}_t$ 是由于噪声($ϵ$) 产生的方差。

因此，前向扩散过程$q$可以写作如下形式:
$q({\mathbf{x}}_t|{\mathbf{x}}_0)=\mathcal{N}({\mathbf{x}}_t;\sqrt{a_t}{\mathbf{x}}_0,(1-a_t)\mathbf{I})$

扩散计划 (Diffusion Schedules)

注意，我们也可以在每个时间步 自由选择一个不同的 ${\beta }_t$ — 它们不见得一定要一样。${\beta }_t$ (或者 $a_t$) 值随着时间 $t$ 变化的过程称为扩散计划 (diffusion schedule)。

在Ho等人2020年原始的论文中，作者为 ${\beta }_t$ 选择了一个线性扩散计划 (linear diffusion schedule) — 也即，${\beta }_t$ 随着时间 t 线性增长，从 ${\beta }_1=0.0001$ 到 ${\beta }_T=0.02$。这确保了在早期的加噪过程中，我们采用了相对后期阶段(此时，图像已经有比较大的噪声了)较小的加噪步骤。

样例8-3中，我们编程实现了一个线性扩散计划。

# 样例8-3 线性扩散计划
def linear_diffusion_schedule(diffusion_times):
	min_rate = 0.0001
	max_rate = 0.02
	betas = min_rate + tf.convert_to_tensor(diffusion_times) * (max_rate - min_rate)
	alphas = 1 - betas
	alpha_bars = tf.math.cumprod(alphas)
	signal_rates = alpha_bars
	noise_rates = 1 - alpha_bars
	return noise_rates, signal_rates

T = 1000
# diffusion times 在 0 到 1之间均匀分布
diffusion_times = [x/T for x in range(T)]
# 线性扩散计划应用于duffusion_times 来产生 noise 及 signal rates
linear_noise_rates, linear_signal_rates = linear_diffusion_schedule(diffusion_times)

在一篇稍晚的论文中，研究者发现，余弦扩散计划 (cosine diffusion schedule) 优于原论文提出的线性计划。余弦扩散计划按如下形式定义了${\bar{a}}_t$:
${\bar{a}}_t=co{s}^2(\frac{t}{T}\cdot \frac{\pi }{2})$

因此，更新方差具有如下形式 (使用三角等式 $co{s}^2(x)+si{n}^2(x)=1$):
${\mathbf{x}}_t=cos(\frac{t}{T}\cdot \frac{\pi }{2}){\mathbf{x}}_0+sin(\frac{t}{T}\cdot \frac{\pi }{2})ϵ$

上述方程式论文中使用的实际余弦扩散计划的一个简化版本。作者另外添加了一个偏置项，并且使用放缩来防止在扩散过程之处加噪steps过小。如样例8-4所示，我们可以用代码实现 cosine 和 offset cosine 扩散计划。

# 样例8-4：cosine 及 offset cosine 扩散计划
# 纯 cosine 扩散计划 (无offset 和 rescaling)
def cosine_diffusion_schedule(diffusion_times): 
    signal_rates = tf.cos(diffusion_times * math.pi / 2)
    noise_rates = tf.sin(diffusion_times * math.pi / 2)
    return noise_rates, signal_rates
    
# 我们将使用的offset cosine扩散计划，其调整计划来确保加噪steps在加噪的开始阶段不至于过小。
def offset_cosine_diffusion_schedule(diffusion_times): 
    min_signal_rate = 0.02
    max_signal_rate = 0.95
    start_angle = tf.acos(max_signal_rate)
    end_angle = tf.acos(min_signal_rate)

    diffusion_angles = start_angle + diffusion_times * (end_angle - start_angle)

    signal_rates = tf.cos(diffusion_angles)
	noise_rates = tf.sin(diffusion_angles)

    return noise_rates, signal_rates

对于每个时间 t，我们可以 ${\bar{a}}_t$ 值来查看在 (linear、cosine及offset cosine扩散计划) 过程的每个阶段中，到底有多少信号(${\bar{a}}_t$)和噪声($1-{\bar{a}}_t$)得以通过。结果如下图8-4所示。

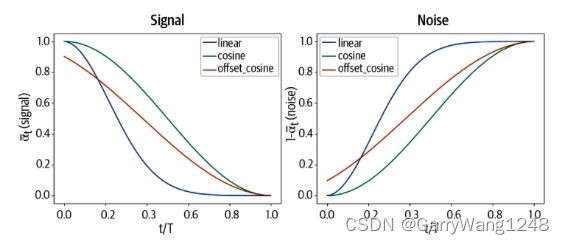
注意在cosine 扩散计划中，噪声的水平攀升的更为缓慢。一个余弦扩散计划相对于线性扩散计划，在噪声添加上更为平缓，因而可以提升训练效率和生成质量。这一点亦可从线性和余弦计划腐蚀的图像中看到，如图8-5所示。

后续部分参考下一篇博文