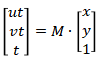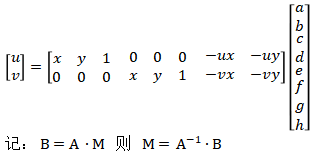【跟官网学opencv-python】笔记3.2:opencv几何变换
目录
前言
目标
函数详解
1.缩放变换
2.平移变换
3.旋转变换
4.仿射变换
5.透视变换
总结
进阶
1、透视变换公式推导
2、透视变换实例应用
参考
前言
跟着官网学习opencv-python才是基础入门的最佳选择,下文是官网的学习记录及扩展!
目标
学习对图像应用不同的几何变换,如平移、旋转、仿射变换等。
涉及函数:cv2.getPerspectiveTransform,cv2.warpAffine和cv2.warpPersperctive
函数详解
OpenCV提供了两个转换函数,cv.warpAffine和cv.warpPerspective,可以用它们执行各种转换。
cv.warpAffine 采用 2x3 变换矩阵作为输入;
cv.warpPerspective 采用 3x3 变换矩阵作为输入。
1.缩放变换
缩放只是调整图像的大小。OpenCV为此附带了一个函数 cv.resize() 。
可以手动指定图像的大小,也可以指定比例因子。
可以使用不同的插值方法。
要缩小图像,通常使用INTER_AREA插值看起来最好;
而放大图像,通常是INTER_CUBIC(慢)或INTER_LINEAR(更快效果一般)一起看起来最好。
默认情况下,插值方法cv.INTER_LINEAR用于调整大小。
函数介绍:
cv2.resize(src, dsize, dst=None, fx=None, fy=None, interpolation=None)
src 输入图像.
dst 输出图像;
dsize 输出图像大小,它的大小为dsize(当它不为零时)或从src.size(),fx和fy计算的大小;
DST 的类型与 SRC 相同.如果它等于零(在 Python 中),则计算为None:
dsize = Size(round(fx*src.cols), round(fy*src.rows))
dsize 或 fx 和 fy 都必须不为零.
fx 沿横轴的比例因子;当它等于 0 时,它的计算为(double)dsize.width/src.cols
fy 沿纵轴的比例因子;当它等于 0 时,它的计算为(double)dsize.height/src.rows显式指定 dsize=dst.size();FX和FY将从中计算出来。
resize(src, dst, dst.size(), 0, 0, interpolation);
如果要在每个方向上以 2 倍抽取图像,可以这样调用函数:
指定 fx 和 fy,并让函数计算目标图像大小。
resize(src, dst, Size(), 0.5, 0.5, interpolation);插值算法:
INTER_NEAREST 最近邻插值
INTER_LINEAR 双线性插值
INTER_CUBIC 双三次插值
INTER_AREA 使用像素面积关系进行重采样。它可能是图像抽取的首选方法,因为它可以提供无摩尔纹的结果。但是当图像缩放时,它类似于INTER_NEAREST方法。.
INTER_LANCZOS4 8x8邻域上的兰索斯插值
INTER_LINEAR_EXACT 位精确双线性插值
INTER_NEAREST_EXACT 位精确最近邻插值。这将产生与PIL,scikit-image或Matlab中的最近邻方法相同的结果.
INTER_MAX 插值码的掩码代码演示:
import cv2 as cv
img = cv.imread('../Resources/moon.jpg')
# 下面的None本应该是输出图像的尺寸,但是因为后面我们设置了缩放因子,所以,这里为None
res = cv.resize(img,None,fx=2, fy=2, interpolation = cv.INTER_CUBIC)
cv.imshow('image1',res)
# OR 这里直接设置输出图像的尺寸,所以不用设置缩放因子
height, width = img.shape[:2]
res = cv.resize(img,(int(0.3*width), int(0.3*height)), interpolation = cv.INTER_AREA)
cv.imshow('image2',res)
cv.waitKey(0)
cv.destroyAllWindows()2.平移变换
平移是对象位置的移动。如果您知道 (x,y) 方向的偏移量(tx,ty),可以创建转换矩阵M如下:
需要把它变成一个类型为 np.float32 的 Numpy 数组,并传递给 cv.warpAffine()函数。
M = np.float32([[1,0,tx],[0,1,ty]])
cv.warpAffine(src, M, dsize, dst=None, flags=None, borderMode=None, borderValue=None)
src 输入图像.
dst 输出图像的大小为 dsize 且类型与 SRC 相同 .
M 2×3的转换矩阵.
dsize **输出图像的大小=(图像的宽,图像的高)=(图像的列数,图像的行数)**.
flags 插值方法(参见插值标志)和可选标志的组合WARP_INVERSE_MAP这意味着 M 是逆变换 ( dst→src ).
borderMode 像素外推法(请参阅边界类型);当borderMode=BORDER_TRANSPARENT时,表示目标图像中与源图像中的“异常值”对应的像素不会被函数修改.
borderValue 在恒定边框的情况下使用的值;默认情况下,它是 0.平移变换公式:
将平移变换应用于图像:函数 warpAffine 使用指定的矩阵转换源图像的计算公式如下:
![]()
dst(x,y)=src(M11x+M12y+M13, M21x+M22y+M23)
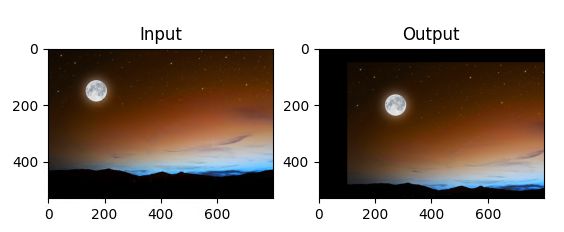
代码演示图像平移(100,50)后的效果:
import numpy as np
import cv2 as cv
img = cv.imread('../Resources/moon.jpg')
rows,cols,_ = img.shape
M = np.float32([[1,0,100],[0,1,50]])
# dst(x,y)=src(1x+0y+100, 0x+1y+50)=src(x+100,y+50)
dst = cv.warpAffine(img,M,(cols,rows))
cv.imshow('img',dst)
cv.waitKey(0)
cv.destroyAllWindows()更改转换矩阵M,还可以实现各种变换操作
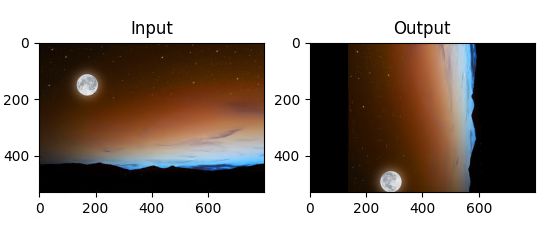
当 M = np.float32([[-1,0,cols],[0,-1,rows]])
可以实现图像XY方向的翻转。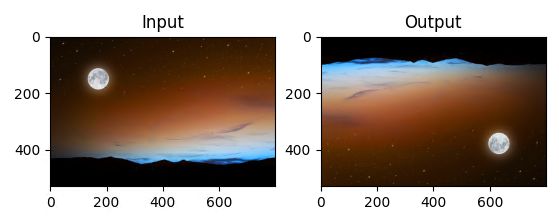
3.旋转变换
对一个图像旋转角度θ,需要使用下面的旋转矩阵:
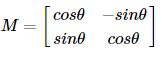
M = np.float32([[cos θ, -sin θ],[sin θ, cos θ]])
但OpenCV允许在任意地方进行旋转,所以旋转矩阵应该为
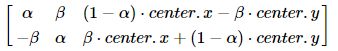
即,M = np.float32([[α, β, (1-α).center_x - β.center_y],[-β, α, β.center_x + (1-α).center_y]])
其中α = scale · cos θ, β = scale · sin θ
为更方便地构建旋转矩阵,OpenCV提供了一个旋转矩阵构建函数cv2.getRotationMatrix2D。
cv2.getRotationMatrix2D(center, angle, scale)
center 源图像中的旋转中心.
angle 旋转角度(以度为单位)。正值表示逆时针旋转(假定坐标原点为左上角).
scale 各向同性比例因子,即旋转后的缩放因子.可以通过设置旋转中心,缩放因子以及窗口大小来防止旋转后超出边界的问题。
代码演示:
from matplotlib import pyplot as plt
import numpy as np
import cv2 as cv
img = cv.imread('../Resources/moon.jpg')
rows,cols,_ = img.shape
# 旋转矩阵 cols-1 and rows-1 are the coordinate limits.
M = cv.getRotationMatrix2D(((cols-1)/2.0,(rows-1)/2.0),90,1)
dst = cv.warpAffine(img,M,(cols,rows))
plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
plt.show()
cv.imshow('img',dst)
cv.waitKey(0)
cv.destroyAllWindows()
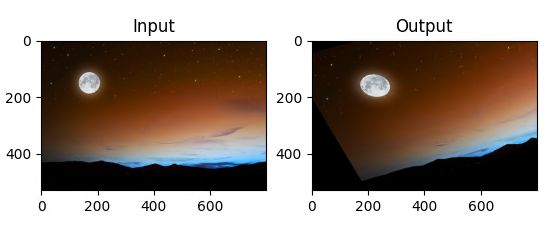
4.仿射变换
在仿射变换中,原图中所有平行线在结果图像中同样平行。
为创建这个矩阵,需要从原图像中找到三个点以及他们在输出图像中的位置,然后cv2.getAffineTransForm()会创建一个2X3的矩阵。
最后这个矩阵会被传给函数cv2.warpAffine()
矩阵构建方法如下:
cv.getAffineTransform(src,dst)
pts1 = np.float32([[50,50],[200,50],[50,200]])
pts2 = np.float32([[10,100],[200,50],[100,250]])
M = cv.getAffineTransform(pts1,pts2)代码演示:
from matplotlib import pyplot as plt
import numpy as np
import cv2 as cv
img = cv.imread('../Resources/moon.jpg')
rows,cols,_ = img.shape
# 仿射变换
pts1 = np.float32([[50,50],[200,50],[50,200]])
pts2 = np.float32([[10,100],[200,50],[100,250]])
M = cv.getAffineTransform(pts1,pts2)
dst = cv.warpAffine(img,M,(cols,rows))
plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
plt.show()
cv.imshow('img',dst)
cv.waitKey(0)
cv.destroyAllWindows()
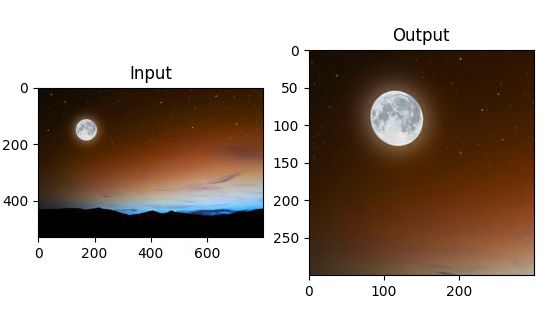
5.透视变换
对于透视变换,我们需要一个3x3转换矩阵。在变换前后直线还是直线。
需要在原图上找到4个点,以及他们在输出图上对应的位置,这四个点中任意三个都不能共线,
可以通过函数cv2.getPerspectiveTransform()构建,然后这个矩阵传给函数v2.warpPerspective()。
矩阵构建方法如下:
cv2.getPerspectiveTransform(src, dst, solveMethod=None)
src 源图像中四边形顶点的坐标.
dst 目标图像中相应四边形顶点的坐标.
solveMethod 传递给 cv::solve 的方法(分解类型)从四对对应点计算透视变换矩阵。
cv2.warpPerspective(src, M, dsize, dst=None, flags=None, borderMode=None, borderValue=None)
src 输入图像.
M 3×3 转换矩阵.
dsize 输出图像的大小.
dst 输出图像的大小为 dsize 且类型与 SRC 相同 .
flags 插值方法(INTER_LINEAR 或 INTER_NEAREST)和可选标志WARP_INVERSE_MAP的组合,将 M 设置为逆变换 (DST→SRC).
borderMode 像素外推法(BORDER_CONSTANT或BORDER_REPLICATE)。
borderValue 在恒定边框的情况下使用的值;默认情况下,它等于 0.透视变换公式:
from matplotlib import pyplot as plt
import numpy as np
import cv2 as cv
img = cv.imread('../Resources/moon.jpg')
rows,cols,_ = img.shape
# 透视变换
pts1 = np.float32([[56,65],[368,52],[28,387],[389,390]])
pts2 = np.float32([[0,0],[300,0],[0,300],[300,300]])
M = cv.getPerspectiveTransform(pts1,pts2)
print(M)
dst = cv.warpPerspective(img,M,(300,300))
plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
plt.show()
cv.imshow('img',dst)
cv.waitKey(0)
cv.destroyAllWindows()
总结
平移、旋转、放射变换都是通过构造2X3的矩阵,然后传入 cv.warpAffine() 来实现的;
透视变换是通过构造3X3的矩阵,然后传入 cv.warpPerspective() 来实现的。
进阶
1、透视变换公式推导
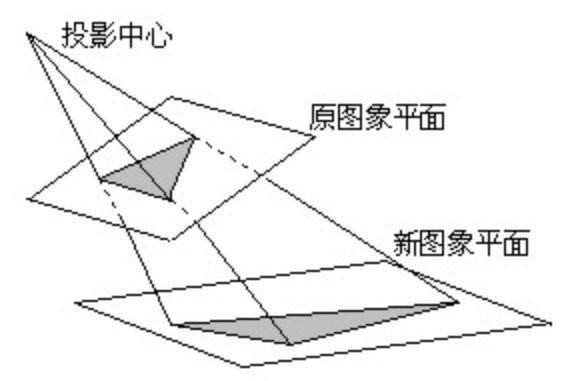
透视变换(Perspective Transformation)是指利用透视中心、像点、目标点三点共线的条件,将一个平面通过一个投影矩阵投影到指定平面上,也称作投影映射(Projective Mapping)。如下图所示:
透视变换公式推导:
上式展开:
ut=ax+by+c
vt=dx+ey+f
t=gx+hy+i
将t带入后整理如下:
iu=ax+by+c-gux-huy
iv=dx+ey+f-gvx-hvy
为便于计算,等式两边约去i,即令i=1,
u=ax+by+c-gux-huy
v=dx+ey+f-gvx-hvy
将上式变换为矩阵形式:
将已知的四对对应的点坐标带入上式即可得到8个参数方程,进而可以求出M矩阵中的8个未知参数。
通过求中间8x8的矩阵的逆矩阵,然后乘上UV矩阵即可得到M矩阵。
2、透视变换实例应用
矫正存在透视畸变的poker图像。
实现思路:
*cv2.Canny算子检测边缘;
*cv2.HoughLinesP霍夫变换获取目标四条直边;
*根据四条边计算四个交点,并按照顺时针排序四个坐标;
*根据四个坐标计算出转换后的目标坐标;
*计算变换矩阵,并利用透视变换算法矫正图像;
import cv2
import numpy as np
# 读取图像
img = cv2.imread("../Resources/poker.png")
# 将原图转为灰度图
gray_img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# Canny边缘检测
canny_img = cv2.Canny(gray_img, 240, 250, 3)
# 显示边缘检测后的图像
cv2.imshow("canny_img", canny_img)
cv2.waitKey(0)
def draw_line(img, lines):
# 绘制直线
for line_points in lines:
cv2.line(img, (line_points[0][0], line_points[0][1]), (line_points[0][2], line_points[0][3]),
(0, 255, 0), 2, 8, 0)
cv2.imshow("line_img", img)
cv2.waitKey(0)
# #Hough直线检测
lines = cv2.HoughLinesP(canny_img, 1, np.pi / 180, 100, minLineLength=30, maxLineGap=10)
# 基于边缘检测的图像来检测直线
draw_line(img, lines)
# 计算四条直线的交点作为顶点坐标
def computer_intersect_point(img,lines):
def get_line_k_b(line_point):
"""计算直线的斜率和截距
:param line_point: 直线的坐标点
:return:
"""
# 获取直线的两点坐标
x1, y1, x2, y2 = line_point[0]
# 计算直线的斜率和截距
k = (y1 - y2) / (x1 - x2)
b = y2 - x2 * (y1 - y2) / (x1 - x2)
return k, b
# 用来存放直线的交点坐标
line_intersect = []
for i in range(len(lines)):
k1, b1 = get_line_k_b(lines[i])
for j in range(i + 1, len(lines)):
k2, b2 = get_line_k_b(lines[j])
# 计算交点坐标
x = (b2 - b1) / (k1 - k2)
y = k1 * (b2 - b1) / (k1 - k2) + b1
if img.shape[1] > x > 0 and img.shape[0] > y > 0:
line_intersect.append((int(np.round(x)), int(np.round(y))))
return line_intersect
def draw_point(img, points):
for position in points:
cv2.circle(img, position, 5, (0, 0, 255), -1)
cv2.imshow("draw_point", img)
cv2.waitKey(0)
# 计算直线的交点坐标
line_intersect = computer_intersect_point(img, lines)
import traceback
try:
assert len(line_intersect)==4
except AssertionError:
print('intersect_point_error: ', "Points count is not 4! Adjust Canny or HoughLinesP param to get 4 right points pls!")
traceback.print_exc()
# 绘制交点坐标的位置
draw_point(img, line_intersect)
def order_point(points):
"""对交点坐标进行排序
:param points:
:return:
"""
points_array = np.array(points)
# 对x的大小进行排序
x_sort = np.argsort(points_array[:, 0])
# 对y的大小进行排序
y_sort = np.argsort(points_array[:, 1])
# 获取上方两点,根据X排序再分开得到lu, ru
up_two=points_array[y_sort[:2]]
up_two_sort = np.argsort(up_two[:, 0])
lu_point=up_two[up_two_sort[0]]
ru_point = up_two[up_two_sort[1]]
# 获取下方两点,根据X排序再分开得到ld, rd
down_two = points_array[y_sort[2:]]
down_two_sort = np.argsort(down_two[:, 0])
ld_point = down_two[down_two_sort[0]]
rd_point = down_two[down_two_sort[1]]
# 输出点坐标应按照顺时针顺序排列
return np.array([lu_point,ru_point,rd_point,ld_point], dtype=np.float32)
def target_vertax_point(clockwise_point):
# 计算顶点的宽度(取最大宽度)
w1 = np.linalg.norm(clockwise_point[0] - clockwise_point[1])
w2 = np.linalg.norm(clockwise_point[2] - clockwise_point[3])
w = w1 if w1 > w2 else w2
# 计算顶点的高度(取最大高度)
h1 = np.linalg.norm(clockwise_point[1] - clockwise_point[2])
h2 = np.linalg.norm(clockwise_point[3] - clockwise_point[0])
h = h1 if h1 > h2 else h2
# 将宽和高转换为整数
w = int(round(w))
h = int(round(h))
# 计算变换后目标的顶点坐标
top_left = [0, 0]
top_right = [w, 0]
bottom_right = [w, h]
bottom_left = [0, h]
return np.array([top_left, top_right, bottom_right, bottom_left], dtype=np.float32)
# 对原始图像的交点坐标进行排序
clockwise_point = order_point(line_intersect)
print(clockwise_point)
# 获取变换后坐标的位置
target_clockwise_point = target_vertax_point(clockwise_point)
print(target_clockwise_point)
# 计算变换矩阵
matrix = cv2.getPerspectiveTransform(clockwise_point, target_clockwise_point)
print(matrix)
# 计算透视变换后的图片
perspective_img = cv2.warpPerspective(img, matrix,
(int(target_clockwise_point[2][0]), int(target_clockwise_point[2][1])))
cv2.imshow("perspective_img", perspective_img)
cv2.waitKey(0)
透视变换效果如下:
参考
OpenCV: OpenCV-Python Tutorials
基于改进Hough变换和透视变换的透视图像矫正_爱学术 (ixueshu.com)
透视变换原理实例代码详解_修炼之路的博客-CSDN博客
学习、进步、坚持。。。内容不间断更新中。。。