(清风)数学建模:模糊分析法(二)应用
模糊综合评价
- 评价问题概述
- 一级模糊综合评价模型
-
- 举例
-
- 某单位对员工的年终综合评定
- 空气质量评定
- 露天煤矿的边坡设计方案
- 多级模糊综合评价模型
-
- 引入多级的原因
- 二级模糊综合评价模型
-
- 操作步骤
- 举例
- 三级模糊综合评价模型
评价问题概述
评价问题是要把论域的对象对应评语集中指定的评语或者将方案作为评语集并选择一个最优方案。
在模糊综合评价中引入了三个集合
- 因素集(评价指标集):U={u1,u2,…un}
- 评语集(评价的结果):V={v1,v2,…vm}
- 权重集(指标的权重):A={a1,a2,…an}
eg:评价一名学生的表现
U={专业排名、课外实践、志愿服务、竞赛成绩}
V={优、良、差}
A={0.5、0.1、0.1、0.3}
一级模糊综合评价模型
步骤
1. 确定因素集:U={u1,u2,…un}
2. 确定评语集:V={v1,v2,…vm}
3. 确定各因素的权重:A={a1,a2,…an}
4. 确定模糊综合判断矩阵:R={ri1,ri2,…rim}
ri1:指标ui对评语1的隶属度
ri2:指标ui对评语2的隶属度
rim:指标ui对评语m的隶属度
各指标模糊综合判断矩阵为:
R = [ r 11 r 12 . . . r 1 m r 21 r 22 . . . r 2 m . . . . . . . . . . . . r n 1 r n 2 . . . r n m ] R= \left[ \begin{matrix} r_{11}& r_{12} & ...& r_{1m} \\ r_{21} & r_{22} & ...& r_{2m} \\ ...& ... & ...&...\\ r_{n1}& r_{n2} & ...& r_{nm} \\ \end{matrix} \right] R=⎣⎢⎢⎡r11r21...rn1r12r22...rn2............r1mr2m...rnm⎦⎥⎥⎤
它是一个从U到V的模糊关系矩阵(第一列表示各个指标对评语1的隶属度)
5. 综合评判
如果有一个从U到V的模糊关系 R = ( r i j ) n × m R=(r_{ij})_{n×m} R=(rij)n×m,那么利用R就可以得到一个模糊变换
T R : F ( U ) → F ( V ) \begin{aligned} T_R:F(U)→F(V) \end{aligned} TR:F(U)→F(V)
由此变换,就可以得到综合评价的结果 B = A ⋅ R B=A·R B=A⋅R
( B 1 × m = A 1 × n ⋅ R n × m B_{1×m}=A_{1×n}·R_{n×m} B1×m=A1×n⋅Rn×m)
综合后的评判可以看作是V上的模糊向量,记为 B = [ b 1 , b 2 , … , b m ] B=[b_1,b_2,…,b_m] B=[b1,b2,…,bm]
b1:要评价对象对评语1(v1)的隶属度
b2:要评价对象对评语2(v2)的隶属度
bm:要评价对象对评语m(vm)的隶属度
最后求得 m a x { b 1 , b 2 , … , b m } = b k max\{b_1,b_2,…,b_m\}=b_k max{b1,b2,…,bm}=bk,则要评价的对象要划分到评语k(vk)这一类。
举例
某单位对员工的年终综合评定
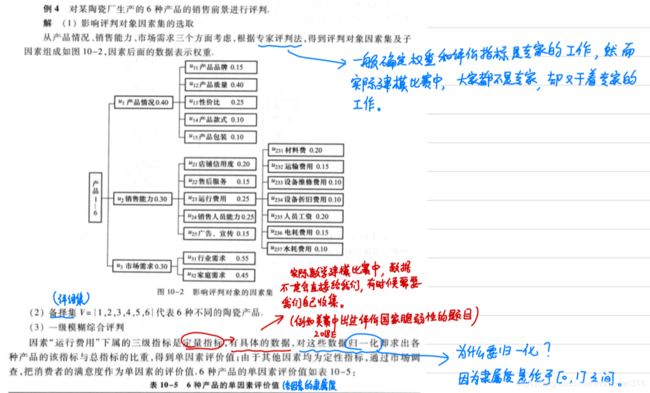
(1)取因素集U={政治表现u1,工作能力u2,工作态度u3,工作成绩4}。
(2)取评语集V={优秀v1,良好v2,一般v3,较差v4,差v5}。
(3)确定各因素的权重A=[0.25,0.2,0.25,0.3]。
(4)确定模糊综合评价矩阵,对每个因素ui做出评价。
- u1比如由群众评议打分来确定:
R1=[0.1,0.5,0.4,0,0]
上式表示,参与打分的群众中,有10%的人认为政治表现优秀,50%认为政治表现良好,40%认为政治表现一般,认为政治表现较差或差的人为0。用同样的因素进行评价。(隶属度的确定,采用模糊统计法)
- u2,u3由部门领导打分来确定
R2=[0.2,0.5,0.2,0.1,0]
R3=[0.2,0.5,0.3,0,0] - u4由单位考核组成员打分来确定:
R4=[0.2,0.6,0.2,0,0]
以Ri为第i行构成评价矩阵
R = [ 0.1 0.5 0.4 0 0 0.2 0.5 0.2 0.1 0 0.2 0.5 0.3 0 0 0.2 0.6 0.2 0 0 ] R= \left[ \begin{matrix} 0.1& 0.5 & 0.4& 0&0 \\ 0.2 & 0.5 & 0.2& 0.1&0 \\ 0.2 & 0.5 & 0.3& 0&0 \\ 0.2 & 0.6 & 0.2& 0&0 \\ \end{matrix} \right] R=⎣⎢⎢⎡0.10.20.20.20.50.50.50.60.40.20.30.200.1000000⎦⎥⎥⎤
(5)模糊综合评判
进行矩阵合成运算:
B=A·R=[0.175,0.53,0.275,0.02,0]
数值最大的评语作为综合评判的结果,则评价结果为“良好”。
空气质量评定
下表给出了大气污染物评价标准,今测得某日某地表中这些污染物日均浓度依次为:(0.07,0.20,0.123,5.00,0.08,0.14)
各污染物权重确定如下:(0.1,0.2,0.3,0.3,0.05,0.05)[权重集合A]
试评价当天空气质量等级
 从表中可以得出污染物是因素集U,且n=6,Ⅰ级、Ⅱ级、Ⅲ级、Ⅳ级是评语集V,且m=4
从表中可以得出污染物是因素集U,且n=6,Ⅰ级、Ⅱ级、Ⅲ级、Ⅳ级是评语集V,且m=4
然后采用梯形分布(一般梯形分布最为简单)求出污染物对空气质量的隶属函数
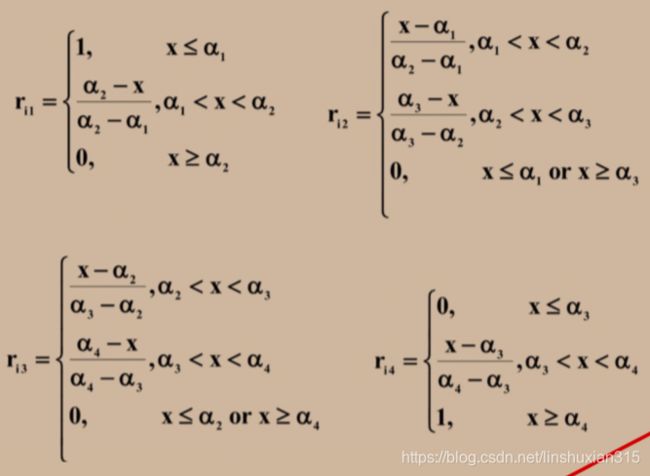 计算SO2,Ⅰ级为偏小型,Ⅱ级、Ⅲ级为中间型,Ⅳ级为偏大型,构建SO2对于四个等级的隶属函数
计算SO2,Ⅰ级为偏小型,Ⅱ级、Ⅲ级为中间型,Ⅳ级为偏大型,构建SO2对于四个等级的隶属函数
A 1 = { 1 , x < = 0.05 0.15 − x 0.15 − 0.05 , 0.05 < x < 0.15 0 , x > = 0.15 A_1=\left\{ \begin{aligned} &1 ,x<=0.05\\ &\\ & \frac{0.15-x}{0.15-0.05},0.05
A 2 = { 0 , x < = 0.05 x − 0.05 0.15 − 0.05 , 0.05 < x < = 0.15 0.25 − x 0.25 − 0.15 , 0.15 < x < 0.25 0 , x > = 0.25 A_2=\left\{ \begin{aligned} &0 ,x<=0.05\\ &\\ & \frac{x-0.05}{0.15-0.05},0.05
A 3 = { 0 , x < = 0.15 x − 0.15 0.25 − 0.15 , 0.15 < x < = 0.25 0.5 − x 0.5 − 0.25 , 0.25 < x < 0.5 0 , x > = 0.5 A_3=\left\{ \begin{aligned} &0 ,x<=0.15\\ &\\ & \frac{x-0.15}{0.25-0.15},0.15
A 4 = { 0 , x < = 0.25 x − 0.25 0.5 − 0.25 , 0.25 < x < 0.5 1 , x > = 0.5 A_4=\left\{ \begin{aligned} &0 ,x<=0.25\\ &\\ & \frac{x-0.25}{0.5-0.25},0.25
(等号在哪边无所谓)
将SO2的浓度代入得0.07,得
A1(0.07)=0.8
A2(0.07)=0.2
A3(0.07)=0
A4(0.07)=0
R1=[0.8,0.2,0,0]
这里使用梯形分布得到四个评语的隶属度的和恰好为1,使用其他分布不一定为1
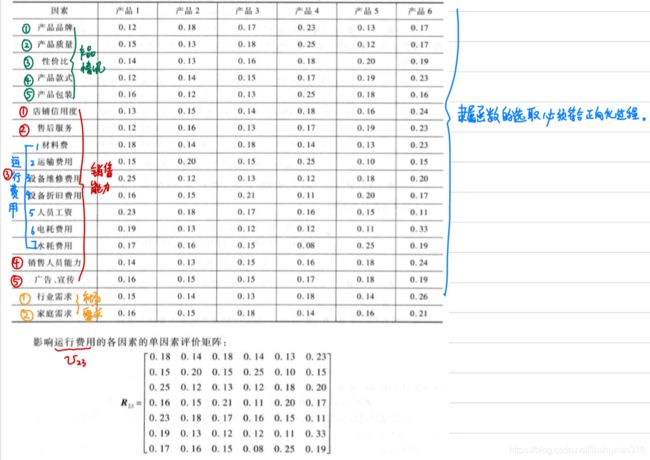
同理可得其他因素的隶属度,将隶属度按行排列得到综合评判矩阵
R = [ 0.8 0.2 0 0 0.56 0.44 0 0 0 0.6 0.4 0 0 0.5 0.5 0 0.7 0.3 0 0 0.5 0.5 0 0 ] R= \left[ \begin{matrix} 0.8& 0.2 & 0& 0 \\ 0.56 & 0.44 & 0& 0\\ 0 & 0.6 & 0.4& 0\\ 0 & 0.5 & 0.5& 0\\ 0.7 & 0.3 & 0& 0 \\ 0.5 & 0.5 & 0& 0 \\ \end{matrix} \right] R=⎣⎢⎢⎢⎢⎢⎢⎡0.80.56000.70.50.20.440.60.50.30.5000.40.500000000⎦⎥⎥⎥⎥⎥⎥⎤
B = A ⋅ R = [ 0.252 , 0.478 , 0.27 , 0 ] B=A·R=[0.252,0.478,0.27,0] B=A⋅R=[0.252,0.478,0.27,0]
空气质量为Ⅱ级
露天煤矿的边坡设计方案
也可以用topsis方法
 因素集是:可采矿量、基建投资、采矿成本、不稳定费用、净现值
因素集是:可采矿量、基建投资、采矿成本、不稳定费用、净现值
评语集是:方案Ⅰ、方案Ⅱ、方案Ⅲ、方案Ⅳ、方案Ⅴ
首先确定隶属函数
(1)可采矿量的隶属函数 [偏大型]
因为勘探的地质储量为8800吨,故可用资源的利用函数作为隶属函数
μ A ( x ) = x 8800 μ_A(x)=\frac{x}{8800} μA(x)=8800x
(2)基建投资的隶属函数 [偏小型]
投资约束是8000万元,所以
μ B ( x ) = 1 − x 8800 μ_B(x)=1-\frac{x}{8800} μB(x)=1−8800x
(3)采矿成本的隶属函数
根据专家意见,采矿成本a1<=5.5元/吨位低成本,a2=8.0元/吨为高成本,故
μ c ( x ) = { 1 , 0 ≤ x ≤ a 1 a 2 − x a 2 − a 1 , a ≤ x ≤ a 2 0 , a 2 < x μ_c(x)=\left\{ \begin{aligned} &1 ,0≤x≤a_1\\ &\\ & \frac{a_2-x}{a_2-a_1},a_≤x≤a_2 \\ &\\ & 0,a_2
(4)不稳定费用的隶属函数
μ D ( x ) = 1 − x 200 μ_D(x)=1-\frac{x}{200} μD(x)=1−200x
(5)净现值的隶属函数(取上限15,下限0.5,采用线性隶属函数)
μ E = x − 50 1500 − 50 = x − 50 1450 μ_E=\frac{x-50}{1500-50}=\frac{x-50}{1450} μE=1500−50x−50=1450x−50
根据各隶属函数计算出5个方案所对应的不同隶属度,如下表
这样就决定了单因素评判矩阵
R = [ 0.5341 0.7614 0.6705 1 0.8636 0.3750 0.3125 0.3375 0.15 0.25 1 0.76 1 0.4 0.48 0.85 0.75 0.8 0 0.2 1 0.4480 0.6552 0 0.0345 ] R= \left[ \begin{matrix} 0.5341& 0.7614 &0.6705& 1& 0.8636 \\ 0.3750 & 0.3125 &0.3375& 0.15& 0.25\\ 1 & 0.76 & 1&0.4& 0.48\\ 0.85 & 0.75 &0.8& 0& 0.2\\ 1& 0.4480 & 0.6552& 0&0.0345 \\ \end{matrix} \right] R=⎣⎢⎢⎢⎢⎡0.53410.375010.8510.76140.31250.760.750.44800.67050.337510.80.655210.150.4000.86360.250.480.20.0345⎦⎥⎥⎥⎥⎤
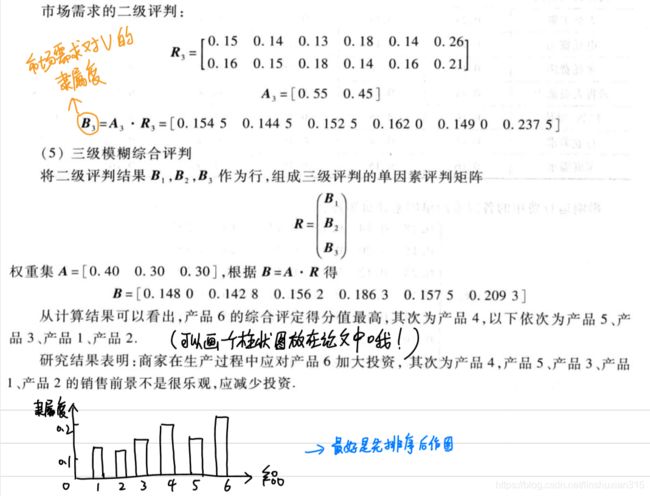
根据专家评价(如果没有专家评价,采用熵权法),诸因素在决策中占的权重为A=[0.25,0.20,0.20,0.10,0.25]
于是得诸方案的综合评价为B=A·R=[0.7435,0.5919,0.6789,0.3600,0.3905]
由此可知:方案Ⅰ最佳,Ⅲ次之,Ⅳ最差。
多级模糊综合评价模型
引入多级的原因
因素集中元素较多时,我们可以对其进行归类,归类后可以简化我们的计算。确定权重时,指标越少越容易。
二级模糊综合评价模型
操作步骤
举例
因素集U={专业课成绩、非专业课成绩、国家级竞赛成绩、省级竞赛成绩
校级竞赛成绩、国家级荣誉奖项、省级荣誉奖项、校级荣誉奖项、志愿服务时长}
用模糊统计法,十个评委投票,只看专业课成绩八个评委认为可获得一等奖学金,两个评委认为可获得二等奖学金,则这位同学的专业课对于v1的隶属度为0.8,对于v2的隶属度为0.2,对于v3的隶属度为0。同理,只看非专业课,有七位评委认为可获七等奖学金,三为评委认为可获二等奖学金。
- 若投票得到
R 1 = [ 0.8 0.2 0 0.7 0.3 0 ] R_1= \left[ \begin{matrix} 0.8 & 0.2 & 0\\ 0.7&0.3&0\\ \end{matrix} \right] R1=[0.80.70.20.300]
B 1 = [ 0.6 , 0.4 ] ⋅ R 1 = [ 0.76 , 0.24 , 0 ] B_1=[0.6,0.4]·R_1=[0.76,0.24,0] B1=[0.6,0.4]⋅R1=[0.76,0.24,0]
0.76表示只看学习成绩,可获一等奖学金的隶属度;
0.24表示只看学习成绩,可获二等奖学金的隶属度;
0表示只看学习成绩,可获三等奖学金的隶属度。
- 类似的,投票得到
R 2 = [ 0 0 1 0.5 0.5 0 0 0.6 0.4 ] R_2= \left[ \begin{matrix} 0 & 0 & 1\\ 0.5&0.5&0\\ 0&0.6&0.4\\ \end{matrix} \right] R2=⎣⎡00.5000.50.6100.4⎦⎤
B 2 = [ 0.5 , 0.3 , 0.2 ] ⋅ R 2 = [ 0.15 , 0.27 , 0.58 ] B_2=[0.5,0.3,0.2]·R_2=[0.15,0.27,0.58] B2=[0.5,0.3,0.2]⋅R2=[0.15,0.27,0.58]
0.15表示只看学习成绩,可获一等奖学金的隶属度;
0.27表示只看学习成绩,可获二等奖学金的隶属度;
0.58表示只看学习成绩,可获三等奖学金的隶属度。
-
同理可以得到
B 3 = [ 0.4 , 0.2 , 0.4 ] B_3=[0.4,0.2,0.4] B3=[0.4,0.2,0.4]
B 4 = [ 0.1 , 0.8 , 0.1 ] B_4=[0.1,0.8,0.1] B4=[0.1,0.8,0.1]
那么,构造
R 2 = [ B 1 B 2 B 3 B 4 ] = [ 0.76 0.24 0 0.15 0.27 0.58 0.4 0.2 0.4 0.1 0.8 0.1 ] R_2= \left[ \begin{matrix} B_1\\ B_2\\ B_3\\ B_4\\ \end{matrix} \right]= \left[ \begin{matrix} 0.76 & 0.24 & 0\\ 0.15&0.27&0.58\\ 0.4&0.2&0.4\\ 0.1&0.8&0.1\\ \end{matrix} \right] R2=⎣⎢⎢⎡B1B2B3B4⎦⎥⎥⎤=⎣⎢⎢⎡0.760.150.40.10.240.270.20.800.580.40.1⎦⎥⎥⎤
由于A=[0.4,0.3,0.2,0.1]
则B=A·R=[0.439,0.297,0.264] -
得出结论:获得一等奖学金的隶属度最大,该同学应被评为一等奖学金。
假设一等奖学金名额有限,那么将一等奖学金隶属度从大到小选出相应数量的同学