双指针算法(更新中....)
双指针算法
双指针算法顾名思义就是采用左右指针,对数组、字符串进行查找或排序。常见的采用双指针算法方式有以下几个
从中间向两边进行扩散,两边向中间进行集合。
快速排序
基本思想
- 找到数组中最中间的数值,以该数值为基点,大于该值则放在右侧,反之,左侧。
- 然后利用递归的思想再将左序列当成一个完整的序列再进行排序。
- 同样把序列的右侧也当成一个完整的序列进行排序。
- 直到数组长度 <= 1,返回该数组。
有三种方法可以实现
- 借助俩数组空间
- Lomuto partition scheme
- Hoare partition scheme
这里主要是使用第三种方法(双指针),其他两种方法可以看这里
https://github.com/Haohao-555/interview/blob/main/7%E6%9C%88/%E7%AC%94%E8%AE%B0.md
思路:以挖萝卜填坑为例子实现该算法
规则:
-
首先,一连串待排序的数值指的是该排萝卜的大小。
-
两个工人A、B分别站在并排萝卜的最左侧和最右侧。
-
确定填坑的判断依据
- 以挖出最左边的萝卜为基准值。
- A 为 B 填坑的标准是 挖到的萝卜必须比基准值大,才可为 B 填坑。
- B 为 A 填坑,则比基准值小。
-
两工人挖萝卜的方向,及其萝卜是否符合规则。
- A :从左到右,并且该萝卜必须在 B 的左侧。
- B:从右到左,并且该萝卜必须在 A 的右侧。
-
谁先开始:
-
一方坑为空时,另外一方先开始为其填坑。
-
根据前面几点要求,此时 A 所站位置为坑,B为其填坑。
-
-
什么时候结束:
俩个工人相遇,则结束该次填坑。
- 并且相遇位置必定为坑。
- 把一开始挖出来的萝卜给填到该坑上。可以看到以该位置为基准,左侧都小于该值,右侧都大于该值。
- 到这里,需要以相遇位置,将其分割成左侧和右侧萝卜,再分别完成两侧的萝卜游戏。
- 已此类推,直到开始填坑前判断起始位大于等于结束位,则说明萝卜已排好序。
游戏开始:
function quicksort(arr, left, right) {
let len = arr.length;
// 起始位
left = typeof left !== 'number' ? 0 : left;
// 结束位
right = typeof right !== 'number' ? len - 1 : right;
// 两者相遇
if (left >= right) return
// 挖出最左边萝卜
let value = arr[left]
// 工人 A 所站位置
let A = left;
// 工人 B 所站位置
let B = right;
// 两人没有相遇
while (A < B) {
// 此时 工人 A 位置是一个空坑
// B从右往左找比 最左边(value)小的萝卜,并且其位置正在工人 A 的右侧
while (B > A && arr[B] >= value) {
B--;
}
// B 找到啦,把该位置的萝卜挖个 工人 A 进行填坑
arr[A] = arr[B];
// 此时 工人 B 位置是一个空坑
// A从左往右找比 最左边(value)大的萝卜,并且其位置正在工人 B 的左侧
while (A < B && arr[A] <= value) {
A++;
}
// A 找到啦 该位置的萝卜挖个 工人 B 进行填坑
arr[B] = arr[A];
// 此时 工人 A 位置是一个空坑
// 如果俩工人没有相遇,则再次为对方填坑
}
/*
该次填坑结束,此时 工人A、工人B(A == B)相遇,并且该位置为空,将一开始挖出来的萝卜 (value)放到该位置上
此时形成的结果是:相遇位置的左侧都小于 value,右侧都大于 value
*/
arr[A] = value;
// 在相遇位置作为分隔点,将其分割成俩个数组,在进行递归
// 左侧萝卜
quicksort(arr, left, A);
// 右侧萝卜
quicksort(arr, A + 1, right);
}
let arr1 = [];
let arr2 = [];
for (let i = 0; i < 300000; i++) {
let num = Math.floor(Math.random() * (10000 - 1) + 1);
arr1.push(num)
arr2.push(num)
}
console.time()
quicksort(arr1)
console.timeEnd()
console.log(arr1)
console.log("----------------")
console.time()
arr2.sort((a, b) => a - b)
console.timeEnd()
console.log(arr2)
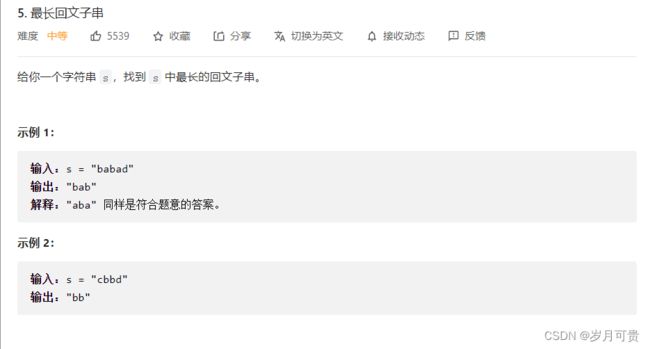
最长回文子串
解法:双指针
回文子串分为两种
- 奇数子串 aba
- 偶数子串 abba
取中心点向俩边扩散
- 奇数中心点 左:i 右:i
- 偶数中心点 左:i 右:i+1
let longestPalindrome = function (s) {
let max = "";
for (let i = 0; i < s.length; i++) {
// 奇数子串
helper(i, i);
// 偶数子串
helper(i, i+1);
}
function helper(l, r) {
// 找左右相同字符串
while (l >= 0 && r < s.length && s[l] == s[r]) {
l--;
r++;
}
// 找到回文子串后,由于 while 再执行了一轮循环,故需要对指针进行回退,即 (l + 1) (r - 1)
const maxStr = s.slice(l + 1, r + 1 - 1);
if (maxStr.length > max.length) max = maxStr;
}
return max;
}
let s = "abbaabbaaccaabbaab";
console.log(longestPalindrome(s));
盛最多水的容器
- 从两端位置向中间靠拢,计算当前面积。
- 比较当前两端高度值,高度小的一边向中间靠拢。
- 当两端重合时,结束,输出最大面积
function test(arr) {
let l = 0;
let r = arr.length - 1;
let max = 0;
while(l < r) {
let maxArea = (r - l) * Math.min(arr[l], arr[r]);
if (maxArea > max) max = maxArea;
arr[l] < arr[r] ? l++ : r--;
}
return max;
}
最接近的三数之和
- 对数组进行升序排序
- 遍历数组,从第 i 点开始作为三个值的其中一个,将左指针定位到第 i + 1,右指针定位到 nums.length - 1;
- 每次遍历,计算当前三者值,与目标值(target)更接近则保存该值
- 比目标值小,则左指针右移。
- 比目标值大,则右指针左移。
/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var threeSumClosest = function(nums, target) {
// 升序排
nums.sort((a, b) => a - b);
// 假设前三最接近目标值
let ans = nums[0] + nums[1] + nums[2];
for (let i = 0; i < nums.length; i++) { // 遍历数组
let l = i + 1; // 左指针
let r = nums.length - 1; // 右指针
while(l < r) {
// 计算此轮循环的当前值
let sum = nums[i] + nums[l] + nums[r];
// 比较,谁更接近目标值
if (Math.abs(target - sum) < Math.abs(target - ans)) ans = sum;
// 比目标值大
if (sum > target) r--;
// 比目标值小
else if (sum < target) l++;
// 等于目标值,直接返回
else return ans
}
}
return ans;
};
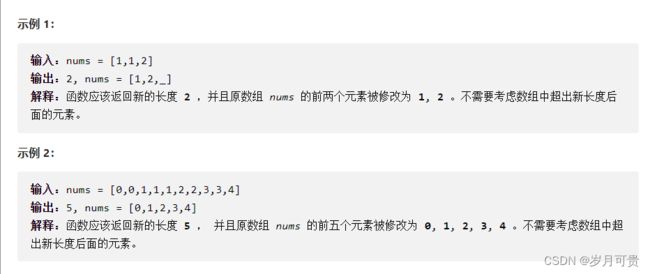
删除数组中重复的数字
起始点:俩指针都从数组下标为1开始
结束标志:到达数组尾部
slow 所指位置代表从 0 ~ (slow - 1) 没有重复的数字,slow位置代表当前可能需要被替换
fast 代表下一个数字
/**
* @param {number[]} nums
* @return {number}
*/
var removeDuplicates = function(nums) {
let len = nums.length;
if (len == 0) return [];
let fast = 1;
let slow = 1; // 待替换位置
while (fast < len) {
if (nums[fast] !== nums[fast - 1]) {
// 当前 slow 前(包括slow)都不重复
nums[slow] = nums[fast];
// 指向下一个待替换位置
++slow;
}
// 继续前进
++fast;
}
return slow
};
移除元素
var removeElement = function(nums, val) {
const n = nums.length;
let left = 0;
for (let right = 0; right < n; right++) {
if (nums[right] !== val) {
nums[left] = nums[right];
left++;
}
}
return left;
};
搜索插入位置
var searchInsert = function(nums, target) {
const n = nums.length;
let left = 0, right = n - 1, ans = n;
while (left <= right) {
let mid = ((right - left) / 2) + left;
if (target <= nums[mid]) {
ans = mid;
right = mid - 1;
} else {
left = mid + 1;
}
}
return ans;
};
更新中…