Parallel Diffusion Models of Operator and Image for Blind Inverse Problems

盲逆问题算子和图像的并行扩散模型

论文链接：https://arxiv.org/abs/2211.10656

项目链接：https://github.com/BlindDPS/blind-dps

Abstract

在正向算子已知的情况下(即非盲)，基于扩散模型的逆问题求解器已经展示了最先进的性能。然而，该方法对盲逆问题的适用性还有待探索。 在这项工作中，我们证明我们确实可以通过为前向算子构造另一个扩散先验来解决一系列盲逆问题。具体来说，在中间阶段梯度引导下的平行反向扩散可以同时优化正演算子参数和图像，从而在平行反向扩散过程结束时对两者进行联合估计。我们展示了我们的方法在两个代表性任务上的有效性-盲去模糊和通湍流成像-并表明我们的方法产生了最先进的性能，同时当我们知道函数形式时，也可以灵活地适用于一般的盲目逆问题。

1. Introduction

逆问题包含了科学和工程中的一系列重要问题，其目标是从正演算子产生的损坏测量中恢复潜在图像。从分类上看，它们可以分为两大类:非盲逆问题和盲逆问题。前者考虑了前向运算符已知的情况，因此简化了问题。而后者考虑的是算子未知的情况，需要在对潜图像重建的同时对算子进行估计。后一个问题比前一个问题困难得多，因为联合最小化通常不太稳定。

在这项工作中，我们主要关注利用生成先验来解决成像中的逆问题。在许多不同的生成模型类别中，扩散模型已经建立了新的技术。在扩散模型中，我们定义了前向数据噪声过程，该过程逐渐将图像破坏为高斯白噪声。生成过程定义为该过程的逆过程，其中逆扩散的每一步都由分数函数[53]控制。随着近年来扩散模型的兴起，文献已经证明扩散模型不仅是强大的生成模型，而且是求解逆问题的优秀生成先验。也就是说，可以通过对测量子空间的迭代投影[13,53]，或者估计后验抽样[11]来得到满足数据一致性的可行解。对于线性[13,27,53]和一些非线性[11,51]逆问题，指导无条件扩散模型解决下游逆问题的性能甚至比完全监督的模型更强。

然而，目前的解算器严格限于前向算子已知且固定的情况。例如，[11,27]考虑使用已知核的非盲去模糊。现在问题归结为只对潜在图像进行优化，因为可能性可以健壮地计算出来。不幸的是，在现实世界的问题中，确切地知道核是不切实际的。通常情况下，核也是未知的，我们必须联合估计图像和核。在这种情况下，我们不仅需要图像的先验模型，还需要一些合适的核先验模型[41,55]。尽管传统方法利用了基于patch的先验[55]、稀疏性先验[41]等方法，但它们往往无法准确地模拟分布。

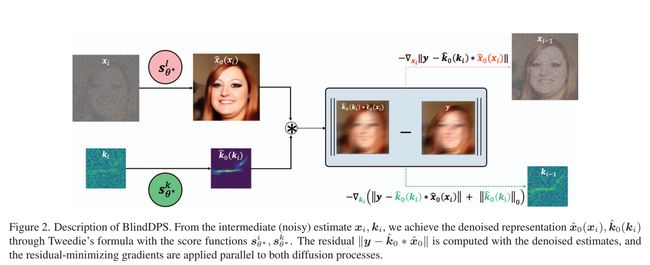
在这项工作中，我们的目标是利用扩散模型作为强生成先验的能力，并提出盲扩散后验抽样(Blind diffusion Posterior Sampling)——构建多个扩散过程来学习每个组件的先验——即使在算子未知的情况下也能进行后验抽样。BlindDPS首先用高斯噪声初始化图像和算子参数。两种模型的反向扩散是并行进行的，其中路径之间的串扰是从近似似然和测量中强制执行的，如图2所示。在我们的方法中，图像和核都是从粗估计开始的，随着$t\to 0$逐渐接近真实值(见图1©)。

事实上，我们的方法可以被认为是一种自然允许高斯尺度空间表示的粗到细策略[29,36]，这可以被看作是大多数基于优化的方法所采用的粗到细优化策略的连续推广[41,44]。此外，我们的方法一般适用于我们先验地知道前向模型结构的情况(例如卷积)。为了证明其普遍性，我们进一步证明了我们的方法也可以应用于湍流成像。从我们的实验中，我们表明所提出的方法产生了最先进的性能，同时可推广到不同的逆问题。

2. Background

扩散模型 方差保持(VP)扩散模型(即DDPM[21])，在基于分数的视角[53]中，用线性随机微分方程(SDE)定义数据$\mathbf{x}(t)\stackrel{\Delta }{=}{\mathbf{x}}_t,t\in [0,1]$的前向噪声过程。
$$d\mathbf{x}=-\frac{\beta (t)}{2}\mathbf{x}dt+\sqrt{\beta (t)}d\mathbf{w},\text{\hspace{1em}(1)}$$
其中$\beta (t)$为噪声表，$w$为标准布朗运动。我们可以定义一个适当的噪声表$\beta (t)$，使数据分布$x(0)\sim p_0=p_{data}$被模塑成标准高斯分布$x(1)\sim p_1\simeq \mathcal{N}(0,\mathbf{I})$，然后用[2]给出相应的反向SDE
$$d\mathbf{x}=\left[-\frac{\beta (t)}{2}\mathbf{x}-\beta (t){\nabla }_{{\mathbf{x}}_t}\log p_t({\mathbf{x}}_t)\right]dt+\sqrt{\beta (t)}d\bar{\mathbf{w}},\text{\hspace{1em}(2)}$$
其中$\nabla x_t\log p_t(x_t)$是分数函数，通常通过去噪分数匹配(DSM) [56]
$${\theta }^{\ast }=\underset{\theta }{\mathrm{argmin}}{\mathbb{E}}_{t,{\mathbf{x}}_t,{\mathbf{x}}_0}\left[\Vert s_{\theta }({\mathbf{x}}_t,t)-{\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t|{\mathbf{x}}_0){\Vert }_2^2\right].\text{\hspace{1em}(3)}$$
训练完成后，我们可以对公式(2)中的反向扩散使用插入式估计$\nabla x_t\log p_t(x_t)\sim s_{\theta }(x_t,t)$，并通过离散化(如[21]的祖先采样)求解，有效地从先验分布$p(x_0)$中采样。

扩散后验抽样(DPS) 考虑以下高斯测量模型
$$p(\mathbf{y}|{\mathbf{x}}_0)=\mathcal{N}(\mathbf{y}|\mathcal{H}({\mathbf{x}}_0),{\sigma }^2\mathbf{I}),\mathbf{y}\in {\mathbb{R}}^m,{\mathbf{x}}_0\in {\mathbb{R}}^n,\text{\hspace{1em}(4)}$$
其中$y$是损坏的测量值，$x_0$是我们希望估计的潜在图像，$\mathcal{H}$是正演算子。由于问题通常是病态的，因此希望能够从后验分布$p(x_0|y)$中抽样。根据贝叶斯规则，对于一般的时间步长$t$，
$$\begin{array}{rl}{\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t|\mathbf{y})& ={\nabla }_{{\mathbf{x}}_t}\log p(\mathbf{y}|{\mathbf{x}}_t)+{\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t)\\ & \simeq {\nabla }_{{\mathbf{x}}_t}\log p(\mathbf{y}|{\mathbf{x}}_t)+{\mathbf{s}}_{{\theta }^{\ast }}({\mathbf{x}}_t,t),\end{array}\text{\hspace{1em}(5)(6)}$$
我们可以将公式(6)代入反向扩散公式(2)中，从$p(x_0|y)$中采样，即
$$\begin{array}{rl}d\mathbf{x}& =(-\frac{\beta (t)}{2}\mathbf{x}-\beta (t)[{\nabla }_{{\mathbf{x}}_t}\log p(\mathbf{y}|{\mathbf{x}}_t)\\ & +{\mathbf{s}}_{{\theta }^{\ast }}({\mathbf{x}}_t,t)])dt+\sqrt{\beta (t)}d\bar{\mathbf{w}}.\end{array}\text{\hspace{1em}(7)}$$
注意，时间条件的对数似然对数$p(y|x_t)$通常是难以处理的。然而，在DPS[11]的工作中表明，我们可以使用近似值来达到
$${\nabla }_{{\mathbf{x}}_t}\log p_t(\mathbf{y}|{\mathbf{x}}_t)\simeq {\nabla }_{{\mathbf{x}}_t}\log p(\mathbf{y}|{\hat{\mathbf{x}}}_0({\mathbf{x}}_t)),$$
其中
$${\hat{x}}_0(x_t):=\frac{1}{\sqrt{\bar{\alpha }(t)}}(x_t+(1-\bar{\alpha }(t))s_{{\theta }^{\ast }}(x_t,t))\text{\hspace{1em}(8)}$$
是由Tweedie公式[17]给出的VP-SDE上下文中$x_t$的去噪估计。因此，可以使用以下易于处理的反向SDE从后验分布中抽样
$$\begin{array}{r}d\mathbf{x}=(-\frac{\beta (t)}{2}\mathbf{x}-\beta (t)[{\nabla }_{{\mathbf{x}}_t}\log p(\mathbf{y}|{\hat{\mathbf{x}}}_0({\mathbf{x}}_t))\\ +{\mathbf{s}}_{{\theta }^{\ast }}({\mathbf{x}}_t,t)])dt+\sqrt{\beta (t)}d\bar{\mathbf{w}},\end{array}\text{\hspace{1em}(9)}$$
其中我们观察到${\nabla }_{{\mathbf{x}}_t}\log p(\mathbf{y}|{\hat{\mathbf{x}}}_0({\mathbf{x}}_t))$可以使用解析似然有效地计算，并通过分数函数反向传播，即
$${\nabla }_{{\mathbf{x}}_t}\log p_t({\mathbf{x}}_t|\mathbf{y})\simeq s_{{\theta }^{\ast }}({\mathbf{x}}_t)-\frac{1}{{\sigma }^2}{\nabla }_{{\mathbf{x}}_t}\Vert \mathbf{y}-\mathcal{H}({\hat{\mathbf{x}}}_0({\mathbf{x}}_t)){\Vert }_2^2.$$
但需要注意的是，公式(9)中的方法仅适用于正向模型$\mathcal{H}$固定的情况，因此不能直接用于求解盲逆问题。

盲逆问题 盲逆问题考虑正向模型$\mathcal{H}$未知的情况。其中，我们重点研究了正向算子用$\phi$参数化的情况，我们需要对参数$\phi$进行估计。具体来说，考虑以下正向模型
$$y={\mathcal{H}}_{\phi }(x)+n,\text{\hspace{1em}(10)}$$
其中$\phi$为正向模型的参数，$x$为ground truth图像，$n$为某种噪声。这里，$\phi$和$x$都是未知的，应该进行估计。求解公式(10)的一种经典方法是针对以下问题进行优化
$$\underset{\mathbf{x},\mathbf{\phi }}{\min }\frac{1}{2}\Vert {\mathcal{H}}_{\mathbf{\phi }}(\mathbf{x})-\mathbf{y}{\Vert }^2+R_{\mathbf{\phi }}(\mathbf{\phi })+R_{\mathbf{x}}(\mathbf{x}),\text{\hspace{1em}(11)}$$
其中$R_{\phi }(\phi )$， $R_x(x)$分别是$\phi$， $x$的正则化函数，也可以认为是每个分布的负对数先验，例如$R(\cdot )=-\log p(\cdot )$。

例如，考虑如图3(a)所示的相机运动模糊的盲反卷积。正向模型为
$$y=k\ast x+n,\text{\hspace{1em}(12)}$$
其中k为模糊核，对应参数φ。另一方面，虽然由于波传播理论的高度复杂性，大气湍流的“真实”正向模型很少在实践中直接使用，但经常使用倾斜模糊模型[5,6,49]，如 该模型很简单但相当准确。

具体而言，该成像过程的可视化如图3(b)所示，可以用
$$y=k\ast {\mathcal{T}}_{\varphi }(x)+n,\text{\hspace{1em}(13)}$$
其中$\mathcal{T}$为倾斜算子，由倾斜向量场$\phi$参数化。为了消除核和图像之间的尺度模糊，通常使用核的大小和极性约束：
$$1^{T}k=1,k⪰0.\text{\hspace{1em}(14)}$$
那么，在约束公式(14)下，正向模型公式(12)或公式(13)的优化算法公式(11)的成功取决于两个因素：1)先验施加函数$Rx,k$对真实先验的估计有多接近，以及2)优化过程找到最小值的程度。传统方法在这两个方面都不是最优的。首先，先验函数(如稀疏度[41]，暗通道[44]，从深度网络隐式[47])不能完全代表真实的先验。其次，优化过程不稳定，难以调优。例如，[41,44]需要每张图像不同的加权参数，并且在粗精优化策略的阶段过渡突变时经常失败。在第3节中，我们将展示我们的方法可以解决这两个问题。

3. BlindDPS

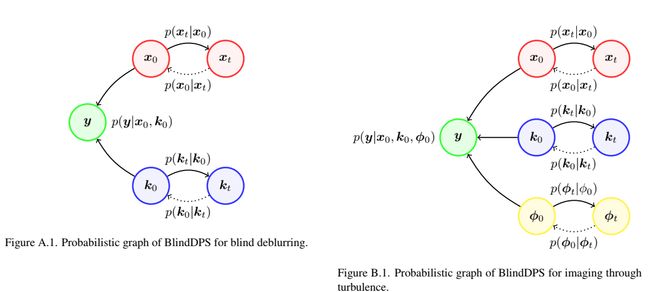
在DPS[11]中，作者通过训练一个模拟$\nabla x\log p(x)$的分数函数来使用$R_x$的扩散先验。对于盲逆问题，还需要指定参数$p(\varphi )$的先验模型。在这方面，我们的建议是通过估计$\nabla \phi \log p(\phi )$来对正向模型参数使用扩散先验。有了这样的选择，与传统的选择相比，人们可以为参数建立一个更准确的先验模型。在下文中，我们详细介绍了如何构建BlindDPS方法，重点是盲反卷积。通过湍流成像的方法可以用完全类似的方式推导出来，其细节可在补充部分B.1中找到。

关键想法。在盲去模糊(反卷积)中，概率正向模型规定如下
$$p(\mathbf{y}|{\mathbf{x}}_0,{\mathbf{k}}_0):=\mathcal{N}(\mathbf{y}|{\mathbf{k}}_0\ast {\mathbf{x}}_0,{\sigma }^2\mathbf{I}),\text{\hspace{1em}(15)}$$
其中$k_0$是卷积核的随机变量。由于$x_0$和$k_0$是独立的，后验概率为
$$p({\mathbf{x}}_0,{\mathbf{k}}_0|\mathbf{y})\propto p(\mathbf{y}|{\mathbf{x}}_0,{\mathbf{k}}_0)p({\mathbf{x}}_0)p({\mathbf{k}}_0).\text{\hspace{1em}(16)}$$
请注意，我们的目标是通过$p(x_0)$和$p(k_0)$的分数函数对它们使用隐式扩散先验。我们可以很容易地对图像使用预训练的分数函数。同样，核的分数函数也可以由标准DSM(3)估计得到${\mathbf{s}}_{\theta \ast }^k(\mathbf{k},t)\simeq {\nabla }_{{\mathbf{k}}_t}\log p_t({\mathbf{k}}_t)$。请注意，执行DSM以获得${\mathbf{s}}_{\theta \ast }^k$的成本远低于训练图像评分函数${\mathbf{s}}_{\theta \ast }^i$，因为分布要简单得多，并且向量$k$的维数也足够小于$x$。

另一方面，同样从$x_0$和$k_0$的独立性出发，我们可以构造两个形式相同的反向扩散过程：
$$\begin{array}{c}dx=\left[-\frac{\beta (t)}{2}\mathbf{x}-\beta (t){\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t)\right]dt+\sqrt{\beta (t)}d\bar{\mathbf{w}},\\ d\mathbf{k}=\left[-\frac{\beta (t)}{2}\mathbf{k}-\beta (t){\nabla }_{{\mathbf{k}}_t}\log p({\mathbf{k}}_t)\right]dt+\sqrt{\beta (t)}d\bar{\mathbf{w}}.\end{array}$$
请注意，两个反向SDE只能从边缘- $p(x_0)$， $p(k_0)$进行采样。然而，我们可以从后验概率中定义$x,y$和$k$之间的依赖关系。利用公式(16)中的贝叶斯规则，我们有
$$\begin{array}{l}{\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t,{\mathbf{k}}_t|\mathbf{y})={\nabla }_{{\mathbf{x}}_t}\log p(\mathbf{y}|{\mathbf{x}}_t,{\mathbf{k}}_t)+{\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t),\\ {\nabla }_{{\mathbf{k}}_t}\log p({\mathbf{x}}_t,{\mathbf{k}}_t|\mathbf{y})={\nabla }_{{\mathbf{k}}_t}\log p(\mathbf{y}|{\mathbf{x}}_t,{\mathbf{k}}_t)+{\nabla }_{{\mathbf{k}}_t}\log p({\mathbf{k}}_t).\end{array}$$
在这里，为了估计一般情况下难以处理的时间条件对数似然$\log p(y|x_t,k_t)$，我们需要得到以下结果：

定理1。在[11]相同的条件下，我们有
$$\begin{array}{rl}{\nabla }_{{\mathbf{x}}_t}\log p_t(\mathbf{y}|{\mathbf{x}}_t,{\mathbf{k}}_t)& \simeq {\nabla }_{{\mathbf{x}}_t}\log p(\mathbf{y}|{\hat{\mathbf{x}}}_0({\mathbf{x}}_t),{\hat{\mathbf{k}}}_0({\mathbf{k}}_t))\\ {\nabla }_{{\mathbf{k}}_t}\log p_t(\mathbf{y}|{\mathbf{x}}_t,{\mathbf{k}}_t)& \simeq {\nabla }_{{\mathbf{k}}_t}\log p(\mathbf{y}|{\hat{\mathbf{x}}}_0({\mathbf{x}}_t),{\hat{\mathbf{k}}}_0({\mathbf{k}}_t)).\end{array}$$
备注1。只要$x_t，k_t$是独立的，我们的定理就成立。注意，只要建立了变量之间的独立性，该定理就可以进一步推广到处理更多的随机变量。换句话说，我们可以为前向模型的每个分量构造任意多个扩散过程，这可以类似于定理 1 中提出的近似来求解。这一结果将对我们解决补充章节B.1中的湍流成像问题有所帮助。

使用定理1，我们最终得到以下反向SDE
$$\begin{array}{rl}dx& =(-\frac{\beta (t)}{2}\mathbf{x}-\beta (t)[{\nabla }_{{\mathbf{x}}_t}\log p(\mathbf{y}|{\hat{\mathbf{x}}}_0({\mathbf{x}}_t),{\hat{\mathbf{k}}}_0({\mathbf{k}}_t))\\ & +{\mathbf{s}}_{{\theta }^{\ast }}^i({\mathbf{x}}_t,t)])dt+\sqrt{\beta (t)}d\bar{\mathbf{w}},\\ \text{dk}& =(-\frac{\beta (t)}{2}\mathbf{k}-\beta (t)[{\nabla }_{{\mathbf{k}}_t}\log p(\mathbf{y}|{\hat{\mathbf{x}}}_0({\mathbf{x}}_t),{\hat{\mathbf{k}}}_0({\mathbf{k}}_t))\\ & +{\mathbf{s}}_{{\theta }^{\ast }}^k({\mathbf{k}}_t,t)])dt+\sqrt{\beta (t)}d\bar{\mathbf{w}}.\end{array}\text{\hspace{1em}(17)(18)}$$
公式(17)，(18)的系统现在是数值可解的，因为对数似然的梯度是解析可处理的。对于高斯测量，我们有
$${\nabla }_{{\mathbf{x}}_t}\log p(\mathbf{y}|{\hat{\mathbf{x}}}_0,{\hat{\mathbf{k}}}_0)=-\frac{1}{{\sigma }^2}{\nabla }_{{\mathbf{x}}_t}\Vert \mathbf{y}-{\hat{\mathbf{k}}}_0\ast {\hat{\mathbf{x}}}_0{\Vert }_2^2.\text{\hspace{1em}(19)}$$
结合祖先采样步长[21]，我们的盲去模糊后验采样算法在算法1中正式给出。这里，请注意，我们选择用静态步长乘以范数的梯度，而不是用与时间相关的步长乘以平方范数的梯度，因为它被证明是有效的，尽管它很简单[11]。此外，为了施加通常的条件公式(14)，我们定义了一个集合$C:=\{\mathbf{k}|1^T\mathbf{k}=1,\mathbf{k}⪰0\}$，并在每个中间步骤估计了${\hat{k}}_0$之后，通过算法1中的${\mathcal{P}}_C({\hat{k}}_0)$投影到集合上。

对于所提出的方法的可视化说明，见图2。

稀疏性增强扩散先验。在正确选择$\alpha$的情况下，直接执行公式(17)、公式(18)可以得到相当稳定的结果。在这里，我们更进一步，从经典工作中吸取教训。由于我们经常希望估计稀疏的模糊核，我们仅通过用${\ell }_0/{\ell }_1$正则化增加扩散先验来提高我们正在估计的核的稀疏性。核的最小化策略变成
$$k_{i-1}=k_{i-1}^{\prime }-\alpha \left(\Vert y-{\hat{\mathbf{k}}}_0\ast {\hat{\mathbf{x}}}_0{\Vert }_2+\lambda R_{\mathbf{k}}({\hat{\mathbf{k}}}_0)\right),\text{\hspace{1em}(20)}$$
其中$\lambda$为正则化强度，$R_k(\cdot ):={\ell }_0/{\ell }_1$正则化的选择取决于数据集的类型。有了这样的增强，重建可以进一步稳定。

高斯尺度空间的解释。(高斯)尺度空间理论[36]指出，人们可以通过高斯滤波器逐渐卷积来表示多个尺度的信号。由于在扩散的前向传递中向随机向量添加高斯噪声在密度域中具有对偶关系（即与高斯核的卷积），因此可以将扩散过程视为此类过程的实现。因此，反向扩散过程可以解释为通过高斯尺度空间演化的从粗到精的综合过程，最明显的是通过$t=1\to 0$演化时的${\hat{\mathbf{x}}}_0({\mathbf{x}}_t),{\hat{\mathbf{k}}}_0({\mathbf{k}}_t)$(见图1©)。

对于盲反卷积问题，为了达到最优的质量，标准做法是在粗尺度上通过下采样开始优化过程，然后按照预先确定的时间表依次上采样以改进估计[41,42]。然而，离散化的时间表通常是突然的(例如[41,42]使用离散化)和临时的。另一方面，通过使用反向扩散过程，我们获得了一个自然的、平滑的进化时间表，这可以被认为是粗到细重建策略的连续推广。这可能是该方法能够显著优于传统方法的另一个原因。

4. Experiments

4.1. 实验装置

数据集。对于盲去模糊，我们使用FFHQ 256×256[26]和AFHQ-dog 256×256[10]。我们为FFHQ选择了1k的验证集，为AFHQ-dog选择了完整的500张测试图像。我们利用预训练的(图像)分数函数，如[13]的实验设置。对于湍流成像，我们使用FFHQ 256×256和ImageNet 256×256[15]。对于这两个盲反问题，我们都加入了σ = 0.02的高斯测量噪声。详情请参阅实验装置见附录F部分

评估。我们使用三个度量- Frechet inception距离(FID)，学习感知图像Patch相似度(LPIPS)和峰值信噪比(PSNR) -定量测量图像重建的性能。对于核估计，我们使用均方误差(MSE)和归一化卷积(MNC)最大值[23]，计算公式为
$$\mathrm{MNC}:=\max \left(\frac{\tilde{\mathbf{k}}\ast {\mathbf{k}}^{\ast }}{\Vert \tilde{\mathbf{k}}{\Vert }_2\Vert {\mathbf{k}}^{\ast }{\Vert }_2}\right),\text{\hspace{1em}(21)}$$

4.2. 结果

盲去模糊。运动去模糊结果如图1(a)和图4所示。由于我们对运动去模糊的设置施加了一个相当大的模糊核的激进退化，大多数现有技术都失败了，无法产生一个可行的解决方案。相比之下，我们的方法可以准确地捕获核和图像的清晰度。图4第三行所示的高斯去模糊也有类似的趋势。其他方法远远低于 BlindDPS，因为它们要么产生因模糊核估计不准确而模糊的重建，要么显着失败（例如 SelfDeblur）。

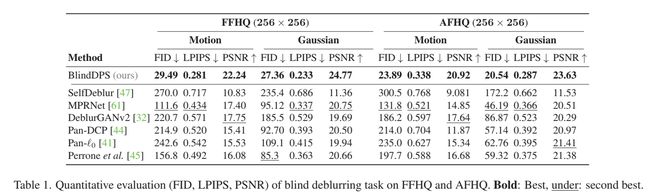
此外，所提出的方法在所有定量指标中都建立了最先进的方法，如表 1 和表 2 所示。

不同的图像和核。为了证明BlindDPS的通用性，我们将我们的方法应用于图5中更多样化的图像和核。我们看到，在所有的病例中，BlindDPS确实产生了高质量的重建。值得注意的是，当使用较小大小的核时，我们可以在推理之后简单地对推断核进行中心裁剪，而不需要任何额外的处理。

湍流成像。重建结果如图1(b)和图6所示，定量指标如表3所示。与盲去模糊的结果一致，BlindDPS在大多数情况下优于比较方法，有效地消除了测量中的模糊和倾斜。值得注意的是，我们的方法在感知度量(即FID, LPIPS)上优于所有其他方法。对于PSNR，所提出的方法通常略低于监督学习方法，这是可以预料的，因为对于严重退化的重建，检索高频细节通常会惩罚这种失真指标[3]。

4.3. 消融研究

我们进行了两项消融研究来验证我们的设计选择：1)对正向模型参数使用扩散先验，以及2)用稀疏先验增加扩散先验。有关实验设置的详细信息以及进一步的分析可以在补充部分C中找到。

正向模型的扩散先验。有人可能会问，为什么核的分数函数首先是必要的，因为人们也可以仅仅通过使用似然梯度的梯度下降来估计核。事实上，这对应于对核分布使用均匀先验，我们将其与图7中提出的扩散先验(BlindDPS)进行比较。我们清楚地看到，使用均匀先验会产生严重扭曲的结果，核估计很差。从这个实验中，我们观察到使用另一个扩散过程专门为正演模型是至关重要的性能。

稀疏度正则化的影响。在BlindDPS中做出的一个设计选择是将额外的稀疏性正则化应用于内核。在这里，我们分析了这种正则化的效果。在表C.1中，我们报告了核的定量度量，这取决于正则化权值λ。显然，设置λ = 0.0会导致较差的性能，特别是对于运动去模糊。然而，当设置λ≥0.1时，我们可以看到，无论选择的权重值如何，都可以获得良好的性能。由于扩散先验已经被证明具有惊人的高泛化能力[14,24]，我们选择一个温和的权重值λ = 1.0，它在不过度降低扩散先验影响的情况下给出了视觉上吸引人的结果。

5. Discussion and Related Works

这项工作遵循了通过扩散模型开发可以解决逆问题的方法的努力。首先开发了基于凸集迭代投影(POCS)的方法，在去噪步骤和投影步骤之间迭代[9,13,14,52,53]。提出了通过退火朗格万动力学(ALD)[24]和奇异值分解(SVD)[27]来近似后验采样的方法，后者对噪声测量具有特别的鲁棒性。

最近的趋势转向利用 Tweedie 公式在中间步骤中以各种名称利用去噪估计——流形约束梯度 (MCG) [12]、梯度引导 [22] 和基于重建的方法 [28]。 扩散后验采样（DPS）[11]是与我们的方法最相似的方法，表明这种方法是后验采样过程的近似。然而，到目前为止，没有一种方法考虑到盲逆问题，据我们所知，我们是第一个证明具有扩散尺度的盲设置的后验抽样。

局限性和未来方向。由于BlindDPS对多因素(如核、倾斜图、图像)进行联合最小化，其鲁棒性通常不如非盲重建方案。有时，当参数调优不正确时，解决方案会发散。当我们用高多样性的数据集(如ImageNet)进行实验时，这种不稳定性。由于我们发现ImageNet扩散之前是不稳定的，因此将我们的方法扩展到用于野外模糊图像是很棘手的，并且将这项工作的范围限制在模拟图像上。对于湍流成像，通常会出现倾斜图估计不正确而核和ground truth图像估计准确的情况。此外，当我们为每个组件训练和使用指定的扩散分数函数时，由于额外的向前/向后传递通过新涉及的分数函数，推理速度会延迟。当前向函数涉及到估计附加参数时，所需的分数函数的数量将线性扩展，对于复杂的函数形式来说效率不高。最后，我们注意到，我们的方法还没有解决真正的盲目情况，在这种情况下，我们不知道前向映射的函数形式。解决真正的盲案例将是未来研究的一个有趣方向。

6. Conclusion

在这项工作中，我们提出了BlindDPS，一个通过联合估计前向测量算子和待重构图像的参数来解决盲逆问题的框架。我们从理论上展示了我们如何构建一个反向SDE系统来近似盲逆问题的后验抽样，通过使用多个分数函数来估计组件的每个部分。通过大量的实验，我们表明，BlindDPS在盲去模糊和通过湍流成像方面建立了最先进的性能，即使在退化和测量噪声很大的情况下也是如此。

Supplementary Material

A. 证明

B. BlindDPS

C. 详细的消融研究

C.1. 正向模型的扩散先验

C.2. 稀疏度正则化的影响

C.3. 估算进度

D. 扩展相关工作

D.1. 盲去模糊

D.2. 湍流成像

E. 逆问题设置

盲去模糊
$$y=k_0\ast x_0+n,\mathbf{n}\sim \mathcal{N}(0,{\sigma }^2\mathbf{I}),$$
湍流成像
$$\mathbf{y}={\mathbf{k}}_0\ast {\mathcal{T}}_{{\mathbf{\varphi }}_0}({\mathbf{x}}_0)+\mathbf{n},\mathbf{n}\sim \mathcal{N}(0,{\sigma }^2\mathbf{I}),$$

F. 实验细节

F.1. 训练

我们按照[12]的设置对FFHQ数据集和ImageNet数据集采用预训练的分数函数。当训练内核的分数函数时，我们创建了一个由60k个64 × 64内核组成的数据库。其中，通过采样强度值I ~ Unif(0.2,1.0)。另外10k个高斯模糊核生成随机标准差σ ~ Unif (0.1,5.0)。为了训练kernel / tilt-map的分数函数，我们使用了guided-diffusion中的U-Net架构，并使用基本配置来训练模型。模型使用单个RTX 3090 GPU进行3.0M / 1.5M步数的训练，分别耗时1天/ 2天左右。

F.2. 计算时间

如局限性中所述，在推理时间使用的分数函数的数量与前向模型中涉及的组件数量呈线性关系。对于盲去模糊，使用两个神经网络(图像，核)，对于通过湍流成像，使用三个神经网络(图像，核，倾斜图)。为了量化每种情况下的额外计算成本，我们测量了用单个RTX 2080ti GPU重建单个图像的时钟时间。DPS: 132.39秒。BlindDPS -盲去模糊(2个评分函数)：180.22秒。BlindDPS-湍流成像(3个评分函数)：220.76秒。

F.3. 比较的方法

F.4. 数据和代码可用性

G. 进一步实验

进一步的盲去模糊实验结果如图G.1、G.2、G.3、G.4所示。进一步的湍流成像实验结果如图G.5、G.6所示。