数字信号处理、实验一 离散时间信号与系统的分析

项目一 常见离散信号的MATLAB产生和图形显示
1.实验目的
加深对常用离散信号的理解
2.实验内容
编译程序产生以下几种信号（长度可输入确定），并绘出其图形。
3.实验步骤
（1）64点单位抽样序列：
脚本程序：

N=input('输入N');
M=input('向右位移长度');
n=[0:N-1];
x=[zeros(1,M),1,zeros(1,N-M-1)];
stem(n,x);

    输入：

输入N64
向右位移长度0
结果：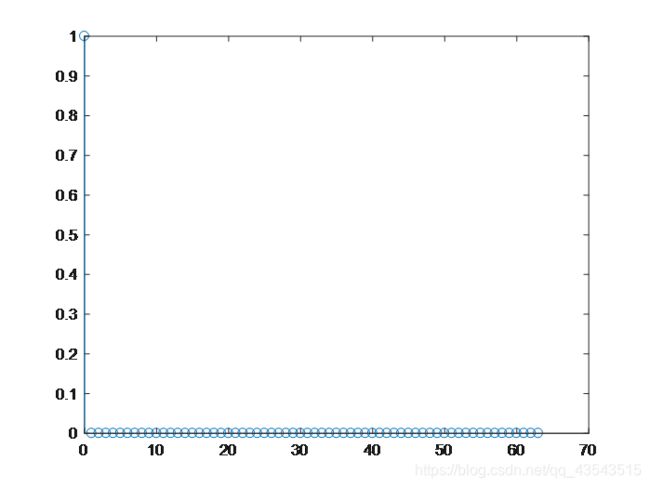
（2）64点δ(n-20)的序列：
脚本程序：

N=input('输入N');
M=input('向右位移长度');
n=[0:N-1];
x=[zeros(1,M),1,zeros(1,N-M-1)];
stem(n,x);

    输入：

输入N64
位移长度20
结果：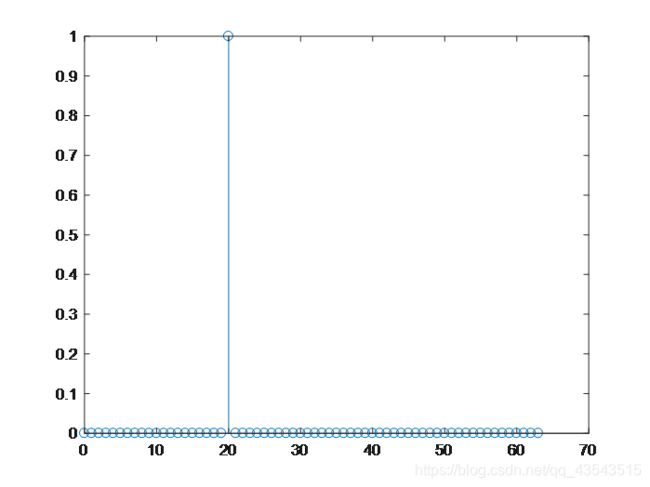
（3）任意序列f(n)=8.0δ(n)+3.4δ(n-1)+1.8δ(n-2)+5.6δ(n-3)+2.9δ(n-4)+0.7δ(n-5)：
脚本程序：

N=input('输入N=');
M=0;%初始位移长度
n=[0:N-1];
y=zeros(1,N);
for a=1:N
    C=input('输入系数（从第一项开始）=');
    x=[zeros(1,M),1,zeros(1,N-M-1)];
    y=y+C*x;
    M=M+1;
end
stem(n,y);

输入：
输入N=6
输入系数（从第一项开始）=8
输入系数（从第一项开始）=3.4
输入系数（从第一项开始）=1.8
输入系数（从第一项开始）=5.6
输入系数（从第一项开始）=2.9
输入系数（从第一项开始）=0.7
结果：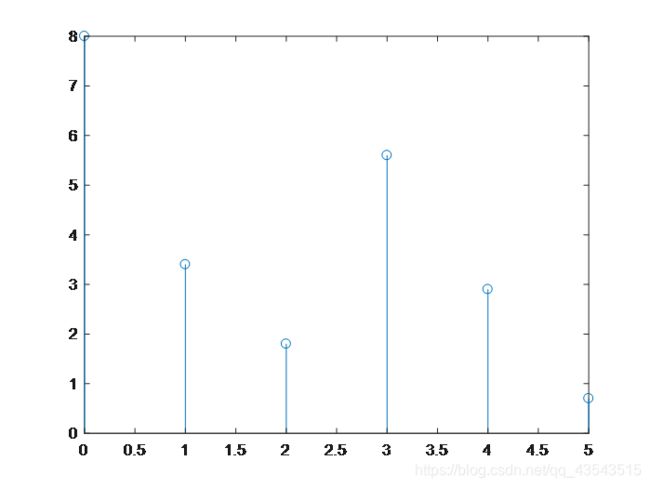
（4）32点正弦序列A=3，f=100，fs=800，fai=1.2
脚本程序：

N=input('输入N=');
A=input('A=');
f=input('f=');
fs=input('fs=');
fai=input('fai=');
n=0:N-1;
x=A*sin(2*pi*f*n/fs+fai);
stem(n,x);
输入：
输入N=32
A=3
f=100
fs=800
fai=1.2

结果：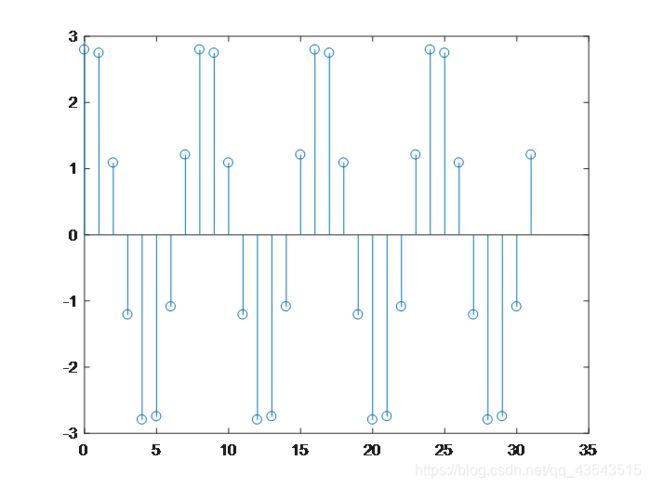
（5）32点复正弦序列A=3，ommiga=314
脚本程序：

N=input('输入N=');
A=input('A=');
ommiga=input('ommiga=');
n=0:N-1;
x=A*exp(j*ommiga*n);
y1=real(x);
figure(1)
stem(n,y1);
ylabel('实部');
y2=imag(x);
figure(2)
stem(n,y2);
ylabel('虚部');

输入：
输入N=32
A=3
ommiga=314
结果：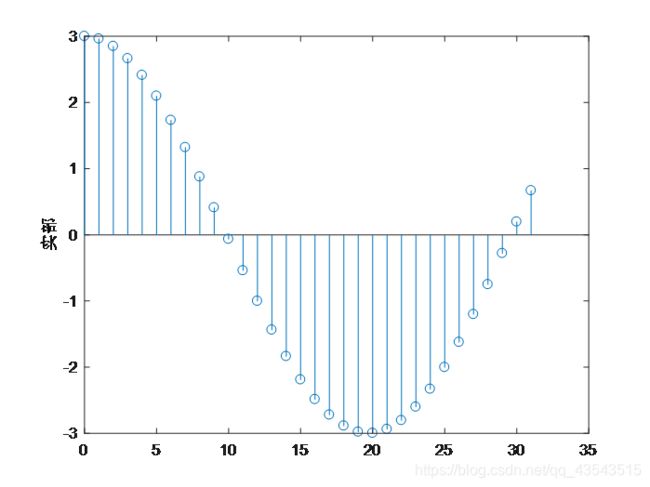

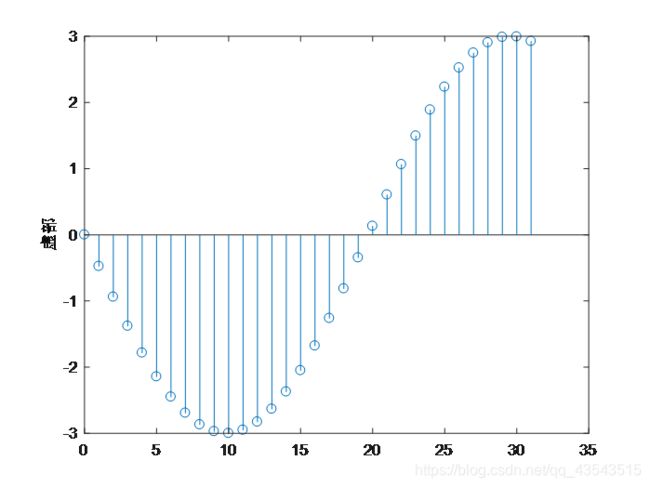
（5）32点实指数序列A=3，a=3
脚本程序：
N=input(‘输入N=’);
A=input(‘A=’);
a=input(‘a=’);
n=0:N-1;
x=A*a.^n;
stem(n,x);
输入：
输入N=32
A=3
a=0.7
结果：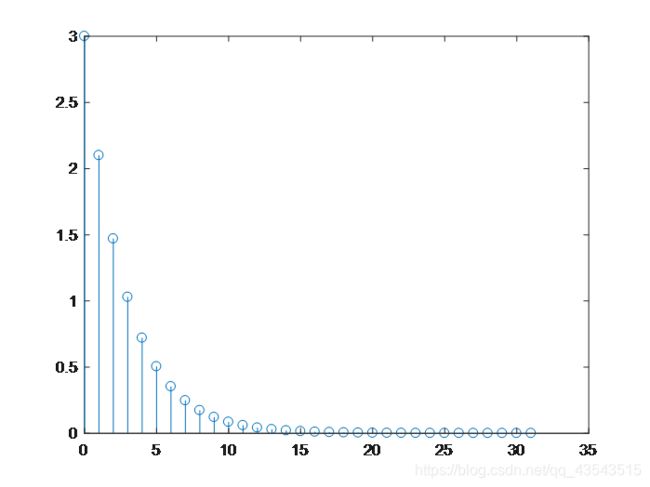
4.实验要求
讨论复指数序列的性质
实部为cos函数对应的序列，虚部为sin对应的序列