数字信号仿真实验——实验二离散时间信号与系统的频域分析

1.实验目的

（1）进一步加深DTFT、DFT和z 變化的算法原理和基本性質的理解。
（2）熟悉系統的頻率响应和传输函数。
（3）学习用FFT对时域离散信号进行谱分析的方法，了解可能出现的问题，以便在实际中正确应用FFT。

2.实验原理

（1）信号的频域表示



（2）频率响应

（3）传输函数

3.实验内容

（1）编写程序产生以下典型信号：

（2）N = 8和N= 16分别对（1）中所给出的信号逐个进行频谱分析，观察幅频特性。

4.实验报告要求

(1)在实验报告中简述实验目的和实验原理要点。
(2)在实验报告中附上实验过程记录的各典型信号的幅频特性曲线，与理论结果比较并分析误差产生的原因以及用FFT谱分析时有关参数的选择方法。
(3)总结实验中的主要结论。

Matlab程序1_1,2：

Problem1_1,2
clear
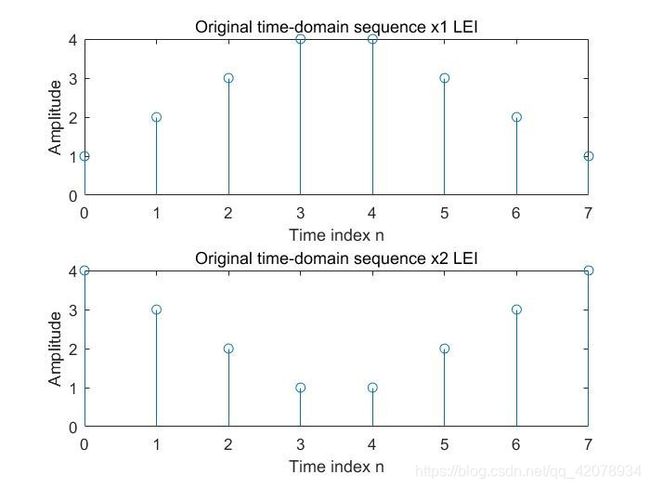
x1=[];m=0:7;x2=[];
for n=0:3;
    xa=n+1;
    xb=4-n;
    x1=[x1 xa];
    x2=[x2 xb];
end
for n=4:7;
    xa=8-n;
    xb=n-3;
    x1=[x1 xa];
    x2=[x2 xb];
end
figure(1)
subplot(211)
stem(m,x1);%%绘制火柴梗，产生离散信号
xlabel('Time index n');
ylabel('Amplitude');
title('Original time-domain sequence x1 LEI');
subplot(212)
stem(m,x2);%%绘制火柴梗，产生离散信号
xlabel('Time index n');
ylabel('Amplitude');
title('Original time-domain sequence x2 LEI');
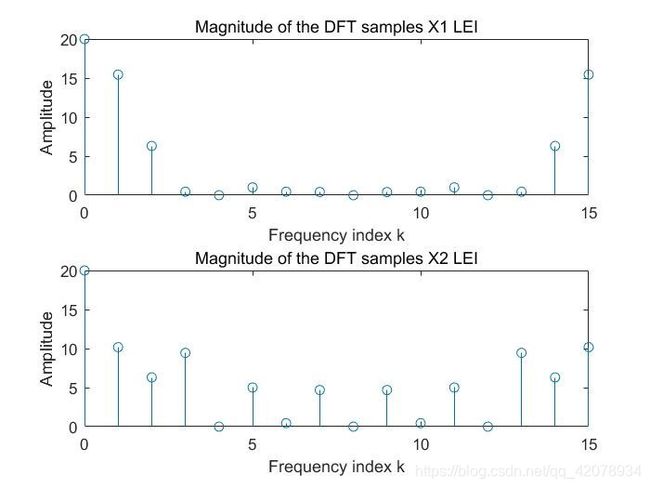
%DFT
N=input('N=');
k=0:N-1;
X1=fft(x1,N);%%傅里叶变换
X2=fft(x2,N);%%傅里叶变换
figure(2)
subplot(211)
stem(k,abs(X1));%%绘制火柴梗，产生离散信号
xlabel('Frequency index k');
ylabel('Amplitude');
title('Magnitude of the DFT samples X1 LEI');
subplot(212)
stem(k,abs(X2));%%绘制火柴梗，产生离散信号
xlabel('Frequency index k');
ylabel('Amplitude');
title('Magnitude of the DFT samples X2 LEI');

运行结果1_1,2：

Matlab程序1_3,4：

Problem1_3,4
clear
N=input('N=');
n=0:N-1;
x3=cos(pi*n/4);
x4=sin(pi*n/4);
figure(1)
subplot(211)
stem(n,x3);%%绘制火柴梗，产生离散信号
xlabel('Time index n');
ylabel('Amplitude');
title('Original time-domain sequence x3 LEI');
subplot(212)
stem(n,x4);%%绘制火柴梗，产生离散信号
xlabel('Time index n');
ylabel('Amplitude');
title('Original time-domain sequence x4 LEI');
%DFT
X3=fft(x3,N);%%傅里叶变换
X4=fft(x4,N);%%傅里叶变换
k=0:N-1;
figure(2)
subplot(211)
stem(k,abs(X3));%%绘制火柴梗，产生离散信号
xlabel('Frequency index k');
ylabel('Amplitude');
title('Magnitude of the DFT samples X3 LEI');
subplot(212)
stem(k,abs(X4));%%绘制火柴梗，产生离散信号
xlabel('Frequency index k');
ylabel('Amplitude');
title('Magnitude of the DFT samples X4 LEI');

运行结果1_3,4：

Matlab程序3：

Problem3
clear
N=input('N=');
n=0:N-1;
k=0:N-1;
x3=cos(pi*n/4);
x4=sin(pi*n/4);
x=x3+x4;
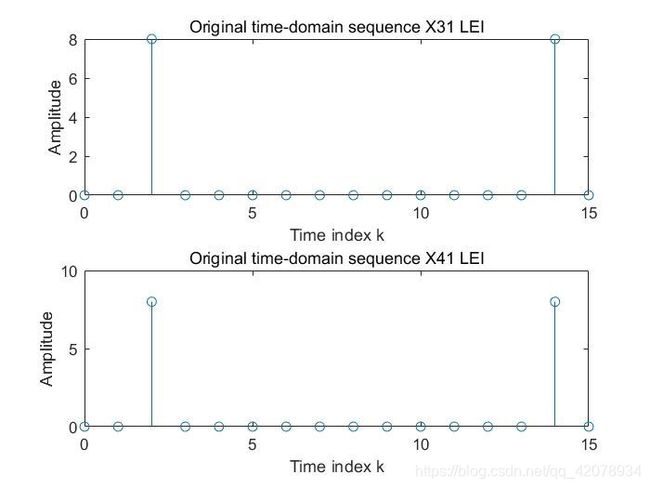
X=fft(x,N);%%傅里叶变换
X31=real(X);%%复数的实部
X41=imag(X);%%复数的虚部
figure(1)
subplot(211)
stem(k,abs(X31));%%绘制火柴梗，产生离散信号
xlabel('Time index k');
ylabel('Amplitude');
title('Original time-domain sequence X31 LEI');
subplot(212)
stem(k,abs(X41));%%绘制火柴梗，产生离散信号
xlabel('Time index k');
ylabel('Amplitude');
title('Original time-domain sequence X41 LEI');

运行结果3：

Matlab程序4：

Problem4
clear
N=input('N=');
n=0:N-1;
k=0:N-1;
x3=cos(pi*n/4);
x4=sin(pi*n/4);
xa=x3+i*x4;
xb=x3-i*x4;
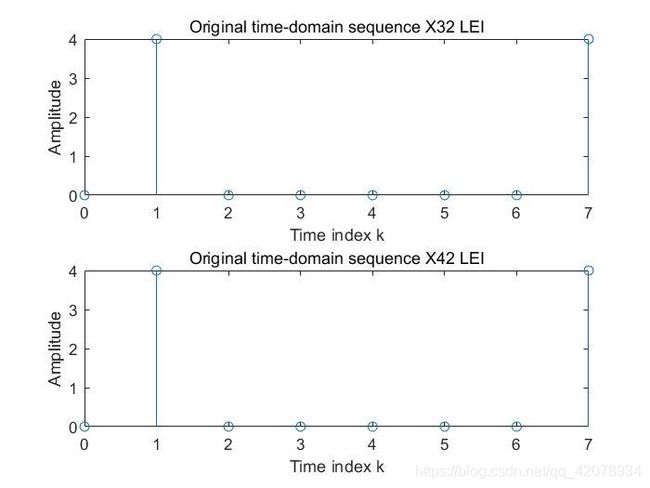
Xa=fft(xa,N);%%傅里叶变换
Xb=fft(xb,N);%%傅里叶变换
X32=0.5*(Xa+Xb);
X42=0.5*(Xa-Xb);
figure(1)
subplot(211)
stem(k,abs(X32));%%绘制火柴梗，产生离散信号
xlabel('Time index k');
ylabel('Amplitude');
title('Original time-domain sequence X32 LEI');
subplot(212)
stem(k,abs(X42));%%绘制火柴梗，产生离散信号
xlabel('Time index k');
ylabel('Amplitude');
title('Original time-domain sequence X42 LEI');

运行结果4：

Matlab程序5_a,c：

Problem5_ac
clear
k=256;
num=[0.9 -0.45 0.35 0.002];
den=[1 0.71 -0.46 -0.62];
w=0:pi/(k-1):pi;
h=freqz(num,den,w);%%计算频率响应
figure(1)
subplot(211)
plot(w/pi,abs(h));%%幅频特性曲线
title('f(t)的幅频特性曲线 LEI');
xlabel('w');
ylabel('幅度');
subplot(212)
plot(w/pi,angle(h));%%相频特性曲线
title('f(t)的相频曲线 LEI');
xlabel('w');
ylabel('相位(弧度)');
figure(2)
[z,p,k]=tf2zp(num,den);%%求得有理分式形式的系统转移函数的零、极点
zplane(num,den);%%绘制零极点
title('零极点图 LEI');

运行结果5_a,c：

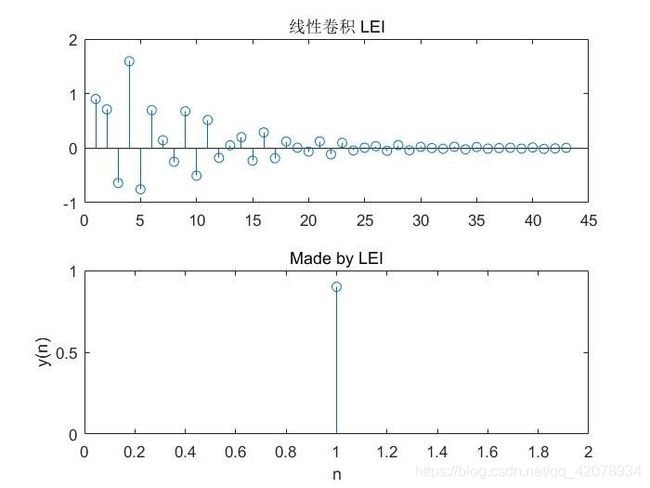
Matlab程序5_b：

Problem5_b
clear
n=40;
k=0:1:n-1;
num=[0.9 -0.45 0.35 0.002];
den=[1 0.71 -0.46 -0.62];
y1=impz(num,den,n);%%系统冲激响应
x1=[1 2 0 -0.5];
y=conv(y1,x1);%%计算卷积
subplot(211)
stem(y)
title('线性卷积 LEI');
l=length(x1)+length(y1)-1;
X=fft(x1,1);%%傅里叶变换
H=fft(y1',1);
Y=X.*H;
yy=real(ifft(Y,1));%%FFT逆变换
subplot(212)
stem(yy)
xlabel('n');
ylabel('y(n)');
title('Made by LEI');

运行结果5_b：

本人能力有限，解释尚不清楚明了，如遇任何问题，大家可留言或私信。后续将程序文件打包上传，供大家学习使用。

本文希望对大家有帮助，当然上文若有不妥之处，欢迎指正。

分享决定高度，学习拉开差距