数据结构之堆（C语言）
堆的概念和结构
堆是一种特殊的完全二叉树，堆在存储结构上是一个数组，而在逻辑结构上是一棵二叉树。其特点是每一个节点与其子节点都有着大小关系，通过这种关系我们可以把堆分为两类
- 大堆：所有的子节点的值都小于父节点，即根节点为最大值
- 小堆：所有的子节点的值都大于父节点，即根节点为最小值
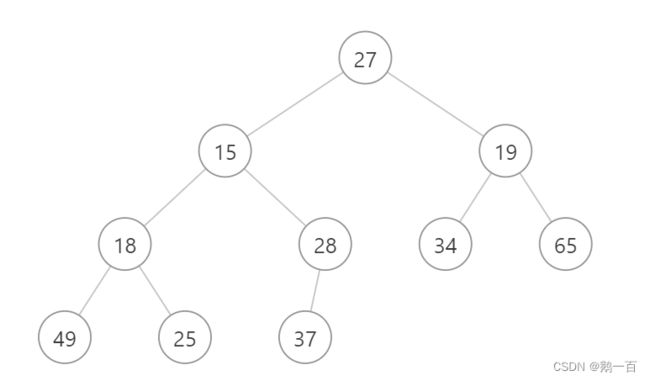
大堆示例图 
小堆示例图
大堆存储结构图 
小队存储结构图
我们发现，表示堆的数组并不是有序的，但是其有着一个大致有序的趋势。
堆的实现
1.堆的向下调整算法
向下调整算法有一个前提：其左右子树也应是一个堆。
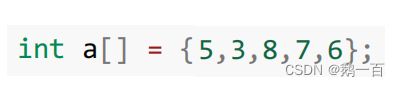
例如数组：
我们将其用二叉树的形式表现：
我们发现，其左子树是一个小堆，右子树也是一个小堆，而唯有根节点不是一个小堆。所以我们想将这个数组变成一个小堆，我们可以通过向下调整算法来改变根节点的位置，使其变成一个小堆。
步骤：
- 找到左子树和右子树中最小的值，并记录在新变量min里
- 比较父节点和min的大小，如果min大于父节点，则该堆已经是一个小堆，程序结束。如果min小于父节点，则交换min和父节点的值，然后父节点变为min节点
- 重复以上步骤，直到min节点大于父节点，或者父节点没有孩子节点（即父节点到了最后一层）
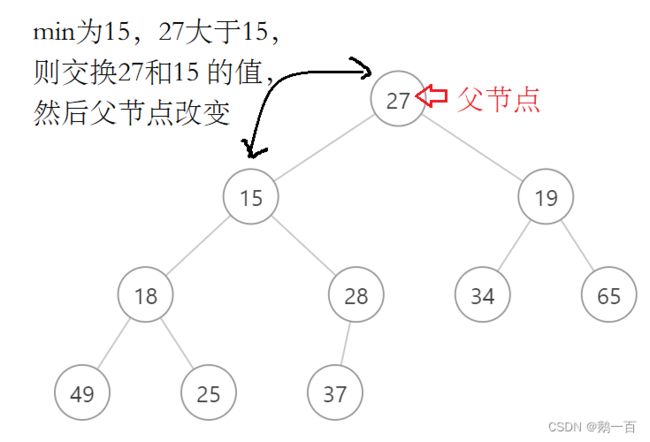第一次比较 
第二次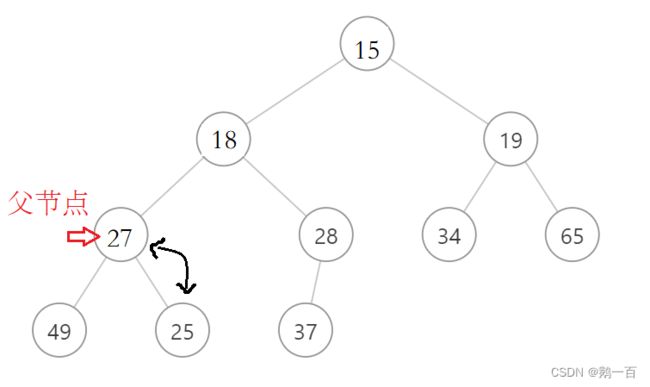比较 
第三次比较 
算法终止
通过以上操作，我们便完成了向下调整算法。
代码实现：
//堆的调整（向下调整）
typedef struct Heap
{
HPDataType* a;
int size;
int capacity;
}Heap;//堆的定义->顺序表
void downHeap(Heap* hp,int n)//hp为堆的地址，n为向下调整的元素地址
{
assert(n < hp->size);
int parent = n;
int child1 = parent * 2 + 1;
int child2 = parent * 2 + 2;
while (child2size)//如果child2大于堆的元素个数，即父节点到了最后一层，算法终止
{
int min = child1;
if (hp->a[child1] > hp->a[child2])
min = child2;
if (hp->a[parent] > hp->a[min])
{
swap(&hp->a[parent], &hp->a[min]);
parent = min;
child1 = parent * 2 + 1;
child2 = parent * 2 + 2;
}
else
{
break;
}
}
if (child2 == hp->size&& hp->a[parent] > hp->a[child1])
{
swap(&hp->a[parent], &hp->a[child1]);
}
} 2.堆的向上调整算法
有向下调整算法，自然也有向上调整算法。向下调整算法是当根节点不满足堆条件的时候使用，而如果是叶子节点不满足堆的条件，我们自然会想到从叶子节点开始向上调整。
向上调整算法的前提是该节点上层节点满足堆条件
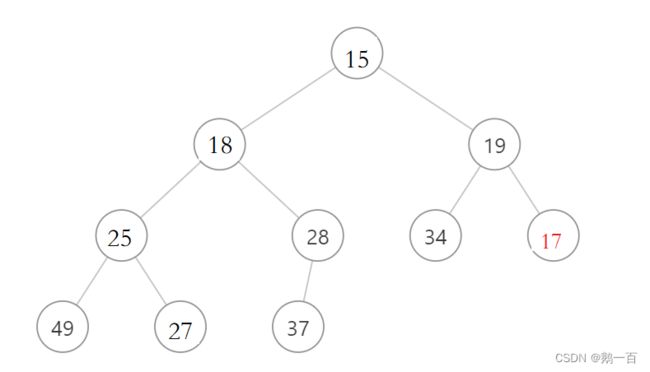
例如二叉树：
我们显然发现，17这个元素不满足小堆的条件，我们操作步骤如下
- 比较子节点和父节点的大小，如果子节点小于父节点，则交换两节点的元素，然后子节点变为交换后的节点，如果子节点大于父节点，则算法终止
- 如果子节点的地址为0，即子节点没有父节点，子节点为根节点，则算法终止
第一次比较
算法终止
代码实现：
//堆的调整（向上调整）
void upHeap(Heap* hp, int n)
{
assert(!HeapEmpty(hp));
assert(n < hp->size);
int child = n;
while (child)
{
int parent = (child - 1) / 2;
if (hp->a[child] < hp->a[parent])
{
swap(&hp->a[child], &hp->a[parent]);
child = parent;
}
else
{
break;
}
}
}3.堆的创建
假如我们需要创建堆的数组是任意一个数组，其根节点左右子树都为随意排列，我们应该如果操作呢？
假设这样一个数组：
其二叉树形式：
我们发现，这是一个小堆。如果我们想将其变成一个大堆，采用向下调整算法调整根节点，需要左右子树都是一个大堆，这显然不满足条件。
而如果采用向上调整算法调整叶子节点，需要叶子节点的上层节点都是一个大堆，这显然也不满足条件。
所以，我们可以换一种思路。我们只看叶子节点，我们会发现叶子节点往下组成的树（即只含叶子节点的树）既是一个大堆也是一个小堆，故叶子节点的父节点可以满足向下调整算法的条件。
而我们去看根节点，我们会发现只包含根节点的树既是一个大堆也是一个小堆，故根节点的子节点可以满足向上调整算法的条件。
所以综上，我们可以有两条思路：
- 从根节点开始，不断进行向上调整算法，一直到整个数组所有元素都进行向上调整
- 从最后一个叶子节点开始，不断进行向下调整算法，一直到整个数组所以元素都进行向下调整
那么既然有两种思路，哪一种思路更好呢？
先说结论：第二种思路（向下调整算法）更好。
原因：
对于同一个数组，我们都以最差的情况来考虑（即从小堆调整为大堆）
如果我们采取向下调整算法，最后一层的元素只需调整一次，第一层的节点调整n次，如图
向下调整算法
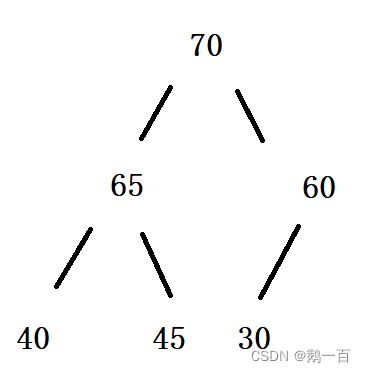
如果我们采取向上调整算法，第一层的元素调整1次，最后一层的元素调整n次，如图
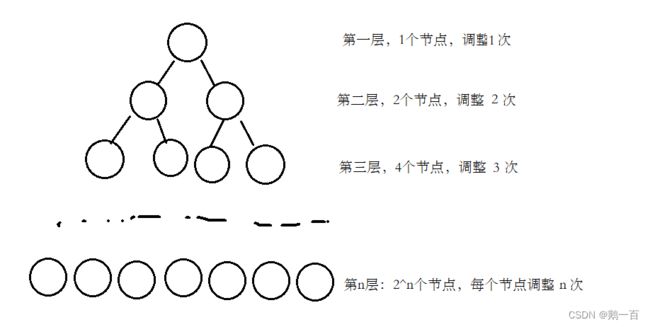向上调整算法
我们不需要经过精确的计算，仅仅目测比较便可以发现，两种算法相比，向上调整算法用最多的元素乘以了最大的次数，而向下调整算法相反，以最多的元素乘以最小的次数，自然向下调整算法的效率更高。
而经过计算我们可以直到，两种算法分别的时间复杂度：
故建堆我们采用向下调整算法。
代码实现：
//向下调整
void AdjustDown(int* a, int num, int root)
{
int child1 = root * 2 + 1;
int child2 = root * 2 + 2;
while (child1 < num)
{
int max = child1;
if (child2 a[root])
Swap(&(a[max]), &(a[root]));
root = max;
child1 = root * 2 + 1;
child2 = root * 2 + 2;
}
}
void CreateHeap(int* a,int num)
{
int end = (num - 1) / 2;
//将数组变为堆
while (end >= 0)
{
AdjustDown(a, num, end);
end--;
}
} 4. 堆的插入
我们只需要将数据插入到数组的最后一个位置，然后将插入的数组向上调整即可。
代码实现：
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
assert(hp);
if (hp->size == hp->capacity)
{
HPDataType* tmp = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * (hp->capacity) * 2);
hp->capacity *= 2;
hp->a = tmp;
}
hp->a[hp->size] = x;
hp->size++;
upHeap(hp, hp->size-1);
}
5.堆的删除
对于堆的删除，我们可不可以像顺序表的删除一样，删去首元素，然后将后面元素往前挪一格便可？
我们来进行测试，我们有这样一个堆：
其二叉树形式：
如果我们删去了第一个元素1，那剩下的堆为：
其二叉树形式为：
我们发现，这已经不再是一个小堆了。
所以，如果直接将首元素进行删除，则会改变堆的结构，我们必须找到一个不会改变堆的结构的方法来对元素进行删除。
此时，我们可以交换首元素和尾元素，交换之后我们发现堆的其余元素结构并没有改变，我们删去最后一个元素并不会对堆的其他元素产生影响，然后我们再通过向下调整算法调整交换到跟接待你的尾元素，我们仅仅对一个元素进行操作便使这棵树重新恢复成了堆。
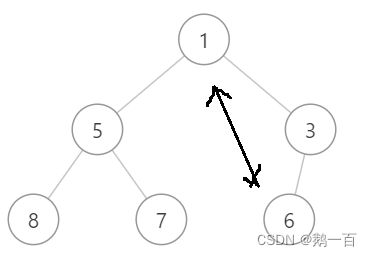交换首尾元素 
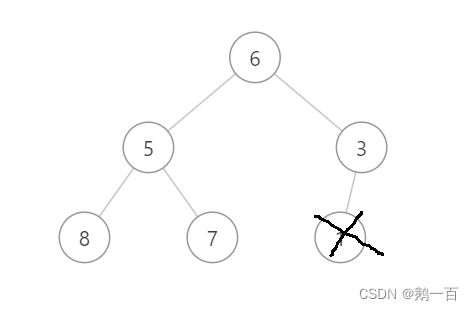删去元素 
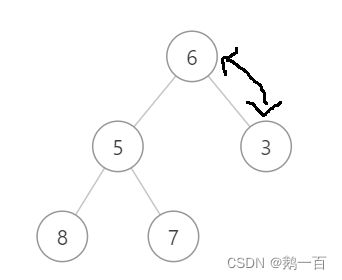向下调整
代码实现：
// 堆的删除
void HeapPop(Heap* hp)
{
assert(!HeapEmpty(hp));
swap(&hp->a[0], &hp->a[hp->size - 1]);
hp->size--;
if (hp->size > 0)
downHeap(hp, 0);
}