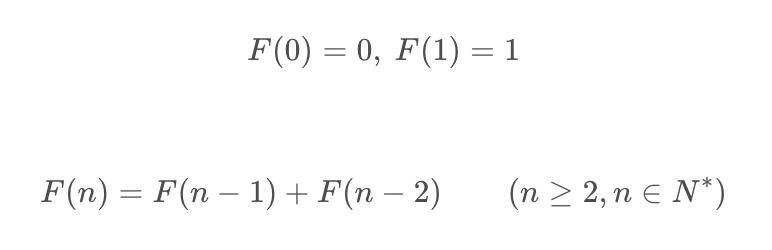数据结构与算法——静态查找&动态查找
今天在学习的时候不懂静态查找和动态查找的区别,通过查询资料,于是有了以下内容。
一、静态查找
静态查找指的是只对表执行查找操作,并不会动态添加元素。静态查找主要有顺序查找和二分查找两大类,接下来我们依次讲解一下。
1,顺序查找
顺序查找指的是线性表中的元素查找,按照元素是否有序,可以分为【无序线性表的顺序查找】和【有序线性表的顺序查找】。接下来我所要介绍的两种算法都是针对的是无序线性表的顺序查找。
(1)原始算法
对于一般的无序线性表,其顺序查找的思想如下:
从线性表的一端开始,逐个检查关键字是否满足条件。若查到某个元素的关键字满足给定条件,则查找成功,并返回该元素在线性表中的位置;若已经找到线性表的另一端了,但是还是没有查找到符合给定条件的元素,则返回查找失败的信息。
代码如下:
/*
array是待搜索的数组
arrayCount是数组中元素个数
searchKey是搜索字段
返回值是匹配到的array中的元素的下标,这里使用-1来表示没有匹配到值
*/
int sequentialSearch(int *array, int arrayCount, int searchKey) {
for (int i = 0; i < arrayCount; i++) {
if (array[i] == searchKey) {
return i;
}
}
return -1;
}(2)优化算法——哨兵顺序查找
在上面的顺序查找原始算法中,我们可以看到,每一层遍历实际上都有俩判断:数组越界的判断、条件匹配的判断。接下来,我们通过设置一个哨兵位来减少判断,进而提高程序效率。
具体的做法如下:
在待搜索的数组中设置一个哨兵位,一般设置第0位为哨兵位,并将该哨兵位的值设置为搜索条件值。
然后从数组的最后一个位置开始循环遍历,遍历之前需要新建一个变量来记录当前循环遍历到的位置下标index,循环继续的条件是没有找到指定的元素,在每一次循环遍历体中都令index减1。
这里并不需要进行数组越界的判断,因为在0号哨兵位肯定能够匹配得到,循环也就一定能够跳出。
代码如下:
/*
array是待搜索的数组,这个数组中的0号位是哨兵位
arrayCount是数组中除了哨兵位之外的元素的个数
searchKey是搜索字段
返回值是匹配到的array中的元素的下标,这里使用哨兵位来表示没有匹配到值
*/
int sentrySequentialSearch(int *array, int arrayCount, int searchKey) {
array[0] = searchKey; // 将搜索字段设置为哨兵的值
// 从数组的最后一个元素进行倒序遍历
int index = arrayCount;
while (array[index] != searchKey) {
index--;
}
return index;
}
上面我们介绍了顺序查找以及哨兵顺序查找,他们都是针对的无序线性表,线性表中的元素是随机分布的。现在我们可以考虑一下,线性表中的元素被搜索的概率是一样的吗?肯定不是的吧。那么既然一个线性表中的各个元素被搜索的概率是不一样的,我如果事先按照搜索频率对表中的元素进行排序,那么在遍历查找的前期就更有可能找到,这样将会大大提高搜索的效率。
(3)有序线性表的顺序查找
我前面说的都是针对无序线性表,那么如果是有序线性表的话,其实还可以在上边的算法基础上进一步进行优化。
如果在查找之前就已经知道了表中的数据是有序的,那么其实就不必非得在比较到表的另外一端的时候才能确定查找失败,而是在中间就可以判断出来(下面会做详细解释),进而减少线性表查找失败的平均查找长度。
如果表L是按照关键字从小到大排列的顺序表,现在从前往后查找关键字key,当查找到第i个元素的时候,发现第i个元素对应的关键字小于key,而第i+1个元素对应的关键字大于key,此时就可以返回查找失败的信息了,而不再需要继续往前查找了,因为第i个元素之后的关键字均大于key,所以表中是不存在关键字key的元素的。
2,折半查找/二分查找
在前面介绍的顺序查找算法章节的最后,我介绍了有序线性表的顺序查找,可以减少查找失败的平均查找长度。即便如此,其实在有序顺序表中查找也是不会采取该方案的。接下来我继续来介绍一种更为高效的有序顺序表的搜索方案——二分查找法。
(1)原始算法
基本思路如下:
先找到有序顺序表中的中间元素middle,然后将其与搜索字段searchKey进行比较,这样就可以初步判断搜索的范围。既然搜索范围已经确定了,那么该搜索范围以外的其他元素就都可以不用再继续查找了(这样相较于顺序查找就可以省略一半的元素不用查找了,这就是效率啊!!!!)。然后按照前述步骤反复搜寻。
因为二分查找每一次查找都可以缩减一半的查找范围,因此二分查找的时间复杂度是O(log2(N)),而顺序查找的时间复杂度是O(log(N))。举个例子,比如某顺序表中一共有2^32个元素,那么采用二分查找法的话,最差的情况是查找32次就可以找到对应元素;但是如果是采用顺序查找法,最坏的情况是要查找2^32=4294967296次!!!可见,二分查找法的效率是非常高的~
一定要注意哦,二分查找的前提是:顺序表必须是有序的!
代码解析
① 构建一个有序顺序表,这里使用数组array
② 找到顺序表中的中间元素下标middleIndex,那么如何来找到这个中间元素呢?思路如下:通过对数组元素下标的计算来求得中间元素(中间元素下表middleIndex = (数组中最小边界下标lowIndex + 最大边界下标highIndex) / 2)
③ 取出中间元素array[middleIndex],将其与搜索字段searchKey进行比较。如果array[middleIndex] > searchKey,那么说明待搜索元素searchKey是在中间元素的左侧(假设左小右大),此时就可以调整最大边界下标highIndex为(middleIndex - 1);如果array[middleIndex] < searchKey,那么说明待搜索元素searchKey是在中间元素的右侧(假设左小右大),此时就可以调整最小边界下标lowIndex为(middleIndex + 1);如果array[middleIndex] == searchKey,那么就直接返回middleIndex。
④ 然后就是重复执行如下操作:找到中间元素array[middleIndex],比较array[middleIndex]和搜索字段searchKey的大小,然后更新searchKey新的范围,直到array[middleIndex] == searchKey(即找到searchKey)为止。那么要重复执行,就势必会使用到循环,那么循环结束的条件是什么呢?实际上,在上述循环执行过程中,lowIndex和highIndex会越来越靠近,甚至会指向同一处,在这个过程中,lowIndex会始终在highIndex的左边(即lowIndex < highIndex)。如果一直找不到指定的元素的话,俩下标必然会相互交错,即lowIndex > highIndex,此时循环结束。所以循环结束的条件就是lowIndex > highIndex。
代码如下:
/*
二分查找的前提是:数组array中的元素是有序的,本例中假设其递增。
*/
int binarySearch(int *array, int arrayCount, int searchKey) {
int lowIndex = 0;
int highIndex = arrayCount - 1;
int middleIndex;
while (lowIndex < highIndex) {
middleIndex = (lowIndex + highIndex) / 2;
if (searchKey < array[middleIndex]) {
highIndex = middleIndex - 1;
} else if (searchKey > array[middleIndex]) {
lowIndex = middleIndex + 1;
} else {
return middleIndex;
}
}
// 没有找到的话就返回-1
return -1;
}
(2)优化算法——插值查找
在上面的二分查找中,中间元素是这样确定的:
middleIndex = (lowIndex + highIndex) / 2;实际上,上述代码也可以变化一种方式,如下:
middleIndex = lowIndex + (highIndex - lowIndex) / 2;可以看到,这里取的就是1/2的位置。
如果有序线性表的数据量比较大,并且数据的分布比较均匀,那么其实这里的1/2数值的取值是可以优化的。我们可以将这里的1/2改为自适应,那么根据什么自适应呢?我们可以根据待查找元素在有序线性表中的所处位置来确定这个比例值,使得中间元素值array[middleIndex]的变化能够更靠近待查找元素searchKey,进而间接减少比较的次数。也就是说,我们是通过如下代码来确定中间元素的下标:
middleIndex = lowIndex + ((searchKey - array[lowIndex]) / (array[highIndex] - array[lowIndex])) * (highIndex - lowIndex);代码如下:
/*
插值查找
*/
int intepolationSearch(int *array, int arrayCount, int searchKey) {
int lowIndex = 0;
int highIndex = arrayCount - 1;
int middleIndex;
while (lowIndex < highIndex) {
middleIndex = lowIndex + ((searchKey - array[lowIndex]) / (array[highIndex] - array[lowIndex])) * (highIndex - lowIndex);
if (searchKey > array[middleIndex]) {
lowIndex = middleIndex + 1;
} else if (searchKey < array[middleIndex]) {
highIndex = middleIndex - 1;
} else {
return middleIndex;
}
}
return -1;
} 一定要注意哦,只有当查找有序线性表中的元素,并且线性表中的元素分布比较均匀的时候,插值排序才会比二分排序效率高;如果有序线性表的元素分配是不均匀的,那么插值排序的效率是不一定会比二分排序效率高的。
(3)斐波那契查找
上面的差值搜索,是对元素均匀分布的有序线性表的二分查找的优化;那么,如果在有序线性表中,元素的分布是不均匀的,那么如何对其二分查找进行优化呢?答案是使用斐波那契黄金分割比例。我在《数据结构与算法(六)——栈结构》中简单介绍过斐波那契数列的求解,这里只是简单介绍下斐波那契的定义,具体求解不再赘述:
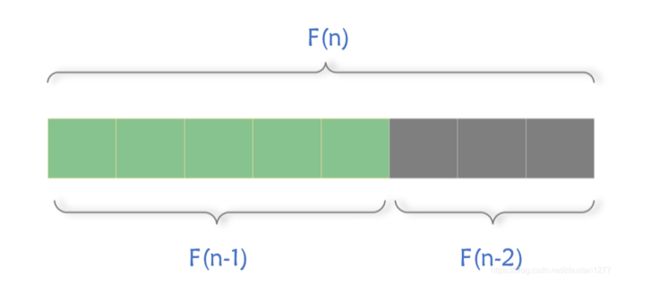
简而言之,斐波那契数列的特点就是:从第三项开始,每一项都等于它前面两项之和。我们既然知道了这个特点,那么就可以利用这个特点来做区间分割:将一个长度为F(n)的数组分为左右两段,左边一段长度是F(n-1),右边一段长度是F(n-2),如下图所示:
斐波那契搜索算法与二分查找、插值查找的基本思路是一致的,其中最重要的区别就是中间值的确定,斐波那契查找算法的中间值的计算方式如下:
middleIndex = lowIndex + F(n-1) - 1斐波那契查找算法的基本思想如下:
首先,在斐波那契数列中找到第一个大于等于有序线性表中元素个数的数F(n)。
然后将原有序线性表的长度拓展为F(n),如果需要补充元素的话,则将下标arrayCount及其之后的所有元素都补充为array[arrayCount-1],一直到新数组的长度为F(n)为止。
对原来的有序线性表拓展完成之后,就进行斐波那契分割,也就是说,将F(n)个元素分割成前半部分F(n-1)个元素和后半部分F(n-2)个元素。
随后我们找出所要查找的元素在哪一部分,然后更改边界值。
循环上述步骤,直至找到对应元素或者所有元素循环完毕为止。
前面我介绍了斐波那契查找的基本思想,根据该基本思想,斐波那契查找的详细步骤可以分为如下几步:
① 构建一个斐波那契数列F(100)
② 找到斐波那契数列中大于等于arrayCount的第一个元素F(n)
③ 有必要的话,对原来的有序线性表array进行扩容,使其元素个数等于F(n)
④ 根据斐波那契特点对扩容后的有序线性表进行分割,确定查找的中间元素底标middleIndex = lowIndex + F(n-1) - 1。这里之所以减1,是因为数组的下标是从0开始的。
⑤ 获取到中间元素array(middleIndex),并将其与搜索值searchKey进行比较。
a. 如果array(middleIndex) > searchKey,即搜索值在中间元素的左侧,由于左区间的长度是F(n-1),所以需要更新n = n-1,并且更新highIndex = middlle - 1,然后再次执行④⑤步。
b. 如果array(middleIndex) < searchKey,即搜索值在中间元素的右侧,由于右区间的长度是F(n-2),所以需要更新n = n-2,并且更新lowIndex = middlle + 1,然后再次执行④⑤步。
c. 如果array(middleIndex) < searchKey,则说明找到了目标值,但是此时还不可以直接返回middleIndex,还需要判断该中间元素是原有序线性表中的元素还是填充元素。如果middleIndex<=arrayCount-1,则说明是原有序线性表中的元素,此时直接返回middleIndex即可;如果middleIndex>arrayCount-1,则说明是填充元素,此时返回原有序线性表中的最后一个元素的下标。
代码实现如下:
#pragma mark - 斐波那契查找
// 构建斐波那契数列
void createFibonacciSequence(int arrayCount, int *fibonacciSequence, int *n) {
fibonacciSequence[0] = 1;
fibonacciSequence[1] = 1;
*n = 1;
while (fibonacciSequence[*n] < arrayCount) {
(*n)++;
fibonacciSequence[*n] = fibonacciSequence[*n - 1] + fibonacciSequence[*n - 2];
}
}
int fibonacciSearch(int *array, int arrayCount, int searchKey) {
// 1,构建斐波那契数列,并求解出第一个大于等于数组长度的斐波那契元素
int fibonacciSequence[100]; // 斐波那契数列
int n; // n是保证【fibonacciSequence[n]>=searchKey】的最小值
createFibonacciSequence(arrayCount, fibonacciSequence, &n);
// 2,对原来的有序线性表进行扩容填充
for (int i = arrayCount; i < fibonacciSequence[n]; i++) {
array[i] = array[arrayCount-1];
}
// 3,循环遍历搜索对应元素
int lowIndex = 0;
int highIndex = fibonacciSequence[n] - 1; // 之所以减1是因为下标从0开始
int middleIndex; // 中间元素下标
while (lowIndex <= highIndex) {
middleIndex = lowIndex + fibonacciSequence[n-1] - 1;
// 比较中间元素与搜索值
if (searchKey > array[middleIndex]) {
lowIndex = middleIndex + 1;
n = n - 2;
} else if (searchKey < array[middleIndex]) {
highIndex = middleIndex - 1;
n = n - 1;
} else {
return middleIndex <= arrayCount-1 ? middleIndex : arrayCount-1;
}
}
return -1;
}
int main(int argc, const char * argv[]) {
// insert code here...
printf("Hello, World!\n");
int array[100] = {1,2,3,4,5,6,7,8,9,10};
int arrayCount = 10;
printf("斐波那契查找:%d\n", fibonacciSearch(array, arrayCount, 10));
return 0;
}二、动态查找——二叉搜索树
前面我们已经知道,静态查找指的是只对表执行查找操作,并不会动态添加元素。接下来我们来介绍动态查找,也就是说,在动态查找过程中,如果没有找到对应元素的话,那么就向查找表中插入未找到的元素,或者从查找表中删除某个指定的元素。
而动态查找的方案就是二叉搜索树,又称为二叉排序树。
二叉排序树(BST,Binary Sort Tree),它要么是一棵空树,要么是一颗具有下列性质的二叉树:
① 每个节点都有唯一的值,且每个节点的值均不相同
② 若它的左子树不为空,则它的左子树的所有节点均小于根节点的值
③ 若它的右子树不为空,则它的右子树的所有节点均大于根节点的值
④ 它的左右子树均为二叉搜索树
1,二叉搜索树的查找
二叉搜索树其实就是一个排序之后的二叉树,所以其结构跟二叉树是完全一样的,如下所示:
//
// main.c
// BinarySearchTree
//
// Created by 拉维 on 2022/5/12.
//
#include
// 操作的状态
typedef enum : int {
Success,
Error,
} Status;
// BST节点结构
typedef struct BSTNode {
int data; // 数据域
struct BSTNode *leftChild; // 左子节点
struct BSTNode *rightChild; // 右子节点
} BSTNode;
// 二叉搜索树的结构
typedef struct BSTNode * BinarySearchTree; 二叉搜索树的查找其实很简单。
① 首先,找到二叉搜索树的根节点,并使用currentNode记录
② 将根节点的值与搜索值searchKey进行比较,如果正好匹配,则返回currentNode;如果searchKey小于当前节点值,则将当前节点currentNode更新为当前节点的左子节点;如果searchKey大于当前节点值,则将当前节点currentNode更新为当前节点的右子节点。
③ 循环执行上面第②步,一直到currentNode为空或者找到对应节点为止。
④ 如果到最后也没有找到,则返回NULL。
代码如下:
// BST的查找
/*
如果找到了对应元素,则parentNode是目标节点的双亲节点;如果没有找到对应元素,则parentNode是最终查找的那个节点,此时就可以将新建节点添加为parentNode的子节点
*/
struct BSTNode * bstSearch(BinarySearchTree bstRootNode, int searchKey, BinarySearchTree *parentNode) {
BinarySearchTree currentNode = bstRootNode;
*parentNode = NULL;
while (currentNode) {
if (currentNode->data == searchKey) {
break; // 跳出循环
} else if (currentNode->data > searchKey) {
*parentNode = currentNode;
currentNode = currentNode->leftChild;
} else {
*parentNode = currentNode;
currentNode = currentNode->rightChild;
}
}
return currentNode;
}2,二叉搜索树的插入
步骤如下:
1,首先,通过BST搜索来查找对应元素。在查找的过程中将最终查找的节点通过parentNode变量记录下来,如果找到了,则parentNode记录的是目标节点的父节点;如果没有找到,则parentNode记录的是最终查找到的那个节点。
2,只有在未找到目标节点的情况之下才会执行插入操作。
(1)首先新建对应节点node,并对其数值域进行赋值,左右指针均置空
(2)如果BST是一个空树,那么将BST的根节点设置为新建的node节点
(3)将插入字段insertValue与parentNode的值域进行比较,如果insertValue
代码如下:
// BST的插入
void bstInsert(BinarySearchTree *bst, int insertValue) {
// 1,在二分搜索树中查找待插入的元素
BinarySearchTree parentNode;
BinarySearchTree toInsertNode = bstSearch(*bst, insertValue, &parentNode);
// 2,如果能够找到待插入的元素,则直接略过;如果不能找到待插入的元素,则新建节点并插入到BST中
if (!toInsertNode) {
// 2.1,新建节点
struct BSTNode *node = malloc(sizeof(BSTNode));
node->data = insertValue;
node->leftChild = node->rightChild = NULL;
// 2.2,如果原BST是空树,那么将新节点设置为BST的根节点
if (!parentNode) {
*bst = node;
return;
}
// 2.3,按照左小右大进行子节点的插入
if (parentNode->data > insertValue) {
parentNode->leftChild = node;
} else if (parentNode->data < insertValue) {
parentNode->rightChild = node;
}
}
}3,二叉搜索树的节点删除
思路如下:
1,查找对应节点,如果找不到,则报错误信息;如果找到了,则执行接下来的删除操作。
2,如果待删除的节点没有左子节点,那么就可以直接将待删除节点指向其右子节点,然后销毁原待删除节点。
3,如果待删除的节点没有右子节点,那么就可以直接将待删除节点指向其左子节点,然后销毁原待删除节点。
4,如果待删除节点的左右子节点均存在,那么此时,我们这里不采取直接删除待删除节点的方式,而是选取一个合适的节点来填充到待删除节点的位置上,该合适的节点就是中序排列下的待删除节点的前驱结点
(1)查找待删除节点的左子树中的最右侧的那一个节点,即待删除节点的前驱结点preNode,并记录该前驱节点的双亲结点parentOfPreNode
(2)将前驱结点的值填充到待删除节点的位置上
(3)如果parentOfPreNode==待删除节点,那么说明待删除节点的左子节点是没有右子树的,此时将待删除节点的左子节点(即前驱结点)的双亲结点的左子节点的指向调整为前驱结点的左子节点,然后销毁原来的前驱结点
(4)如果parentOdPreNode!=待删除节点,那么说明待删除节点的左子节点是有右子树的,并且该前驱结点是没有右子节点的,因此将前驱结点的双亲节点的右子节点指针指向调整为前驱结点的左子节点,然后销毁原来的前驱节点。
代码如下:
#pragma mark - BST的元素删除
void bstDeleteNode(BinarySearchTree *toDeleteNode) {
BinarySearchTree tempNode;
if (!(*toDeleteNode)->leftChild) {
// 1,待删除节点的左子节点为空,此时只需要将待删除节点指向其右子节点即可
tempNode = *toDeleteNode;
*toDeleteNode = (*toDeleteNode)->rightChild;
free(tempNode);
} else if (!(*toDeleteNode)->rightChild) {
// 2,待删除节点的右子节点为空,此时只需要将待删除节点指向其左子节点即可
tempNode = *toDeleteNode;
*toDeleteNode = (*toDeleteNode)->leftChild;
free(tempNode);
} else {
// 3,待删除节点的左右子节点都存在
/*
实际上,BST就是中序排序的。因此,待删除节点的左子树中的最后侧的节点就是该左子树中值最大的节点,也就是待删除节点的前驱结点;待删除节点的右子树中的最左侧的节点就是该右子树中值最小的节点,也就是待删除节点的后继节点。
如果要删除待删除节点toDeleteNode,那么其实是可以将待删除节点的前驱结点或者后继节点填充到该位置的,这里是以填充前驱结点为例进行讲解。
注意咯,这里的【待删除节点toDeleteNode】是不会真正销毁的,我们选取一个合适的节点preNode来填充到该位置,然后调整preNode的双亲节点的指向,并将preNode销毁。【待删除节点toDeleteNode】只是名义上的移除,真正销毁的是填充到待删除节点位置上的前驱结点preNode。
*/
// 3.1,找寻中序排序下的前驱结点,以及前驱结点的双亲结点
BinarySearchTree preNode = (*toDeleteNode)->leftChild;
BinarySearchTree parentOfPreNode = *toDeleteNode;
while (preNode->rightChild) {
preNode = preNode->rightChild;
parentOfPreNode = preNode;
}
// 3.2,判断前驱结点的双亲节点的双亲节点是否为待删除节点自身
tempNode = preNode;
(*toDeleteNode)->data = preNode->data; // 将前驱结点的值填充到待删除节点的位置
if (parentOfPreNode == *toDeleteNode) {
/*
3.2.1 如果待删除节点的前驱节点的双亲结点是待删除节点自身,说明待删除节点的左子节点是没有右子树的,此时将待删除节点的左子节点的值填充到待删除节点的位置,并且将待删除节点指向其左子节点的左子节点,然后删除待删除节点的左子节点即可。
*/
(*toDeleteNode)->leftChild = preNode->leftChild;
} else {
/*
3.2.2 如果待删除节点的前驱结点的双亲节点不是待删除节点自身,那么说明待删除节点的左子节点是有右子树的,并且该前驱节点没有右子节点,此时需要将前驱节点的值赋值到待删除节点中,并且将前驱结点的双亲结点的右子节点指向前驱结点的左子节点,最终销毁该前驱节点。
*/
parentOfPreNode->rightChild = preNode->leftChild;
}
free(tempNode);
}
}
void bstDelete(BinarySearchTree *bst, int toDeleteValue) {
// 递归查找待删除的节点元素,如果找到指定元素,则删除;如果没有找到指定元素,则提示删除失败
if (!*bst) {
printf("删除失败,失败原因:未找到指定元素节点\n");
return;
}
if ((*bst)->data == toDeleteValue) {
bstDeleteNode(bst);
} else if((*bst)->data > toDeleteValue) {
bstDelete(&(*bst)->leftChild, toDeleteValue);
} else {
bstDelete(&(*bst)->rightChild, toDeleteValue);
}
}复制
验证代码如下:
int main(int argc, const char * argv[]) {
// insert code here...
printf("Hello, World!\n");
int originalArray[10] = {62, 88, 58, 47, 35, 73, 51, 99, 37, 93};
BinarySearchTree binarySearchTree = NULL;
for (int i = 0; i < 10; i++) {
bstInsert(&binarySearchTree, originalArray[i]);
}
BinarySearchTree parentNode;
BinarySearchTree searchNode = bstSearch(binarySearchTree, 35, &parentNode);
if (searchNode) {
printf("搜索节点%d成功\n", searchNode->data);
} else {
printf("搜索节点失败\n");
}
bstDelete(&binarySearchTree, 74);
searchNode = bstSearch(binarySearchTree, 73, &parentNode);
if (searchNode) {
printf("搜索节点%d成功\n", searchNode->data);
} else {
printf("搜索节点失败\n");
}
return 0;
}复制
验证结果如下:
4,二叉搜索树的弊端
二叉搜索树的搜索效率是与树的深度相关的,在极端情况下,二叉搜索树会退化成一条单链,如下图所示,这种情况下的搜索效率将会大大降低。
那么这种情况下该如何进行优化呢?答案是使用平衡二叉树。