机器学习-39-GAN-06-Tips for Improving GAN(改善GAN的技巧:WGAN,WGAN-GP,EBGAN,LSGAN)
文章目录
-
- Tips for Improving GAN
-
- JS divergence is not suitable(JS divergence衡量分布的问题)
- Least Square GAN (LSGAN)
- Wasserstein GAN (WGAN): Earth Mover’s Distance
-
- earth mover's distance
- Why Earth Mover’s Distance?
- WGAN
-
- WGAN
- Lipshitz Function
- weight clipping
- improve WGAN(WGAN-GP,Gradient Penalty)
- Spectrum Norm
- GAN to WGAN(如何将GAN的算法改为WGAN的算法)
- Energy-based GAN (EBGAN)
- Outlook: Loss-sensitive GAN (LSGAN)
- Reference
Tips for Improving GAN
这篇文章要说的是对传统的GAN进行的一些优化,为了使GAN更容易训练。比如WGAN,它在原始的GAN上面做了几点改动,成功地提升了原始GAN的表现。还有WGAN-GP,EBGAN和LSGAN。
JS divergence is not suitable(JS divergence衡量分布的问题)
最原始的GAN量的是 P G P_G PG和 P d a t a P_{data} Pdata之间的JS散度:
J S ( P d a t a ∣ ∣ P G ) = 1 2 K L ( P d a t a ∣ ∣ P d a t a + P G 2 ) + 1 2 K L ( P G ∣ ∣ P d a t a + P G 2 ) JS(P_{data}||P_G) = \frac{1}{2}KL\left(P_{data}||\frac{P_{data}+P_G}{2}\right)+\frac{1}{2}KL\left(P_G||\frac{P_{data}+P_{G}}{2}\right) JS(Pdata∣∣PG)=21KL(Pdata∣∣2Pdata+PG)+21KL(PG∣∣2Pdata+PG)
但是有一个严重的问题:可能两个分布没有任何的重叠,一方面的原因是由于image在高维空间中的分布其实是低维的流形(二维平面折叠在三维空间中),高维空间中的低维流形几乎是可以忽略的;另一方面,在衡量 P G P_G PG和 P d a t a P_{data} Pdata的散度的时候,我们是从两个分布中sample得到两堆data,再去量他们之间的散度,即使计算分布有重叠,但是data之间是没有重叠的,我们完全可以视data的得到的分布没有任何交集(可以用弯曲的线划开)

由于 P G P_G PG和 P d a t a P_{data} Pdata 没有任何的重合,JS散度会有很大的问题?
只要两个分布没有重叠,不管他们是不是接近,算出来的JS散度就是Log2。。。例子如图:虽然G1比G0更接近Pdata,但是从JS散度看起来,两者是没有差别的。这样的话,train起来是有问题的;(实际上在训练的时候,我们的生成器的目标是最小化 P G P_G PG和 P d a t a P_{data} Pdata 之间的散度,然后你用判别器量出散度,但是对生成器来说 P G 0 P_{G_0} PG0和 P G 1 P_{G_1} PG1是一样的,因此生成器不会将 P G 0 P_{G_0} PG0更新为 P G 1 P_{G_1} PG1)

下面从直觉角度看:为什么只要两个分布没有重叠,散度就是log2.
我们是怎样求两个分布的散度的呢?实际上的操作是:我们有两群data,把它视为两个class,然后判别器就是一个二元分类器,然后最小化交叉熵损失;只要两堆数据没有重合,那么他们的loss就是一样的,这意味着量出来的JS散度是一样的。
在原始GAN里面,当你train的是一个二元分类器时,你会发现是比较难以train的,因为没有重叠就是一样差的。
另外一个直观的想法是:当你learn一个二元分类器的话,会给蓝色的点0分,绿色点1分;output是sigmoid函数,在接近0或1的地方特别平,我们期待的是你train一个生成器,它会带领蓝色的点顺着梯度去移动分布,但是蓝色的点几乎是不动的,因为它的附近梯度几乎是0。 过去一个方法是不要把二元分类器训练的特别好(??),太好了就梯度为0了。(下图左下角)
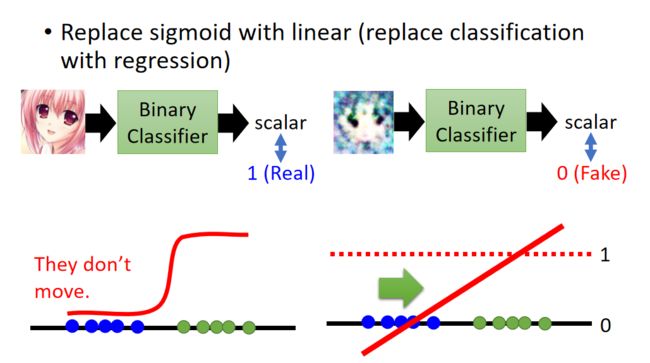
Least Square GAN (LSGAN)
看我们上图中的右下角
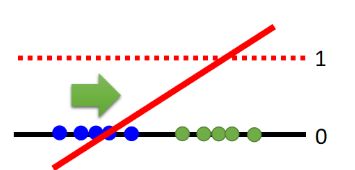
将输出的sigmiod换成linear…从分类问题,变成了回归问题。正样本越接近1越好,负样本越接近0越好。
Wasserstein GAN (WGAN): Earth Mover’s Distance
earth mover’s distance
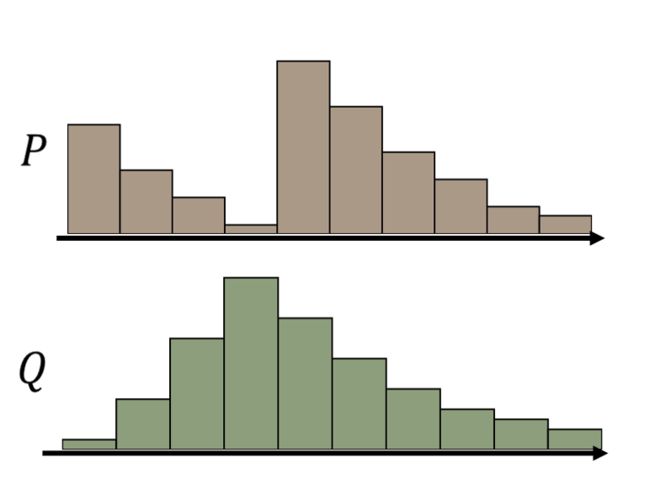
换一种方式来衡量 P G P_G PG和 P d a t a P_{data} Pdata ,用的是earth mover’s distance; 意思是假设你有两堆data P 和 Q,而你开着一个推土机,将 P土 推到 Q土 ,这个走过的距离就叫earth mover’s distance。

上面的分布是简化了的,土堆应该是这样:
出现一个问题:同样的分布,推土机可能走过的路程不一样:
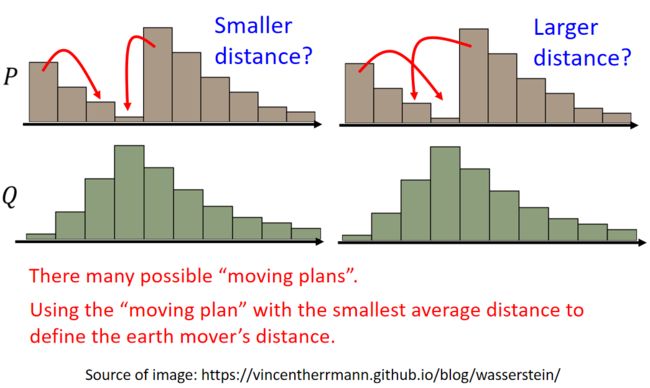
上图中的左边是是把邻近的土进行移动,右边是比较远的土进行移动。我们一般用左边的那种。
穷举所有可能的铲土的方法,每一种方法我们叫做moving plan,看哪个方法的距离最小,就是earth mover’s distance。

上图中右边是这个例子中最好的一个moving plan
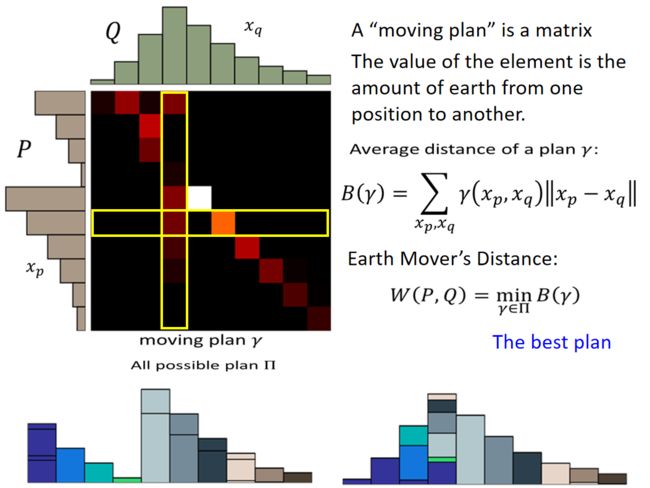
- 行x所有点加起来,对应P中对应第x堆土;
- 列y所有点加起来,对应Q中对应第y堆土。
给定矩阵(确定移动方案后) γ \gamma γ,计算移动距离 B ( γ ) B(\gamma) B(γ):
B ( γ ) = ∑ x p , x q γ ( x p , x q ) ∣ ∣ x p − x q ∣ ∣ B(\gamma) = \sum_{x_p,x_q}\gamma(x_p,x_q)||x_p-x_q|| B(γ)=xp,xq∑γ(xp,xq)∣∣xp−xq∣∣
然后穷举所有移动方案,找到最小那个就是earth mover’s distance:
W ( P , Q ) = min γ ∈ ∏ B ( γ ) W(P,Q) = \min\limits_{\gamma∈\prod}B(\gamma) W(P,Q)=γ∈∏minB(γ)
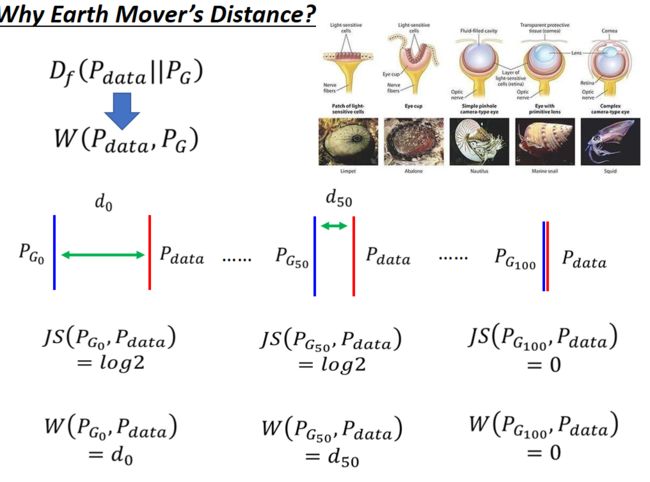
Why Earth Mover’s Distance?
我们来看:当你使用JS散度的时候,不重叠都是log2;当使用W散度的时候,当两个分布虽然不重叠但是当距离变小的时候,散度也小。
WGAN
WGAN
我们怎样改判别器,才能使判别器得到的结果是wassertein distance呢?(最大化之前的V(也就是二分类训练)得到的结果是衡量JS散度的)我们怎样改V才能使最大化V是wassertein distance呢?
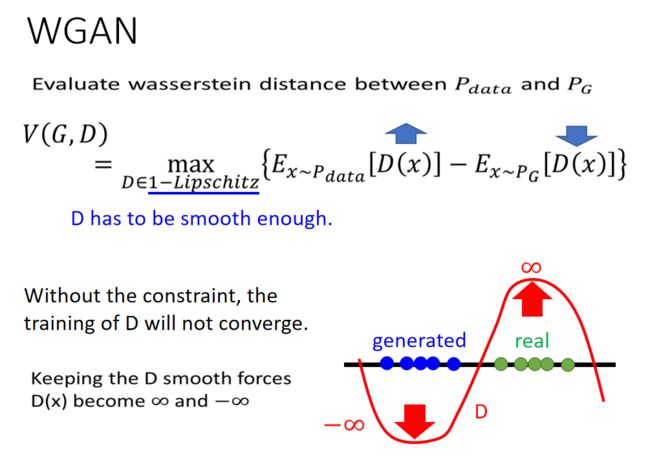
x是从 P d a t a P_{data} Pdata中sample出来的,让它的判别器输出越大越好;
x是从 P G P_{G} PG中sample出来的,让它的判别器输出越小越好;
除此之外,还要有一个约束,就是判别器必须是一个1-Lipschitz函数;一个重要特点就是它很平滑
如果没有这个约束,判别器一味着让:real的分数就越来越高,generated的分数越来越低;那么就崩溃了,永远不会收敛;因为值可以越来越大或者越来越小。看我们上图中,D就会在生成数据 P G P_{G} PG的地方趋向于负无穷大,在真实数据 P d a t a P_{data} Pdata 的地方趋向于正无穷大。两个分布就会差很多。加入平滑限制,会使得D不会无限的上升和下降,会停在某个地方。
因此必须有额外的限制,让判别器必须是平滑的
Lipshitz Function

Lipschitz Function:
∣ ∣ f ( x 1 ) − f ( x 2 ) ∣ ∣ ≤ K ∣ ∣ x 1 − x 2 ∣ ∣ ||f(x_1)-f(x_2)||≤K||x_1-x_2|| ∣∣f(x1)−f(x2)∣∣≤K∣∣x1−x2∣∣
可以看到公式左边是输出的变化,右边是输入的变化,也就是说输出的变化要小于K倍的输入的变化。
当K=1,我们就把这个满足这个不等式的函数称为1-Lipschitz
也就是:
∣ ∣ f ( x 1 ) − f ( x 2 ) ∣ ∣ ≤ ∣ ∣ x 1 − x 2 ∣ ∣ ||f(x_1)-f(x_2)||≤||x_1-x_2|| ∣∣f(x1)−f(x2)∣∣≤∣∣x1−x2∣∣
也就是不会变化很快。例如上面的绿色函数比较像1-Lipschitz Function,蓝色函数就肯定不是1-Lipschitz Function
weight clipping
如何满足1-Lipschitz Function约束条件呢?原论文使用的方法是:Weight Clipping

仍然使用梯度上升来maximize V 但是当你发现某个参数w大于你设定好的C就设定为c,小于你设定好的-C就设定为-c
还有一种方法叫做:Gradient Penalty
improve WGAN(WGAN-GP,Gradient Penalty)

对Weight Clipping进行改进,函数还是一样:
V ( G , D ) = max D ∈ 1 − L i p s c h i t z { E x ∼ P d a t a [ D ( x ) ] − E x ∼ P G [ D ( x ) ] } V(G,D) = \max\limits_{D∈1-Lipschitz}\left\{E_{x\sim P_{data}}[D(x)]-E_{x\sim P_G}[D(x)]\right\} V(G,D)=D∈1−Lipschitzmax{Ex∼Pdata[D(x)]−Ex∼PG[D(x)]}
但是Improved WGAN对于约束换了一个角度,就是梯度的norm要小于等于1。也就是说如果一个函数是1-Lipschitz的话,等价于:对于所有的input x都去求梯度的话,则梯度的norm总是小于等于1:
D ∈ 1 − L i p s c h i t z ← → ∣ ∣ ▽ x D ( x ) ∣ ∣ ≤ 1 ( f o r a l l x ) D∈1-Lipschitz \leftarrow\rightarrow ||▽_xD(x)||≤ 1 \ \ \ ( for \ all \ x) D∈1−Lipschitz←→∣∣▽xD(x)∣∣≤1 (for all x)
关于norm的计算是有一个近似计算的方法的:
V ( G , D ) ≈ max D { E x ∼ P d a t a [ D ( x ) ] − E x ∼ P G [ D ( x ) ] } − λ ∫ x max ( 0 , ∣ ∣ ▽ x D ( x ) ∣ ∣ − 1 ) d x V(G,D) ≈ \max\limits_D\{E_{x\sim P_{data}}[D(x)]-E_{x\sim P_G}[D(x)]\}\ - \ \lambda\int_x \max(0,||▽_xD(x)||-1)dx V(G,D)≈Dmax{Ex∼Pdata[D(x)]−Ex∼PG[D(x)]} − λ∫xmax(0,∣∣▽xD(x)∣∣−1)dx
后面这个积分项类似于正则项,它的作用是对所有的x做积分,然后取一个max,这个max的意思当Discriminator的梯度的norm大于1,那么就会存在正则项,如果Discriminator的梯度的norm小于1,那么这项为0,没有正则项(不惩罚)。但是这样会有问题,我们不可能对所有高维空间中的x都进行求积分这个操作,我们的x是sample出来的。因此再次把正则项进行近似:
− λ E x ∼ P p e n a l t y [ m a x ( 0 , ∣ ∣ ▽ x D ( x ) ) ∣ ∣ − 1 ) ] \ \ \ \ \ \ \ \ \ -\lambda E_{x\sim P_{penalty}}[max(0,||▽_xD(x))||-1)] −λEx∼Ppenalty[max(0,∣∣▽xD(x))∣∣−1)]
这个正则项保证所有采样出来的x满足Discriminator的梯度的norm小于1
Penalty(中文意思:惩罚)长什么样子呢?
实际上这个penalty项就是从 P d a t a P_{data} Pdata 中随便取一点,然后从 P G P_G PG 中随便取一点,然后在这两点的连线上进行采样,得到 x ∼ p e n a l t y x \sim penalty x∼penalty

把这些sample到的x ∼ p e n a l t y 范围画出来就是上面的蓝色部分,为什么不是对整个空间中的x都做penalty呢?原文说实验结果表明这样做结果比较好。。。
从另外一个方面来看, P G P_G PG要沿着梯度的方向向 P d a t a P_{data} Pdata 靠近,靠近移动的方向就是蓝色区域,其他区域也不会去,所以在它们之间的 P p e n a l t y P_{penalty} Ppenalty 这个区域会影响到最后的结果,这也是为什么WGAN优化的是 P p e n a l t y P_{penalty} Ppenalty 。不过 P p e n a l t y P_{penalty} Ppenalty 最近有新的观点说到其实应该优化 P d a t a P_{data} Pdata 的区域而不是 P p e n a l t y P_{penalty} Ppenalty 。这里说的是原始版本的WGAN

再来一个trick,之前说近似后的约束是希望梯度大于1就会有惩罚,小于1不会有惩罚,也就是 m a x ( 0 , ∣ ∣ ▽ x D ( x ) ∣ ∣ − 1 ) max(0,||▽_xD(x)||-1) max(0,∣∣▽xD(x)∣∣−1)。但是在实做的时候,用的正则项是:
( ∣ ∣ ▽ x D ( x ) ∣ ∣ − 1 ) 2 (||▽_xD(x)||-1)^2 (∣∣▽xD(x)∣∣−1)2
意思是希望梯度越接近1越好。原文:
“Simply penalizing overly large gradients also works in theory, but experimentally we found that this approach converged faster and to better optima.”
理由就是实作上效果好。。。
当然这个方法也有缺点,它的penalty的点是从两个分布中随机选点然后连接,然后做采样,如果有下图的两个分布明显这样做有问题:

选择红色那个点是不好的,(因为黄色的点移动也是移动到黑色点那个位置,也就是以黑色点为目标,而不是以红色点为目标。)应该选下图中黑色的点的连线来做采样比较合适。但是找黑色的点又比较麻烦。。。

后来又研究者对Improved WGAN提出Improved Improved WGAN算法,改进的地方在于把penalty放在了 P d a t a P_{data} Pdata的范围。
Spectrum Norm
上面讲的WGAN比较弱,一来都是用近似的方法搞的,解释不通就说反正实作就是这样;二来只有在某个区域Discriminator的norm才会满足小于1的条件。Spectrum Norm就直接,所有范围的x经过Discriminator后的norm都会满足小于1的条件。(不展开)
简单地说是对每层网络的参数除以该层的谱范数来满足Lipschitz=1的约束,该技术被称为Spectrum Norm(谱归一化)
Spectral Normalization → Keep gradient norm smaller than 1 everywhere
也就是让每一个位置的梯度范数都小于1
下面是生成狗狗的DEMO:
GAN to WGAN(如何将GAN的算法改为WGAN的算法)
我们首先看一下原始GAN 的算法:

前面提及太多次了,就不说了。看一下使用WGAN之后的算法:

WGAN: 要改四个地方:
-
改V
sigmoid拿掉变成线性
使用Weight clipping 或者 Gradient Penalty(加上正则化项)等
-
改生成器更新公式
Energy-based GAN (EBGAN)
把判别器改成了 autoencoder
对于一般的判别器,你需要让生成器慢慢变强,你的判别器才会强;但是autoencoder的判别器可以pre-train,可以用正样本进行预训练;一开始的判别器会很强,这样你的生成器一开始就会产生很好的image;

生成的图片进入粉色部分(Discriminator),先经过一个Autoencoder,还原后,计算出还原图像和原图的reconstruction error(上图中是0.1),然后乘上一个 -1,得到Discriminator的输出(上例中是-0.1)
所以从整体上来看Discriminator和之前的GAN的Discriminator一样,输入一个对象,得到这个对象和真实对象的差距,只不过是得到这个差距的方法不一样,之前是JS divergence,这里是Autoencoder。简单来说就是根据一个图片是否能够被reconstruction,如果能被还原得很好,说明这个图片是一个high quality的图片,反之亦然。
这个方法的好处就是Autoencoder是可以pretrain的,不需要negative example来训练,直接给它positive example来minimize reconstruction error即可。
Using the negative reconstruction error of auto-encoder to determine the goodness.
Benefit: The auto-encoder can be pre-train by real images without generator.
这样还有一个好处,原来的GAN刚开始训练的时候generator和discriminator都很弱,要不断迭代后discriminator才随着generator的变强而变强,这个方法discriminator不依赖generator,直接开局就很强。

EBGAN在训练的时候有一个trick,如果只是希望生成图片(蓝色)的分数,即reconstruction error越大越好(取负号后变小),那么会让autoencoder训练出来直接输出noise,因为Hard to reconstruct, easy to destroy,要得到低分很简单,只要输出noise,就会得到reconstruction error超级大(取负号后变小),这样训练出来的discriminator不是我们想要的。
因此我们会在训练的过程中为reconstruction error(取负号后)添加一个margin下限(超参数),让reconstruction error(取负号后)小到一定程度即可。
Outlook: Loss-sensitive GAN (LSGAN)
这个GAN也用到了margin的概念,之前的WGAN,Discriminator是希望真实数据得分越大越好,生成数据得分越小越好
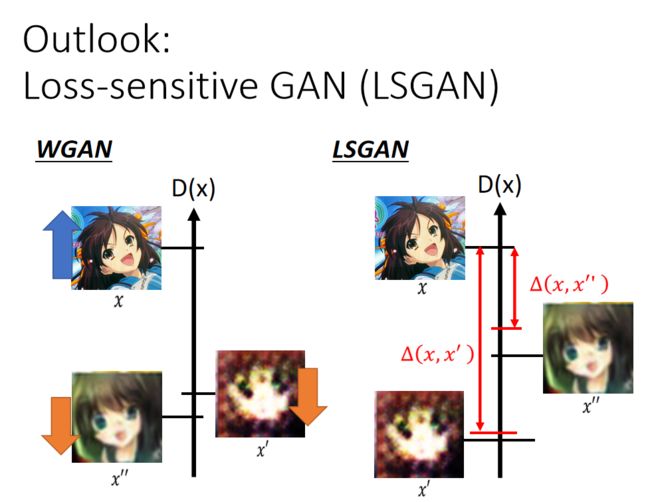
但是有些生成数据已经比较真实了,没有必要要搞得很小。例如:下图中的 x ′ ′ x'' x′′比较接近真实数据 x x x,即 Δ ( x , x ′ ′ ) \Delta(x,x'') Δ(x,x′′)比较小, x ′ x' x′没有那么接近真实数据 x x x,即 Δ ( x , x ′ ) \Delta(x,x') Δ(x,x′) 比较大,可以看到 Δ ( x , x ′ ) \Delta(x,x') Δ(x,x′)的margin压得比较小,而 Δ ( x , x ′ ′ ) \Delta(x,x'') Δ(x,x′′) 的margin比较大。
Reference
- Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, Yoshua Bengio, Generative Adversarial Networks, NIPS, 2014
- Sebastian Nowozin, Botond Cseke, Ryota Tomioka, “f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization”, NIPS, 2016
- Martin Arjovsky, Soumith Chintala, Léon Bottou, Wasserstein GAN, arXiv, 2017
- Ishaan Gulrajani, Faruk Ahmed, Martin Arjovsky, Vincent Dumoulin, Aaron Courville, Improved Training of Wasserstein GANs, NIPS, 2017
- Junbo Zhao, Michael Mathieu, Yann LeCun, Energy-based Generative Adversarial Network, arXiv, 2016
- Mario Lucic, Karol Kurach, Marcin Michalski, Sylvain Gelly, Olivier Bousquet, “Are GANs Created Equal? A Large-Scale Study”, arXiv, 2017
- Tim Salimans, Ian Goodfellow, Wojciech Zaremba, Vicki Cheung, Alec Radford, Xi Chen Improved Techniques for Training GANs, NIPS, 2016
- Martin Heusel, Hubert Ramsauer, Thomas Unterthiner, Bernhard Nessler, Sepp Hochreiter, GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium, NIPS, 2017
- Naveen Kodali, Jacob Abernethy, James Hays, Zsolt Kira, “On Convergence and Stability of GANs”, arXiv, 2017
- Xiang Wei, Boqing Gong, Zixia Liu, Wei Lu, Liqiang Wang, Improving the Improved Training of Wasserstein GANs: A Consistency Term and Its Dual Effect, ICLR, 2018
- Takeru Miyato, Toshiki Kataoka, Masanori Koyama, Yuichi Yoshida, Spectral Normalization for Generative Adversarial Networks, ICLR, 2018