基于混沌映射的自适应正余弦优化算法
文章目录
- 一、理论基础
-
- 1、正余弦优化算法
- 2、改进正余弦优化算法
-
- (1)采用Logistic混沌映射的初始解
- (2)调节因子 r 1 r_1 r1的优化及惯性权重因子
- 二、仿真实验与分析
- 三、参考文献
一、理论基础
1、正余弦优化算法
请参考这里。
2、改进正余弦优化算法
(1)采用Logistic混沌映射的初始解
本文采用Logistic混沌映射方法来改进初始化的随机解,可随机性地生成均匀且不重复的初始解集,其数学表达式描述为: x n + 1 = μ x n ( 1 − x n ) (1) x_{n+1}=\mu x_n(1-x_n)\tag{1} xn+1=μxn(1−xn)(1)其中, μ \mu μ为Logistic控制参数,且 μ ∈ ( 0 , 4 ] \mu\in(0,4] μ∈(0,4]; x n ∈ ( 0 , 1 ) x_n\in(0,1) xn∈(0,1);本文 μ \mu μ的取值为4。
(2)调节因子 r 1 r_1 r1的优化及惯性权重因子
为了平衡全局搜索和局部开发的关系,本文采用双曲正弦函数进行改进,改进后的调节因子 r 1 r_1 r1表达式为: r 1 = 1 − T 5 × sinh ( t 3 100 ⋅ T 3 ) (2) r_1=1-\frac T5×\sinh(\frac{t^3}{100\cdot T^3})\tag{2} r1=1−5T×sinh(100⋅T3t3)(2)其中, t t t表示当前迭代次数, T T T表示最大迭代次数。从式(2)可以着出,在迭代的前期,调节因 r 1 r_1 r1值相对较大且递减的变化速度较慢,能够通过较大的步长进行搜索;而到了迭代的后期,调节因子 r 1 r_1 r1值的递减变化速度加快,可使最优解快速收敛。
为了进一步提升算法的局部开发能力, 在个体更新的过程中增加了动态惯性权重因子 w w w,结合上述双曲正弦调节因子 r 1 r_1 r1的改进, 改进后的位置更新表达式为: x i D ( t + 1 ) = { w ⋅ x i D ( t ) + r 1 ⋅ sin ( r 2 ) ⋅ ∣ r 3 P D t − x i D ( t ) ∣ , r 4 < 0.5 w ⋅ x i D ( t ) + r 1 ⋅ cos ( r 2 ) ⋅ ∣ r 3 P D t − x i D ( t ) ∣ , r 4 ≥ 0.5 (3) x_{iD}(t+1)=\begin{dcases}w\cdot x_{iD}(t)+r_1\cdot\sin(r_2)\cdot|r_3P_D^t-x_{iD}(t)|,\quad r_4<0.5\\w\cdot x_{iD}(t)+r_1\cdot\cos(r_2)\cdot|r_3P_D^t-x_{iD}(t)|,\quad r_4≥0.5\end{dcases}\tag{3} xiD(t+1)={w⋅xiD(t)+r1⋅sin(r2)⋅∣r3PDt−xiD(t)∣,r4<0.5w⋅xiD(t)+r1⋅cos(r2)⋅∣r3PDt−xiD(t)∣,r4≥0.5(3)其中,惯性权重因子 w w w的表达式为: w ( t ) = w max − ( w max − w min ) ⋅ t T (4) w(t)=w_{\max}-(w_{\max}-w_{\min})\cdot\frac tT\tag{4} w(t)=wmax−(wmax−wmin)⋅Tt(4)其中, w max w_{\max} wmax和 w min w_{\min} wmin分别为惯性权重最大值和最小值。同理,通过式(4)的结构也可看出,随着迭代次数的増大, w ( t ) w(t) w(t)逐渐递减,在前期阶段有助于全局搜索,而到了迭代的后期,则更有助于局部开发,从而有效提高算法的收敛精度和速度。
由于本文在标准SCA算法基础上仅对种群初始化、调节因子和惯性权重因子做了改进,所以算法的复杂度与原标准SCA算法仍保持一致,即在未使算法变的更复杂的情况下,大幅改善了算法的性能。
二、仿真实验与分析
为了验证本文提出的IM-SCA算法性能,选择8个具有代表性的基准函数进行测试,并与标准SCA算法进行对比,基准测试函数描述如表1所示。其中,前4个是单峰函数,后4个是多峰函数。

设置维数 D = 20 D=20 D=20,种群规模 N = 30 N=30 N=30,最大迭代次数 T = 500 T=500 T=500,为了避免偶然性的干扰,保证测试的准确度,分别采用标准SCA算法以及本文提出的IM-SCA算法对表1中的8个函数独立运行25次。
结果显示如下:





函数:F1
SCA:最优值: 9.6513e-06,最差值:0.25013,平均值:0.024266,标准差:0.055197
IM-SCA:最优值: 0,最差值:0,平均值:0,标准差:0
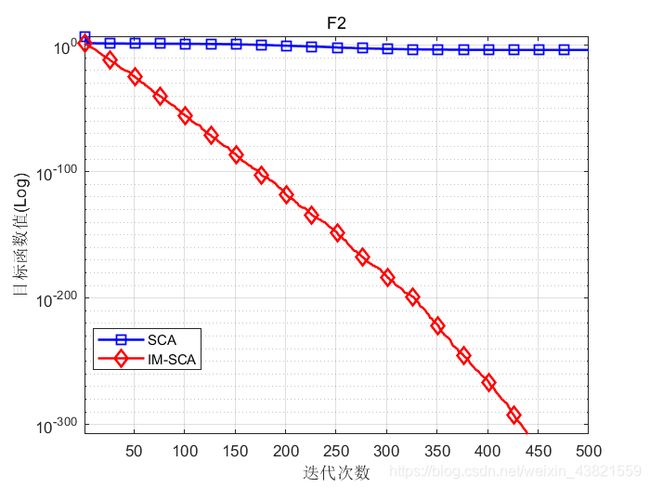
函数:F2
SCA:最优值: 2.8624e-06,最差值:0.0025485,平均值:0.00019964,标准差:0.00050354
IM-SCA:最优值: 0,最差值:0,平均值:0,标准差:0
函数:F3
SCA:最优值: 0.36068,最差值:19.9281,平均值:6.56,标准差:6.0081
IM-SCA:最优值: 0,最差值:0,平均值:0,标准差:0
函数:F4
SCA:最优值: 0.00097847,最差值:0.072605,平均值:0.015826,标准差:0.018114
IM-SCA:最优值: 1.2656e-05,最差值:0.00024853,平均值:9.4924e-05,标准差:6.4001e-05
函数:F5
SCA:最优值: -3804.4731,最差值:-2669.4781,平均值:-3117.1216,标准差:344.716
IM-SCA:最优值: -2635.493,最差值:-1696.652,平均值:-2132.9732,标准差:287.3696
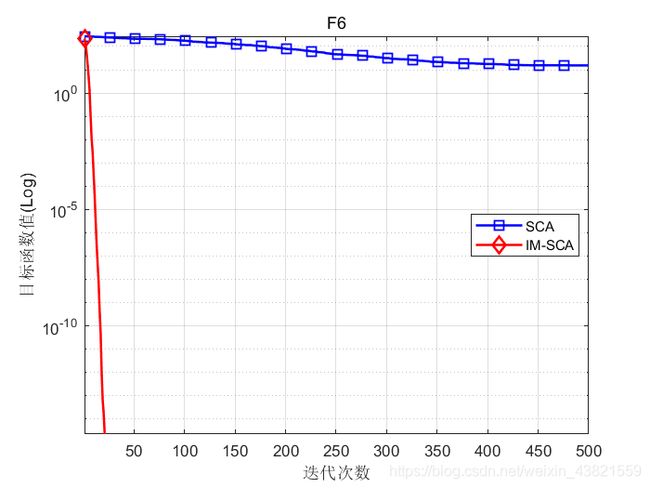
函数:F6
SCA:最优值: 0.002272,最差值:51.7738,平均值:15.3019,标准差:16.2941
IM-SCA:最优值: 0,最差值:0,平均值:0,标准差:0
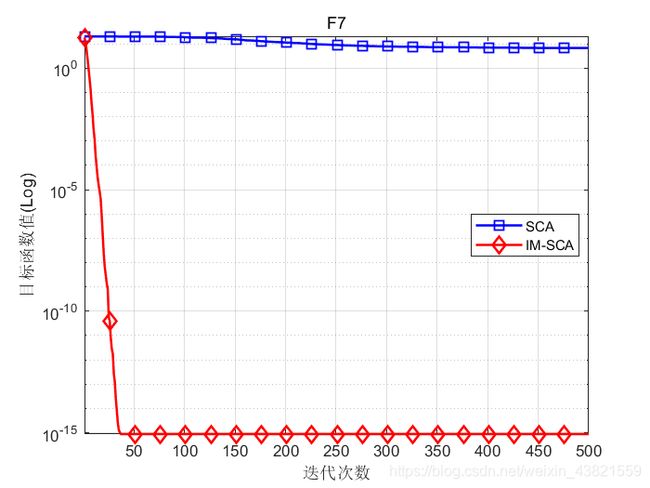
函数:F7
SCA:最优值: 0.00017779,最差值:20.2168,平均值:6.6549,标准差:9.0613
IM-SCA:最优值: 8.8818e-16,最差值:8.8818e-16,平均值:8.8818e-16,标准差:0
函数:F8
SCA:最优值: 0.00013533,最差值:0.9761,平均值:0.24568,标准差:0.22527
IM-SCA:最优值: 0,最差值:0,平均值:0,标准差:0
结果验证了本文提出的改进策略可以有效避免陷入局部最优,改善了算法的遍历性,并提高了算法的收敛精度和鲁棒性。
三、参考文献
[1] 刘丽娟, 刘定一, 刘婷婷. 改进的正余弦优化算法在WSN覆盖中的应用[J]. 数学的实践与认识, 2021, 51(11): 129-137.