bmzctf-crypto writeup（二） (持续更新)

2018 HEBTUCTF lazy cipher

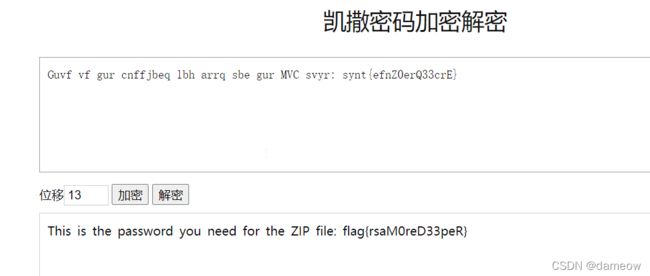
看到这样的乱乱的字母，首先要反应到用词频分析：https://quipqiup.com/

直接出flag，根本不需要知道题目考察什么。

火眼金睛

给了两个文件，是加密的。

7zip打不开，说明不是伪加密。
尝试爆破：

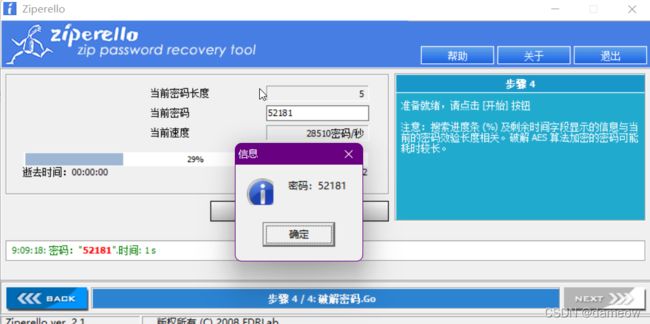
密码52181
发现里面还有一层。

外面有一个readme.txt，里面也有一个readme.txt，所有考虑明文攻击。
（但是我就是不成功，看别人的也是明文攻击啊。。。）

淦。。。

1837

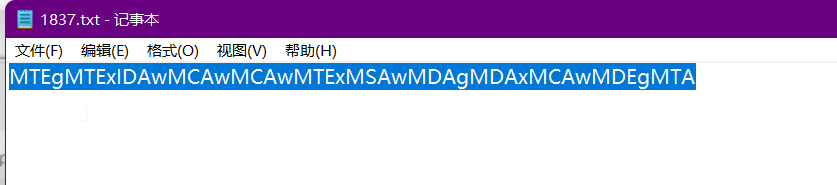
拿去base64解密，得到二进制。

把二进制转字符串，转十进制怎么都不对，没想到是摩斯电码，摩斯电码是1837发明的，对应的题目。


flag{MOSI1SFUN}

Caesar

Can you untie it?

ch\at]ZW+S$)6Q#k

Tip：flag格式为flag{xxx}

变异凯撒，编译的凯撒一般都是按顺序递增或者递减移位，查看前面四位和flag的关系，c到f移位3，h到l移位5，\到a移位5，a到g移位6，说明是递增。脚本：

a = 'ch\\at]ZW+S$)6Q#k'
b = ''
for i in range(len(a)):
    b += chr(ord(a[i])+ 3 + i)
print(b)

反斜杠需要转义。
flag{eca6_17Ea4}

rsa

从文件名可以看出，这是密文。
只有密文是不能解密rsa的。
从加密函数c = m^e (mod n)来看，除非e很小，造成低加密指数攻击，并且，m^e 爆破e脚本：

a = 4153372421328787064168548641845708183921443446990158572506114559735441950501706984118235944441928889749083563790293558028143373121367441549974248211570336802004821051820943229232421937298269855190652251294220483768084460779714162849925877879859830009443131489814222929347727735616113359695228615432020363240247474622132986939108457393618346100033147945959684443762976681454755482192433993286205527003029269574787026484389622816932835184754540312561890719407986296481186847292967270288752616

import gmpy2
for e in range(2,100):
    root = gmpy2.iroot(a,e)
    if root[1] == True:
        print(e)

结果是3，e=3。
那么解密脚本：

a = 4153372421328787064168548641845708183921443446990158572506114559735441950501706984118235944441928889749083563790293558028143373121367441549974248211570336802004821051820943229232421937298269855190652251294220483768084460779714162849925877879859830009443131489814222929347727735616113359695228615432020363240247474622132986939108457393618346100033147945959684443762976681454755482192433993286205527003029269574787026484389622816932835184754540312561890719407986296481186847292967270288752616

import gmpy2
root = gmpy2.iroot(a,3)

import libnum
print(libnum.n2s(int(root[0])))

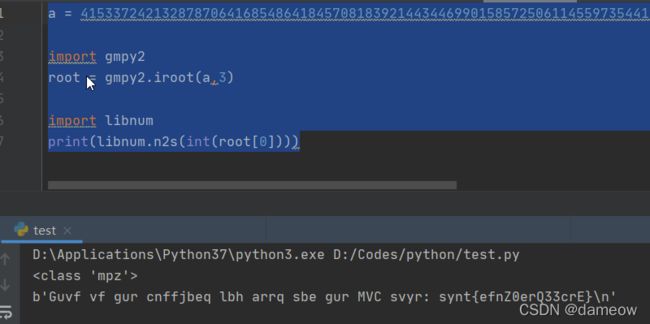
得到的synt{efnZ0erQ33crE}并不是flag，拿去词频分析，怎么都不对。

原来是凯撒密码，移位13。

技协杯-Crypto1

考察：
 RSA低加密指数攻击
 Python脚本

题目给了如下信息：
N= 27043815113145707550121063378240438939248782258483454049856453521584032220592887787562059443380038610290598575622062916485307184091409554538514854202498873547297773103239316954239641667336894313367845772845023065721439134501310426590019355844524756920078307005324929526063425487642209456355023230208467860774742785099317901398963867106582476740326082746953262216504020111095817613656347722083195076143847189035035063021757574382557663479442190050695927108198420191943271875798380684096592680930644200136436407472778630811000456073548836196890375350827356906953559602627392400524498682642018717447302297325432318177221
c=551046197285606898107283024676650283848098926639864466516013084135553632241090727641369586261735593664613285246299303875854310987447103185795040490541106154790243893699154767869461360532370258323936606948887388561062524928809730633664796872555840144662302473614722601669215346349157307079298093487429776185330734067591880338959687229983724587267427902443245768619370273994981604678382051169765413685049239926816505156737066979728449013908624429525335598674504837548523006533723449926678095026644921098893
e = 5

考虑过把模数n因数分解，但是没能分解出来。在线分解：factordb.com

考虑另外的思路，看到e很小，相对于模数n来说很小，想到低加密指数。
我们知道，RSA加密函数如下：

C = m ^e mod n 其中，c为密文，m为明文，e为加密指数，n为模数。 如果m的e次方，小于模数n，即： C = m ^e < n 那么会出现直接对密文c开e次方，便可得出明文m。 如果m的e次方，大于模数n，即： C = m ^e > n 那么必然存在一个整数k，使得： C = m ^e +kn 那么，可以爆破这个k值，同时不断地开e次方，直到能开出来。 脚本如下：

import libnum
import gmpy2

n = 27043815113145707550121063378240438939248782258483454049856453521584032220592887787562059443380038610290598575622062916485307184091409554538514854202498873547297773103239316954239641667336894313367845772845023065721439134501310426590019355844524756920078307005324929526063425487642209456355023230208467860774742785099317901398963867106582476740326082746953262216504020111095817613656347722083195076143847189035035063021757574382557663479442190050695927108198420191943271875798380684096592680930644200136436407472778630811000456073548836196890375350827356906953559602627392400524498682642018717447302297325432318177221
e = 5
flag = 0
c = 551046197285606898107283024676650283848098926639864466516013084135553632241090727641369586261735593664613285246299303875854310987447103185795040490541106154790243893699154767869461360532370258323936606948887388561062524928809730633664796872555840144662302473614722601669215346349157307079298093487429776185330734067591880338959687229983724587267427902443245768619370273994981604678382051169765413685049239926816505156737066979728449013908624429525335598674504837548523006533723449926678095026644921098893
for k in range(200000000):
    if gmpy2.iroot(c + n * k, e)[1] == 1:
        '''
        这个函数是开n次方根，gmpy2.iroot（x,n），x的n次方根。
        返回值[0]是方根，[1]是布尔值。  
        如a = gmpy2.iroot(4,2)，则返回值a[0]=2,a[1]=TRUE。
        '''
        m = gmpy2.iroot(c + n * k, e)[0]
        print(k)
        print(libnum.n2s(int(m))) # gmpy2库的数据格式是元组，元素格式是mpz，需要转成int再转string
        break

在2亿次循环中，爆破这个k值。

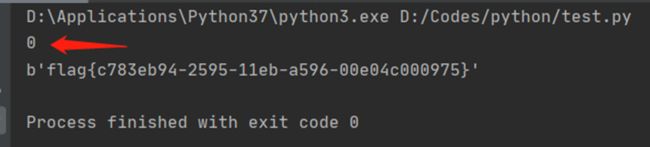
K的值是0，说明m的e次方，是小于模数n的。
flag{c783eb94-2595-11eb-a596-00e04c000975}