leetcode二叉树必刷题(1)——二叉树的前序遍历、二叉树的中序遍历、二叉树的后序遍历、二叉树的层序遍历、二叉树的层序遍历、II 二叉树的右视图、二叉树的层平均值
文章目录
- 二叉树的前序遍历
- 二叉树的中序遍历
- 二叉树的后序遍历
- 二叉树的层序遍历
- 二叉树的层序遍历 II
- 二叉树的右视图
- 二叉树的层平均值
二叉树的前序遍历
题目链接
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
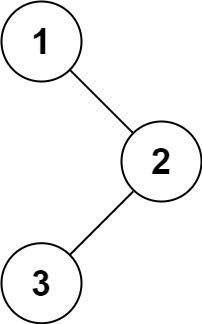
输入:root = [1,null,2,3]
输出:[1,2,3]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
示例 4:
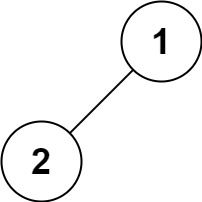
输入:root = [1,2]
输出:[1,2]
示例 5:
输入:root = [1,null,2]
输出:[1,2]
提示:
- 树中节点数目在范围
[0, 100]内 -100 <= Node.val <= 100
Python:
#递归法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
out = []
self.preOrder(root, out)
return out
def preOrder(self, node: TreeNode, nums: [int]):
if not node:
return nums
nums.append(node.val)
self.preOrder(node.left, nums)
self.preOrder(node.right, nums)
#迭代法
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
vals = list()
stack = []
node = root
while node or stack:
while node:
vals.append(node.val)
stack.append(node)
node = node.left
node = stack[-1].right
stack = stack[:-1]
return vals
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
return [root.val, *self.preorderTraversal(root.left), *self.preorderTraversal(root.right)]
#Morris 遍历
class Solution:
def preorderTraversal(self, root: TreeNode) -> List[int]:
res = list()
if not root:
return res
p1 = root
while p1:
p2 = p1.left
if p2:
while p2.right and p2.right != p1:
p2 = p2.right
if not p2.right:
res.append(p1.val)
p2.right = p1
p1 = p1.left
continue
else:
p2.right = None
else:
res.append(p1.val)
p1 = p1.right
return res
Go:
//递归法
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func preorderTraversal(root *TreeNode) (out []int) {
return preOrder(root, out)
}
func preOrder(node *TreeNode, nums []int) []int {
if node == nil {
return nums
}
nums = append(nums, node.Val)
nums = preOrder(node.Left, nums)
nums = preOrder(node.Right, nums)
return nums
}
//递归法
func preorderTraversal(root *TreeNode) (out []int) {
var preOrder func(*TreeNode)
preOrder = func(node *TreeNode) {
if node == nil {
return
}
out = append(out, node.Val)
preOrder(node.Left)
preOrder(node.Right)
}
preOrder(root)
return
}
//迭代法
func preorderTraversal(root *TreeNode) (vals []int) {
var stack []*TreeNode
for root != nil || len(stack) > 0 {
for root != nil {
vals = append(vals, root.Val)
stack = append(stack, root)
root = root.Left
}
root = stack[len(stack)-1].Right
stack = stack[:len(stack)-1]
}
return
}
//Morris 遍历
func preorderTraversal(root *TreeNode) (vals []int) {
// p1,p2定义当前节点和其左子节点
var p1, p2 *TreeNode = root, nil
// 循环遍历,直到当前节点为空
for p1 != nil {
p2 = p1.Left // 此处开始处理当前节点的左子树
if p2 != nil {
// 查找当前节点在其左子树中的前驱节点
for p2.Right != nil && p2.Right != p1 {
p2 = p2.Right
}
// 如果前驱节点的右子节点为空,则将前驱节点的右子节点设置为当前节点
if p2.Right == nil {
// 前序遍历,先访问当前节点
vals = append(vals, p1.Val)
// 将前驱节点的右子节点设置为当前节点,这样在后续遍历中可以通过此链接再次访问到当前节点
p2.Right = p1
// 访问当前节点的左子树
p1 = p1.Left
continue
}
// 如果前驱节点的右子节点不为空,则表示已经遍历完当前节点的左子树,需要断开链接
p2.Right = nil
} else {
// 如果当前节点没有左子树,则直接访问当前节点
vals = append(vals, p1.Val)
}
// 处理当前节点的右子树
p1 = p1.Right
}
return
}
二叉树的中序遍历
题目链接
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1:
输入:root = [1,null,2,3]
输出:[1,3,2]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
提示:
- 树中节点数目在范围
[0, 100]内 -100 <= Node.val <= 100
Python:
# 递归法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
out = []
def inorder(node: TreeNode):
if node:
inorder(node.left)
out.append(node.val)
inorder(node.right)
inorder(root)
return out
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
stack = []
while root or stack:
while root:
stack.append(root)
root = root.left
root = stack.pop()
res.append(root.val)
root = root.right
return res
#Morris 遍历
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
while root:
if root.left:
# 找到当前节点的左子树中的中序遍历的最后一个节点,即当前节点在中序遍历中的前驱节点
predecessor = root.left
while predecessor.right and predecessor.right != root:
predecessor = predecessor.right
if not predecessor.right:
# 如果前驱节点的右指针为空,将其指向当前节点,然后遍历左子树
predecessor.right = root
root = root.left
else:
# 如果前驱节点的右指针已经指向当前节点,说明左子树已经遍历完成,将前驱节点的右指针恢复为空
predecessor.right = None
# 将当前节点的值加入结果集
res.append(root.val)
# 遍历右子树
root = root.right
else:
# 如果没有左子树,将当前节点的值加入结果集,然后遍历右子树
res.append(root.val)
root = root.right
return res
Go:
//递归法
func inorderTraversal(root *TreeNode) (out []int) {
var inOrder func(node *TreeNode)
inOrder = func(node *TreeNode) {
if node == nil {
return
}
inOrder(node.Left)
out = append(out, node.Val)
inOrder(node.Right)
}
inOrder(root)
return
}
//迭代法
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func inorderTraversal(root *TreeNode) (res []int) {
var stack []*TreeNode
for root != nil || len(stack) > 0 {
for root != nil {
stack = append(stack, root)
root = root.Left
}
root = stack[len(stack)-1]
stack = stack[:len(stack)-1]
res = append(res, root.Val)
root = root.Right
}
return
}
//Morris 遍历
func inorderTraversal(root *TreeNode) (res []int) {
for root != nil {
if root.Left != nil {
// predecessor 节点表示当前 root 节点向左走一步,然后一直向右走至无法走为止的节点
predecessor := root.Left
for predecessor.Right != nil && predecessor.Right != root {
// 有右子树且没有设置过指向 root,则继续向右走
predecessor = predecessor.Right
}
if predecessor.Right == nil {
// 将 predecessor 的右指针指向 root,这样后面遍历完左子树 root.Left 后,就能通过这个指向回到 root
predecessor.Right = root
// 遍历左子树
root = root.Left
} else { // predecessor 的右指针已经指向了 root,则表示左子树 root.Left 已经访问完了
res = append(res, root.Val)
// 恢复原样
predecessor.Right = nil
// 遍历右子树
root = root.Right
}
} else { // 没有左子树
res = append(res, root.Val)
// 若有右子树,则遍历右子树
// 若没有右子树,则整颗左子树已遍历完,root 会通过之前设置的指向回到这颗子树的父节点
root = root.Right
}
}
return
}
二叉树的后序遍历
题目链接
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
示例 1:
输入:root = [1,null,2,3]
输出:[3,2,1]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
提示:
- 树中节点的数目在范围
[0, 100]内 -100 <= Node.val <= 100
Python:
# 递归法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
out = []
def postOrder(node):
if not node:
return
postOrder(node.left)
postOrder(node.right)
out.append(node.val)
postOrder(root)
return out
#迭代法
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
out = []
stack = []
lastVisit = None
while root or stack:
while root:
stack.append(root)
root = root.left
node = stack[-1]
if not node.right or node.right == lastVisit:
out.append(node.val)
stack.pop()
lastVisit = node
else:
root = node.right
return out
#Morris 遍历
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
def addPath(node: TreeNode):
count = 0
while node:
count += 1
res.append(node.val)
node = node.right
i, j = len(res) - count, len(res) - 1
while i < j:
res[i], res[j] = res[j], res[i]
i += 1
j -= 1
if not root:
return list()
res = list()
p1 = root
while p1:
p2 = p1.left
if p2:
while p2.right and p2.right != p1:
p2 = p2.right
if not p2.right:
p2.right = p1
p1 = p1.left
continue
else:
p2.right = None
addPath(p1.left)
p1 = p1.right
addPath(root)
return res
Go:
//递归法
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func postorderTraversal(root *TreeNode) (out []int) {
var postOrder func(*TreeNode)
postOrder = func(node *TreeNode) {
if node == nil {
return
}
postOrder(node.Left)
postOrder(node.Right)
out = append(out, node.Val)
}
postOrder(root)
return
}
//迭代法
func postorderTraversal(root *TreeNode) []int {
var stack []*TreeNode
var result []int
var prev *TreeNode // To keep track of the previously visited node
for root != nil || len(stack) > 0 {
for root != nil {
stack = append(stack, root)
root = root.Left
}
top := stack[len(stack)-1]
// Check if the right subtree is nil or already visited
if top.Right == nil || top.Right == prev {
result = append(result, top.Val)
stack = stack[:len(stack)-1]
prev = top
} else {
// Move to the right subtree
root = top.Right
}
}
return result
}
//Morris 遍历
func reverse(a []int) {
// 此函数用于反转一个切片
for i, n := 0, len(a); i < n/2; i++ {
a[i], a[n-1-i] = a[n-1-i], a[i] // 交换前后对应的元素
}
}
func postorderTraversal(root *TreeNode) (res []int) {
addPath := func(node *TreeNode) {
resSize := len(res)
for ; node != nil; node = node.Right { // 从输入的节点开始,不断向它的右子树方向遍历
res = append(res, node.Val) // 将节点的值添加到结果数组中
}
reverse(res[resSize:]) // 反转结果数组中新增的部分(详见reverse函数注释)
}
p1 := root // 从根节点开始遍历
for p1 != nil {
if p2 := p1.Left; p2 != nil { // 如果左子树存在
for p2.Right != nil && p2.Right != p1 {
p2 = p2.Right // 不断向右子树方向遍历
}
if p2.Right == nil { // 如果右子树不存在
p2.Right = p1 // 设置右子树为当前的根节点
p1 = p1.Left // 将新的根节点设置为原根节点的左子树
continue
}
p2.Right = nil // 清除右子树
addPath(p1.Left) // 对左子树进行后序遍历
}
p1 = p1.Right // 遍历右子树
}
addPath(root) // 对整个树进行后序遍历
return
}
二叉树的层序遍历
题目链接
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
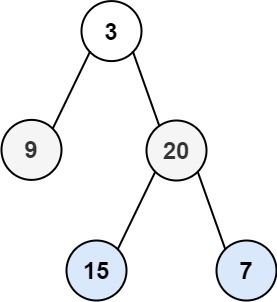
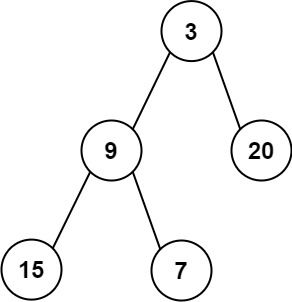
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
提示:
- 树中节点数目在范围
[0, 2000]内 -1000 <= Node.val <= 1000
Python:
# I. 按层打印: 题目要求的二叉树的 从上至下 打印(即按层打印),又称为二叉树的 广度优先搜索(BFS)。BFS 通常借助 队列 的先入先出特性来实现。
# II. 每层打印到一行: 将本层全部节点打印到一行,并将下一层全部节点加入队列,以此类推,即可分为多行打印。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if root is None:
return []
out = []
q = [root]
while q:
tmp = []
l = len(q)
for i in range(l):
node = q.pop(0)
tmp.append(node.val)
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
out.append(tmp)
return out
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
res, queue = [], collections.deque()
queue.append(root)
while queue:
tmp = []
for _ in range(len(queue)):
node = queue.popleft()
tmp.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
res.append(tmp)
return res
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if root is None:
return []
out = []
q = [root]
i = 0
while q:
p = []
out.append([])
for j in range(len(q)):
node = q[j]
out[i].append(node.val)
if node.left:
p.append(node.left)
if node.right:
p.append(node.right)
q = p
i += 1
return out
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
result = []
queue = [root]
while queue:
vals = []
next_level = []
for n in queue:
vals.append(n.val)
if n.left:
next_level.append(n.left)
if n.right:
next_level.append(n.right)
result.append(vals)
queue = next_level
return result
# 递归法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
levels = []
self.helper(root, 0, levels)
return levels
def helper(self, node, level, levels):
if not node:
return
if len(levels) == level:
levels.append([])
levels[level].append(node.val)
self.helper(node.left, level + 1, levels)
self.helper(node.right, level + 1, levels)
Go:
//自己写队列
//I. 按层打印: 题目要求的二叉树的 从上至下 打印(即按层打印),又称为二叉树的 广度优先搜索(BFS)。BFS 通常借助 队列 的先入先出特性来实现。
//II. 每层打印到一行: 将本层全部节点打印到一行,并将下一层全部节点加入队列,以此类推,即可分为多行打印。
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func levelOrder(root *TreeNode) (out [][]int) {
if root == nil {
return
}
var q []*TreeNode
q = append(q, root)
for len(q) > 0 {
var tmp []int
l := len(q)
for i := 0; i < l; i++ {
node := q[0]
tmp = append(tmp, node.Val)
q = q[1:]
if node.Left != nil {
q = append(q, node.Left)
}
if node.Right != nil {
q = append(q, node.Right)
}
}
out = append(out, tmp)
}
return
}
//使用官方包,解题思想类似
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func levelOrder(root *TreeNode) (out [][]int) {
if root == nil {
return
}
queue := list.New()
queue.PushBack(root)
for queue.Len() > 0 {
tmp := make([]int, 0)
l := queue.Len()
for i := 0; i < l; i++ {
node := queue.Remove(queue.Front()).(*TreeNode)
tmp = append(tmp, node.Val)
if node.Left != nil {
queue.PushBack(node.Left)
} else {
}
if node.Right != nil {
queue.PushBack(node.Right)
}
}
out = append(out, tmp)
}
return
}
//官方解法
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func levelOrder(root *TreeNode) [][]int {
var ret [][]int
if root == nil {
return ret
}
q := []*TreeNode{root}
for i := 0; len(q) > 0; i++ {
ret = append(ret, []int{})
var p []*TreeNode
for j := 0; j < len(q); j++ {
node := q[j]
ret[i] = append(ret[i], node.Val)
if node.Left != nil {
p = append(p, node.Left)
}
if node.Right != nil {
p = append(p, node.Right)
}
}
q = p
}
return ret
}
//递归法
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func levelOrder(root *TreeNode) [][]int {
var arr [][]int
depth := 0
var order func(root *TreeNode, depth int)
order = func(root *TreeNode, depth int) {
if root == nil {
return
}
if len(arr) == depth {
arr = append(arr, []int{})
}
arr[depth] = append(arr[depth], root.Val)
order(root.Left, depth+1)
order(root.Right, depth+1)
}
order(root, depth)
return arr
}
二叉树的层序遍历 II
题目链接
给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:[[15,7],[9,20],[3]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
提示:
- 树中节点数目在范围
[0, 2000]内 -1000 <= Node.val <= 1000
Python:
# 跟上题解法差不多,层序遍历,首部追加
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:
if root is None:
return []
out = []
q = [root]
while q:
tmp = []
l = len(q)
for i in range(l):
node = q.pop(0)
tmp.append(node.val)
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
out = [tmp] + out
return out
# 先正序再反转
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:
if root is None:
return []
out = []
q = [root]
while q:
tmp = []
l = len(q)
for i in range(l):
node = q.pop(0)
tmp.append(node.val)
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
out.append(tmp)
out.reverse()
return out
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:
if root is None:
return []
out = []
q = [root]
while q:
tmp = []
l = len(q)
for i in range(l):
node = q.pop(0)
tmp.append(node.val)
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
out.append(tmp)
return out[::-1]
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
res, queue = [], collections.deque([root])
while queue:
tmp = []
for _ in range(len(queue)):
node = queue.popleft()
tmp.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
res.append(tmp)
res.reverse()
return res
Go:
//跟上题解法差不多,层序遍历,首部追加
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func levelOrderBottom(root *TreeNode) (out [][]int) {
if root == nil {
return
}
var q []*TreeNode
q = append(q, root)
for len(q) > 0 {
var tmp []int
l := len(q)
for i := 0; i < l; i++ {
node := q[0]
tmp = append(tmp, node.Val)
q = q[1:]
if node.Left != nil {
q = append(q, node.Left)
}
if node.Right != nil {
q = append(q, node.Right)
}
}
out = append([][]int{tmp}, out...)
}
return
}
//正序输出,再反转
func levelOrderBottom(root *TreeNode) [][]int {
levelOrder := [][]int{}
if root == nil {
return levelOrder
}
queue := []*TreeNode{}
queue = append(queue, root)
for len(queue) > 0 {
level := []int{}
size := len(queue)
for i := 0; i < size; i++ {
node := queue[0]
queue = queue[1:]
level = append(level, node.Val)
if node.Left != nil {
queue = append(queue, node.Left)
}
if node.Right != nil {
queue = append(queue, node.Right)
}
}
levelOrder = append(levelOrder, level)
}
for i := 0; i < len(levelOrder) / 2; i++ {
levelOrder[i], levelOrder[len(levelOrder) - 1 - i] = levelOrder[len(levelOrder) - 1 - i], levelOrder[i]
}
return levelOrder
}
二叉树的右视图
题目链接
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:
输入: [1,2,3,null,5,null,4]
输出: [1,3,4]
示例 2:
输入: [1,null,3]
输出: [1,3]
示例 3:
输入: []
输出: []
提示:
- 二叉树的节点个数的范围是
[0,100] -100 <= Node.val <= 100
Python:
# 层序遍历的时候,判断是否遍历到单层的最后面的元素,如果是,就放进及如果数组。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
res, queue = [], collections.deque([root])
while queue:
l = len(queue)
for i in range(l):
node = queue.popleft()
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
if i == l - 1:
res.append(node.val)
return res
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
if root is None:
return []
out = []
q = [root]
while q:
l = len(q)
for i in range(l):
node = q[i]
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
if i == l - 1:
out.append(node.val)
q = q[l:]
return out
# DFS递归遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
out = []
def dfs(node: TreeNode, level: int) -> None:
if not node:
return
if level == len(out):
out.append(node.val)
dfs(node.right, level + 1)
dfs(node.left, level + 1)
dfs(root, 0)
return out
Go:
//BFS,层序遍历的时候,判断是否遍历到单层的最后面的元素,如果是,就放进及如果数组。
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func rightSideView(root *TreeNode) (out []int) {
if root == nil {
return
}
q := []*TreeNode{root}
for len(q) > 0 {
l := len(q)
for i := 0; i < l; i++ {
node := q[i]
if node.Left != nil {
q = append(q, node.Left)
}
if node.Right != nil {
q = append(q, node.Right)
}
if i == l-1 {
out = append(out, node.Val)
}
}
q = q[l:]
}
return
}
//递归法,在遍历的过程中,先访问右子树,确保右侧的节点先被处理,然后再访问左子树。这样就能保证每层最右侧的节点被加入到结果列表中。
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func rightSideView(root *TreeNode) (out []int) {
if root == nil {
return out
}
var dfs func(node *TreeNode, level int)
dfs = func(node *TreeNode, level int) {
if node == nil {
return
}
// 每层只保留最右边的节点值
if level == len(out) {
out = append(out, node.Val)
}
// 先访问右子树,确保右侧的节点先被处理
dfs(node.Right, level+1)
dfs(node.Left, level+1)
}
dfs(root, 0)
return out
}
二叉树的层平均值
题目链接
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。
示例 1:
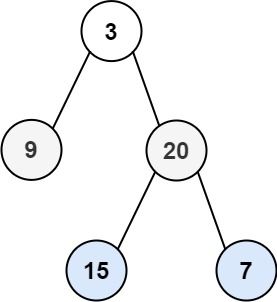
输入:root = [3,9,20,null,null,15,7]
输出:[3.00000,14.50000,11.00000]
解释:第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。
示例 2:
输入:root = [3,9,20,15,7]
输出:[3.00000,14.50000,11.00000]
提示:
- 树中节点数量在
[1, 104]范围内 -231 <= Node.val <= 231 - 1
Python:
#BFS
class Solution:
def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]:
if not root:
return []
result = []
queue = deque([root])
while queue:
level_size = len(queue)
level_sum = 0
for _ in range(level_size):
node = queue.popleft()
level_sum += node.val
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
result.append(level_sum / level_size)
return result
#DFS
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def averageOfLevels(self, root: TreeNode) -> List[float]:
def dfs(root: TreeNode, level: int):
if not root:
return
if level < len(totals):
totals[level] += root.val
counts[level] += 1
else:
totals.append(root.val)
counts.append(1)
dfs(root.left, level + 1)
dfs(root.right, level + 1)
counts = list()
totals = list()
dfs(root, 0)
return [total / count for total, count in zip(totals, counts)]
# DFS
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]:
result = []
def dfs(node, level):
if not node:
return
nonlocal result
if level < len(result):
result[level][0] += node.val
result[level][1] += 1
else:
result.append([node.val, 1])
dfs(node.left, level + 1)
dfs(node.right, level + 1)
dfs(root, 0)
return [total / count for total, count in result]
Go:
//BFS
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func averageOfLevels(root *TreeNode) (out []float64) {
if root == nil {
return
}
q := []*TreeNode{root}
for len(q) > 0 {
var tmp []int
l := len(q)
for i := 0; i < l; i++ {
node := q[i]
tmp = append(tmp, node.Val)
if node.Left != nil {
q = append(q, node.Left)
}
if node.Right != nil {
q = append(q, node.Right)
}
}
q = q[l:]
out = append(out, average(tmp))
}
return
}
func average(nums []int) float64 {
sum := nums[0]
l := len(nums)
for i := 1; i < l; i++ {
sum += nums[i]
}
return float64(sum) / float64(l)
}
//BFS
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func averageOfLevels(root *TreeNode) (out []float64) {
if root == nil {
return
}
q := []*TreeNode{root}
for len(q) > 0 {
sum := 0
l := len(q)
for i := 0; i < l; i++ {
node := q[i]
sum += node.Val
if node.Left != nil {
q = append(q, node.Left)
}
if node.Right != nil {
q = append(q, node.Right)
}
}
q = q[l:]
out = append(out, float64(sum)/float64(l))
}
return
}
//DFS
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func averageOfLevels(root *TreeNode) []float64 {
var result []float64
var dfs func(node *TreeNode, level int)
var sum []float64
var count []int
dfs = func(node *TreeNode, level int) {
if node == nil {
return
}
if level < len(sum) {
sum[level] += float64(node.Val)
count[level]++
} else {
sum = append(sum, float64(node.Val))
count = append(count, 1)
}
dfs(node.Left, level+1)
dfs(node.Right, level+1)
}
dfs(root, 0)
for i := 0; i < len(sum); i++ {
result = append(result, sum[i]/float64(count[i]))
}
return result
}
//DFS
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
type data struct{ sum, count int }
func averageOfLevels(root *TreeNode) []float64 {
var levelData []data
var dfs func(node *TreeNode, level int)
dfs = func(node *TreeNode, level int) {
if node == nil {
return
}
if level < len(levelData) {
levelData[level].sum += node.Val
levelData[level].count++
} else {
levelData = append(levelData, data{node.Val, 1})
}
dfs(node.Left, level+1)
dfs(node.Right, level+1)
}
dfs(root, 0)
averages := make([]float64, len(levelData))
for i, d := range levelData {
averages[i] = float64(d.sum) / float64(d.count)
}
return averages
}