【数据结构】第一章——绪论（4）

前言

大家好！很高兴又和大家见面啦！！！在上一篇内容中我们重点介绍了时间复杂度，今天我们要介绍的是算法的另一个目标——低存储量需求，也就是算法的空间复杂度。下面我们就来了解一下什么是空间复杂度吧！

空间复杂度

1.定义

算法的空间复杂度$S(n)$为算法所消耗的存储空间，它是问题规模$n$的函数。记为：
$$S(n)=O(g(n))$$

2.理解

我们在学习C语言时，肯定会听到这么一句话，在内存上开辟一个空间来存放数据。这里所开辟的空间也就是我们这里提到的算法所消耗的空间。
一个好算法的目标之一是需要满足低存储量需求，也就是在内存上消耗的空间越少越好，那如何分析一个算法的空间复杂度呢？

3.空间复杂度的计算

一个程序在执行时除需要存储空间来存放本身所用的指令、常数、变量和输入数据外，还需要一些对数据进行操作的工作单元和存储一些为实现计算所需信息的辅助空间。

• 若输入数据所占存储空间只取决于问题本身，和算法无关，则只需要分析输入和程序之外的额外空间。
  算法原地工作是指算法所需的辅助空间为常量，即$O(1)$。

和时间复杂度一样，空间复杂度同样也满足加法规则与乘法规则：

3.1 加法规则：

$$T(n)=T_1(n)+T_2(n)=O(f(n))+O(g(n))=O(max(f(n),g(n)))$$

3.2 乘法规则：

$$T(n)=T_1(n)\times T_2(n)=O(f(n))\times O(g(n))=O(f(n)\times g(n))$$

3.3 代码1

下面我们来看这么一个代码：

int main()
{
	int a = 10;//创建一个整型变量a，a所占空间大小为4个字节，对应的空间复杂度为O(1)
	printf("%d\n", a);//调用printf函数——int printf( const char *format [, argument]... );
	int i = 1;//创建一个整型变量i，i所占空间大小为4个字节，对应的空间复杂度为O(1)
	while (i < 100)
	{
		a += i;
		i++;
	}
	printf("%d\n", a);//调用printf函数——int printf( const char *format [, argument]... );
	return 0;
}

在这个代码中，对于main函数而言，不管是int a = 10;也好，还是int i = 1;也好，它们都是在main函数的函数栈帧内部开辟的空间，它们开辟空间的大小是固定的，一个int类型所占空间大小是4个字节，所以它们所占的空间大小为8个字节；

下面我们一起来看一下这个代码的空间消耗情况：

在这个代码中，能对空间大小产生影响的指令有：

• push——压栈指令，在函数栈顶开辟一块新的空间并存放一个元素；
• call——调用指令，在函数栈顶开辟一块新空间存放下一条指令的地址，并在这块空间上调用函数，随着函数的返回，空间会自动销毁；

通过观察，我们可以看到，除了main函数的函数栈帧的创建和printf函数的调用过程在开辟新的空间外，其它的操作都是没有对现有空间进行改变的。

变量创建的过程是通过mov指令实现的：

• mov——移动指令，将第二个操作对象的值移动得到第一个操作对象中；
• dword ptr——内存大小为4个字节的长度；
• [ebp - 8]——栈底指针向栈顶移动8字节长度的地址；
• [ebp - 14h]——栈底指针向栈顶移动20字节长度的地址；

从这些指令中可以看到，创建变量的过程，实质上就是在main函数内部的一块空间上进行赋值操作，给这块空间赋予对应的值，空间大小为4个字节，这里创建了两个变量，所以在main函数中消耗的空间大小就是8个字节；

这里的函数调用过程所创建的新空间会随着函数调用的结束而销毁，因为这里调用的是printf函数，除了printf函数本身需要消耗的空间外并没有出现额外的空间消耗这里我们就不过多探讨。

对这个内容感兴趣的朋友可以回看【函数栈帧的创建与销毁】这一篇的内容，这里面我有通过图片和文字解释对这里的每一步都有进行介绍；

分析到这里我们再来看一下这个代码的空间复杂度$S(n)=O(1)+O(1)=O(1)$；

3.4 代码2

下面我们再来看一个代码：

int main()
{
	int n = 0;//创建一个整型变量n，n所占空间大小为4个字节，对应的空间复杂度为O(1)
	scanf("%d", &n);//调用printf函数——int scanf( const char *format [,argument]... );
	int a = 10;//创建一个整型变量a，a所占空间大小为4个字节，对应的空间复杂度为O(1)
	printf("%d\n", a);//调用printf函数——int printf( const char *format [, argument]... );
	int i = 1;//创建一个整型变量i，i所占空间大小为4个字节，对应的空间复杂度为O(1)
	while (i < n)
	{
		a += i;
		i++;
	}
	printf("%d\n", a);//调用printf函数——int printf( const char *format [, argument]... );
	return 0;
}

在这个代码中，相比于上一个代码，这里多创建了一个变量n，这里的循环次数也是随着n的增大而增大，那它的空间消耗会不会发生变化呢？我们来看一下它的空间消耗情况：

现在我们要观察的是条件判断过程，可以看到此时的条件判断多了一个指令——mov指令——将变量i的值赋值给eax，然后在将变量n的值与eax进行比较。可以看到，这个过程并未额外消耗main函数的空间，所以此时的问题规模n与空间消耗是无关的，所以这个代码的空间复杂度为$S(n)=O(1)+O(1)+O(1)=O(1)$；

3.5 代码3

接下来我们继续看下一个代码：

int main()
{
	int arr[10] = { 1,2,3,4,5,6,7,8,9,10 };//创建一个整型数组arr，arr所占空间大小为40个字节，对应的空间复杂度为O(1)
	int i = 0;//创建一个整型变量i，i所占空间大小为4个字节，对应的空间复杂度为O(1)
	while (i < 10)
	{
		printf("%d  ", arr[i]);//调用printf函数——int printf( const char *format [, argument]... );
		i++;
	}
	return 0;
}

对于这个代码，我们定义了一个大小为10的整型数组和一个变量i，它此时的空间消耗又会是什么样子呢？

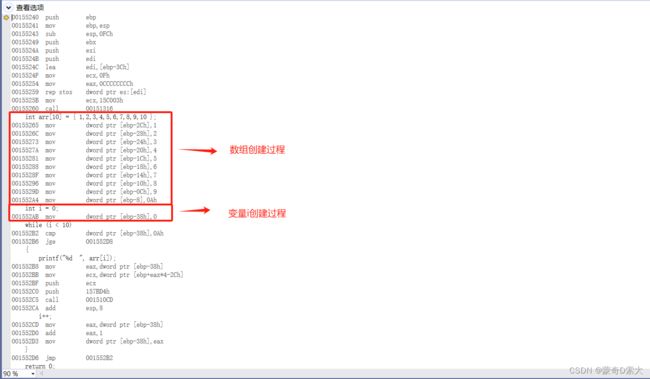
在这个代码中会对main函数的空间进行消耗的就是数组和变量i，所以我们只需要关注它们两个的创建过程就可以了。
对于数组大小为10的整型数组来说，它在main函数中消耗了10个大小为4个字节的空间，对于变量i来说，它在main函数中消耗了1个大小为4个字节的空间。所以这个代码的空间复杂度为$S(n)=O(1)+10\ast O(1)=O(1)$；

如果此时我将数组改一个变长数组int arr[n];那对于这个变长数组而言，它所消耗的空间大小就取决于n的值，所以对于代码：

int main()
{
	int arr[n];//创建一个整型变长数组arr，arr所占空间大小为4*n个字节，对应的空间复杂度为O(n)
	scanf("%d", &n);//调用printf函数——int scanf( const char *format [,argument]... );
	int i = 0;//创建一个整型变量i，i所占空间大小为4个字节，对应的空间复杂度为O(1)
	while (i < 10)
	{
		printf("%d  ", arr[i]);//调用printf函数——int printf( const char *format [, argument]... );
		i++;
	}
	return 0;
}

它的时间复杂度则是$S(n)=O(n)$；

PS：我自己使用的编程环境是VS2019，不支持变长数组，所以这里无法给大家展示这个代码的空间消耗情况。

3.6代码4

接下来我们再看一组代码：

//计算n！
int Func(int n)//创建一个整型变量n，n所占空间大小为4个字节，对应的空间复杂度为O(1)
{
	if (n > 1)
		return n * Func(n - 1);//函数递归，每次调用函数Func都会重新开辟一块新的空间
	return 1;
}
int main()
{
	int n = 0;//创建一个整型变量n，n所占空间大小为4个字节，对应的空间复杂度为O(1)
	scanf("%d", &n);//调用printf函数——int scanf( const char *format [,argument]... );
	int ret = Func(n);//创建一个整型变量ret，ret所占空间大小为4个字节，对应的空间复杂度为O(1)
	printf("%d\n", ret);//调用printf函数——int printf( const char *format [, argument]... );
	return 0;
}

这个代码中通过函数递归的方式来计算n的阶乘，这里我们来依次分析；

• 首先是main函数内部的空间复杂度，经过前面的介绍我们可以很容易得到$S(n)=O(1)$；
• 接下来我们要重点关注的是Func函数的空间复杂度；

对于Func函数来说，它的调用次数取决于n的值；
当n=1时，函数调用1次；当n=2时，函数调用2次；当n=n时，函数调用n次；

下面我们来观察调用一次函数时的空间消耗；

可以看到，对于调用函数时的空间消耗，主要在函数调用刚开始的函数栈帧创建过程。
也就是说，每调用一次函数，就要为函数开辟一块空间；
那我们就不难得到结论：

• 调用一次就开辟一块，调用n次就开辟n块

所以这个代码的空间复杂度为$S(n)=O(n)+O(1)=O(n)$；

归纳总结

对于空间复杂度而言，问题规模并不能直接影响算法的空间复杂度；

• 如上述介绍的代码2，这时无论n的值为多大，只要是在一个整型空间大小的范围内，它的空间复杂度都是$O(1)$；

算法的空间复杂度只取决于问题本身；

• 如代码3和代码4，当这个问题本身涉及到的内容是会消耗空间时，这时的空间复杂度才会随着问题规模的变化而发生相应的变化，此时的空间复杂度就与问题规模有关。

因此我们在计算空间算法的空间复杂度时，只需要关注问题本身是否会消耗除程序之外的额外空间；

结语

到这里，我们对数据结构的绪论中的内容就全部介绍完了，为了更好的理解这些内容，这个期间我自己也是尽可能的在学习相关知识点，从这四个章节的内容看来，其实对于算法而言，最重要的还是时间复杂度的计算，我们一定要掌握时间复杂度的分析方法和步骤。在进入线性表的内容之前，我会再花一个篇章的内容通过习题来介绍如何计算时间复杂度。
最后感谢各位的翻阅，咱们下一篇再见！

【数据结构】第一章——绪论

【数据结构】第一章——绪论（1）：【数据结构的基本概念】

• 本章内容介绍了数据结构的基本概念和术语以及数据结构的三要素

【数据结构】第一章——绪论（2）：【算法】

• 本章介绍了算法的基本概念

【数据结构】第一章——绪论（3）：【时间复杂度】

• 本章详细介绍了算法的时间复杂度

【数据结构】第一章——习题演练：【时间复杂度的分析方法与步骤】

• 本章详细介绍了算法的时间复杂度的分析方法与步骤