C++算法之快速排序

C++算法之快速排序

---

---

一、快速排序引出

我们知道，给一个长度为n的序列排序，有三种很简单的算法：选择排序、冒泡排序、插入排序。这三种算法的复杂度均为O(n^2)。

如果按照计算机1秒钟可以进行10^8次计算作为参照，那么它1秒之内可以排序的序列长度大概为10^4这个数量级。

然而，在实际生活中，10^4级别并不是一个很大的数字，比如说山东每年会有超过50万人参加高考。如果我们想将山东省内所有学生按照高考成绩排序的话，使用O(n^2)将会运行：

不得不说，这样的算法并不算高效。那么，我们能不能设计出更高效的算法呢？

• 一种优化方法
  假设现在，我们只想对1~n的数字排序。并且现在我们有个排序算法，运行复杂度刚好是n^2。

如果：

先把该序列分成两部分，一部分是1~(n/2)，另一部分是(n/2+1)~n；

然后对两个序列进行分别排序 ；

最后再将两部分贴在一起，这个算法的复杂度是多少呢？

1、首先，我们将序列分为长度相等的大小两部分。

此时我们需要将所有<=n/2的数字调出来放到一边;

将所有>n/2的数字挑出来放到另一边;

这个步骤相当于将所有数字看一遍，所以复杂度是O(n)。

2、然后，我们使用原来掌握的排序算法，分别给分好的两个序列排序。

因为两个序列的长度都是n/2，所以两边排序的复杂度都是(n/2)² = n² / 4。两部分排序的总复杂度是(n² / 4) * 2 = n² / 2。

3、最后，我们需要把两部分的排序结果贴在一起。

这个操作几乎不费时间。

所以，我们最终复杂度将是n^2 / 2 + n。和原来直接运行排序算法得到复杂度为n^2 相/比，我们节省了近一半的时间！

由此，我们只需要将原序列划分一下，两边分别排序，最后将该序列合并，就能节省一半的时间（此时因为复杂度仍为平方级别，所以，我们只是在原算法的基础上优化一个常数）。

那么，我们能不能进一步优化该算法呢？

答案是可以的，只要我们按照上述步骤继续分下去就可以了，如下图：

---

二、快排步骤

当然快速排序也可用来给任意n个数的序列排序。但是与和1~n排序不同的是，对于任意n个数的序列，我们在划分子段的时候并不能很容易找到整个序列的“中位数”。所以只能在序列中任意取一个数。比如

• 取整个序列中最左边的数。
• 取整个序列中最右边的数。
• 在整个序列中随机一个位置并取该位置上的数。

都是常见的取数策略。

但由于不能保证每次取的数字都刚好是中位数，所以每次划分时也不能保证左边子段长度和右边子段长度非常平均。如果“不幸”选到不合适的数（比如整个子段中最小的数或最大的数），整个算法的效率会降低很多。

在此，我们详细描述一下给任意n个数排序的快速排序算法：

1、假设我们要对数组a[1..n]排序。初始化区间[1..n] 。

2、令l和r分别为当前区间的左右端点。下面假设我们对l到r子段内的数字进行划分。取pivot = a[l]为分界线，将的数字移到左边，>pivot的数字移到右边，然后将pivot放在中间。假设pivot的位置是k。

3、如果左边区间[l..k-1]长度大于1，则对于新的区间[l..k-1]，重复调用上面的过程。

4、如果右边区间[k+1..r]长度大于1，则设置新的区间[k+1, r]，重复调用上面的过程。

当整个过程结束以后，整个序列排序完毕。

---

三、代码实现

代码如下（示例）：

// 该代码参考 https://www.geeksforgeeks.org/quick-sort/
#include 
#define N 100010 
using namespace std; 
int n; 
int a[N]; 
 
void quick_sort(int l, int r) { 
    // 设置最右边的数为分界线
    int pivot = a[r];
    
    // 元素移动
    int k = l - 1;
    for (int j = l; j < r; ++j)
        if (a[j] < pivot) swap(a[j], a[++k]); 
    swap(a[r], a[++k]); 
    
    if (l < k - 1) quick_sort(l, k - 1); // 如果序列的分界线左边的子段长度>1，排序
    if (k + 1 < r) quick_sort(k + 1, r); // 如果序列的分界线右边的子段长度>1，排序
    // 上面的过程结束后，到这里左子段和右子段已经分别排好序。又因为确定分界线以后的移动操作
    // 保证了左子段中的元素都小于等于分界线，右子段中的元素都大于分界线。所以整个序列也是有序的。
} 
 
int main() { 
    // 输入
    scanf("%d", &n); 
    for (int i = 1; i <= n; ++i) scanf("%d", &a[i]); 
     
    // 快速排序
    quick_sort(1, n); 
    
    // 输出
    for (int i = 1; i <= n; ++i) printf("%d ", a[i]);  
    return 0; 
} 

---

四、复杂度分析

空间复杂度

首先该算法的空间复杂度是O(n)，具体来说，在整个排序过程中，元素的移动都在原始数组中进行。所以快速排序是一种原地排序算法。

时间复杂度

可以看出，在「详细算法描述」中，我们的算法分为若干层。每一层中都是分治法的三个步骤：我们首先进行问题拆分，然后进入下一层，下一层的问题解决后，我们返回这一层进行子问题解的合并。

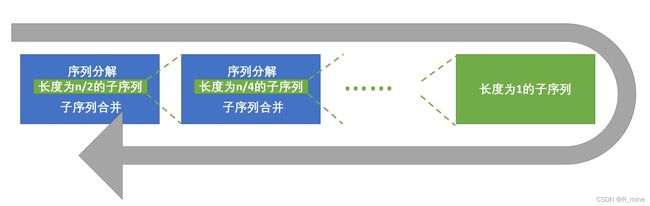
我们首先分析对1~n的n个数字进行快速排序的情况。

在每一层中，问题拆分的复杂度是O(n)，因为我们移动数组元素的时候，需要将每个子段扫一遍。那么把所有层的子段一起看，就相当于在每一层都把整个序列完整扫了一遍。对于子段解的合并，其复杂度是O(1)，因为有分界线的存在，当我们把左边和右边都排好序后，它们和分界线元素一起天然形成了原序列的完整排序。

那么一共有多少层呢？因为每次我们都知道当前子段的中位数，所以可以保证每次划分，两个字段长度比较平衡，所以下一层子段的长度都比上一层减少了一半，直到长度为1算法停止。所以整个算法有logn层。

那么我们分析出在这种情况下，算法的复杂度是O(n * logn)。这样，在1秒之内，计算机能非常轻松地排序10^6 及以上的数据。

但对于任意n个数的排序，每次划分情况取决于选取的分界线情况。如果每次分界线刚好取到最小值或者最大值，会导致划分时所有数字都会移动到同一边，整个算法的复杂度也会下降为O(n^2)。如下图：

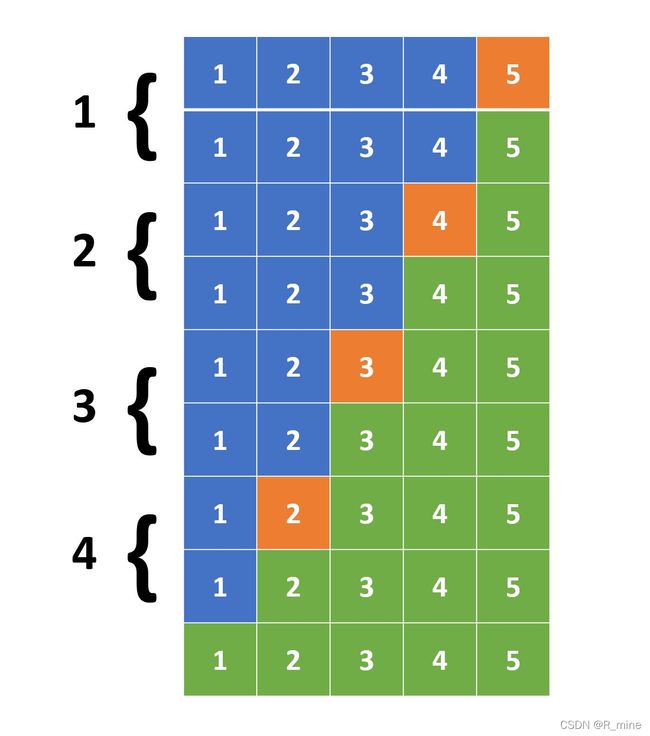
我们很容易想到两种尽量避免出现这种情况的方法：

• 在排序之前，先把整个数组随机打乱顺序。
• 在选取分界线时，与之前固定选取某个位置的方法相比，我们换成随机选择分界线的位置。

这两种方法都能极大概率避免上面提到的极端情况的发生。