CGAL的四叉树、八叉树、正交树

        四叉树（Quadtree）：四叉树是一种用于二维空间分割的数据结构。它将一个二维区域划分为四个象限，每个象限进一步细分为四个小块，以此类推。四叉树可以用于空间索引、图形学、地理信息系统（GIS）等领域。

        八叉树（Octree）：八叉树是四叉树的扩展，用于三维空间分割。它将一个三维区域划分为八个象限，每个象限进一步细分为八个小的三维体，以此类推。八叉树广泛应用于计算机图形学、虚拟现实、空间索引和机器学习等领域。

        正交树（Orthtree）：正交树是一种用于二维或三维空间分割的数据结构，其特点是每个节点代表一个正交区域，即各边相互垂直。正交树的分割方式使得它对于某些特定的几何形状（如矩形或立方体）特别有效。正交树在计算机图形学、空间索引和科学计算等领域有应用。

1、介绍

        四叉树是一种树形数据结构，其中每个节点都包含一个方形空间，每个内部节点都有四个孩子。八叉树是一种类似的3D数据结构，其中每个节点都包含一个立方体空间，每个内部节点都有八个孩子。

        我们将这种数据结构的泛化称为“正交树”，因为正交体是四分体和八分体的泛化。在文献中也可以找到“超八分树”一词，用于命名4维及更高维度的此类数据结构。

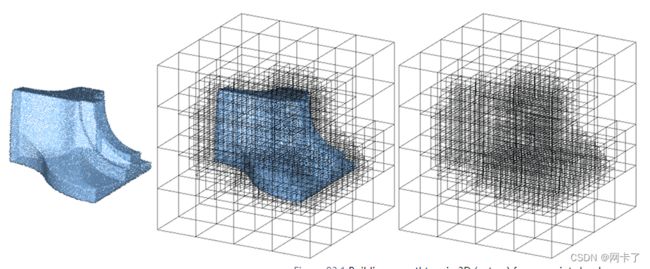
        此软件包提供了一个通用的数据结构 Orthtree 以及 Quadtree 和 Octree 的别名。这些树可以用自定义点范围和分割谓词构造，并使用各种遍历方法迭代。下图是从点云构造八叉树。

2、构造

        使用一组点创建正交树。这些点不会被复制：直接使用提供的点范围，并由正交树重新排列。在创建正交树后更改点范围可能会使其处于无效状态。构造函数返回一个包含所有点的单个（根）节点的树。

        必须调用 refine() 方法来进一步细分空间。此方法使用一个 split 谓词，该谓词以节点为输入，如果该节点应该被分割，则返回 true，否则返回 false：这使得用户可以选择正交树应该细分的标准。提供了预定义的谓词，如 Maximum_depth 或 Maximum_number_of_inliers。

        创建正交树最简单的方法是使用点向量。构造函数通常需要单独的点范围和映射，但如果未提供点映射，则默认使用Identity_property_map。

        分裂谓词是一个用户定义的函子，用于确定节点是否需要分裂。如果现有谓词不符合用户需求，可以很容易地定义自定义谓词。

2.1、构建四叉树

        Orthtree 类可以用 Orthtree_traits_2 进行模板化，从而表现为四叉树。为方便起见，提供了别名 Quadtree。

        以下示例显示了如何从 Point_2 对象的向量创建四叉树对象并对其进行细化，这意味着使用最大深度 10 和每个节点的最大内含线数（桶大小）5 来构造树的空间细分本身。一旦违反其中一个条件，细化就会停止：如果节点的内含线数大于桶大小，但已经达到最大深度，则不会进行分割。同样，深度小于最大深度但内含线数小于桶大小的节点也不会进行分割。

  Quadtree quadtree(points_2d);
  quadtree.refine(10, 5);

2.2、构建八叉树

        Orthtree 类可以用 Orthtree_traits_3 模板化，从而表现为八叉树。为方便起见，提供了别名 Octree。

        以下示例显示了如何从 Point_3 对象的向量创建八叉树。

  // Create an octree from the points
  Octree octree(points);
  // Build the octree
  octree.refine(10, 20);

3、遍历

        为了简单起见，用户手册的其余部分将仅使用八叉树，但所有呈现的功能也适用于四叉树和更高维的正交树。遍历是在树的节点之间导航的行为。 Orthtree 和 Node 类为遍历树提供了许多不同的解决方案。

3.1、手动遍历

        因为我们的正则树是一种连接的无环无向图，所以可以在任意两个节点之间导航。这在实践中意味着，给定树上的一个节点，可以使用正确的操作集访问任何其他节点。Node类提供了一些函数，使用户能够访问它的每个子节点以及它的父节点（如果存在的话）。

        从根节点开始，可以使用下标运算CGAL::Orthtree::Node::operator[]()访问子节点。对于八叉树，0-7的值可以访问不同的子节点。

        对于非根节点，可以使用 parent() 访问器访问父节点。

  std::cout << "the root node: " << std::endl;
  std::cout << octree.root() << std::endl;
  std::cout << "the first child of the root node: " << std::endl;
  std::cout << octree.root()[0] << std::endl;
  std::cout << "the fifth child: " << std::endl;
  std::cout << octree.root()[4] << std::endl;
  std::cout << "the fifth child, accessed without the root keyword: " << std::endl;
  std::cout << octree[4] << std::endl;
  std::cout << "the second child of the fourth child: " << std::endl;
  std::cout << octree.root()[4][1] << std::endl;
  std::cout << "the second child of the fourth child, accessed without the root keyword: " << std::endl;
  std::cout << octree[4][1] << std::endl;
  std::cout << std::endl;

3.2、前序遍历

        能够以特定的顺序遍历树的节点通常很有用。例如，流运算符<<使用遍历来打印出每个节点。提供了几种遍历，其中包括Preorder_traversal和Postorder_traversal。以预序遍历树是立即访问每个父节点，然后访问其子节点，而在后序中，首先访问子节点。

  Octree octree(points, points.point_map());
  octree.refine();
  for (Octree::Node node : octree.traverse()) {
    std::cout << node << std::endl;
  }

3.3、自定义遍历

        用户可以通过创建 OrthtreeTraversal 概念的模型来定义自己的遍历方法。

3.4、图解

        显示了根据所使用的遍历方法访问节点的顺序。

        四叉树以图形形式显示。每个节点都根据遍历访问的顺序进行标记。使用叶子和级别遍历时，四叉树仅被部分遍历。 

4、任务加速

        一旦构建了正交树，它的结构就可以用来加速不同的任务。

4.1、寻找点的最近邻

        找到一个点的最近邻的朴素方法需要找到到每个其他点的距离。正交树可以在更短的时间内完成相同的任务。对于大量的点，这可能是一个足够大的差异，超过了构建树所花费的时间。

        请注意，kd-tree在这个任务上预计会优于orthtree，除非需要orthtree特有的功能，否则应该首选kd-tree。

4.2、分级

        如果每对叶子之间相邻两片叶子之间的深度差最多为1，则正树是分级的。

        使用 grade 方法消除 orthtree 中深度的大幅跳跃。

        一棵树的创建方式是，一个节点的分裂次数比它相邻的节点多得多。 grade() 拆分八叉树的节点，使相邻节点的深度差不超过 1。在分级前后打印树，以便可以看到差异。

5、性能

5.1、构建性能

        树构建基准是通过随机生成一组点来完成的，然后对创建包含这些点的完全精炼树的过程进行计时。由于其简单性，八叉树可以比kd树更快地构建。

5.2、查找最近邻的性能

        正交树节点是均匀的，因此正交树往往比等效的kd树具有更深的层次结构。因此，正交树在最近邻搜索方面的性能通常较差。两种最近邻算法的理论复杂度均为O(log(n))，但正交树通常可以预期具有更高的系数。

        这两棵树之间的性能差异很大，但与涉及将每个点与搜索点进行比较的朴素方法的线性复杂度相比，这两种算法都非常有利。

        使用正交树进行最近邻计算而不是kd树，可以在需要很少查询时（因为构造更快）或正交树也需要其他用途时进行证明。 

         对于大数量级的点计数，朴素方法的计算时间远远超过正交树或kd树的计算时间。

CGAL 5.6 - Quadtrees, Octrees, and Orthtrees: User Manual