ｃ语言实现数据结构中的队列

队列的概念

我们在上一篇文章讲了栈的概念，我们说栈的特点是他只允许在固定的一段进行插入和删除元素的操作，我们把数据插入和删除的一端称为栈顶，另一端称为栈底，栈中的数据遵守后进先出的LIFO原则，那我们的队列呢？队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out) 入队列：进行插入操作的一端称为队尾 。出队列：进行删除操作的一端称为队头。那这么看的话我们的队列就与我们的栈式相反的他是先进先出，而我们的栈是后进先出，那么我们这里就来看看队列是如何来实现的。

队列的准备

首先我们来思考一个问题就是我们这里的队列采用什么样的方式来实现，是用顺序表还是链表呢？我们之前的栈为什么采用顺序表呢？是不是因为我们的栈是尾插尾删啊，他的操作都在尾部，而刚好我们的顺序表在对尾部的操作的时间复杂度都是o(1)就非常的方便所以我们采用顺序表来实现栈，但是我们这里的队列那就有点点冲突，他需要头部出数据，尾部插入数据，所以我们这里即要对头部操作，也要对尾部操作，但是我们的顺序表有一个缺点就是对头部的操作效率都非常地低，所以我们这里就不采用顺序表，采用链表，但是这时候有小伙伴们说：啊！链表的尾插尾删不是也很麻烦吗？要找尾啥的，但是这个问题很容易解决我们直接创建一个结构体，在结构体里面放两个变量一个用来记录链表的头部，一个用来记录链表的尾部，这样的话我们就可以不用找尾了，效率大大的提升，那么我们的代码如下：

typedef int QDataType;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType x;
}Qnode;

typedef struct Queue
{
	 Qnode* head;
	 Qnode* tail;
}Queue;

队列的初始化

根据之前的学习我们知道链表是没有初始化这个功能的，那我们的队列有初始化的功能吗？答案是有的，但是我们不对存储数据的那个结构体进行操作，我们对控制队列的那个结构体进行操作，将这个结构体里面的两个指针全部都初始化为NULL，那么我们的代码就如下：

void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
}

队列的销毁

既然我们创建了一个队列，那么等我们不用这个数列的时候我们就得将这个队列进行销毁，那么我们这里的链表他是循环申请空间的，不是一下子开辟一个大的空间吗，所以我们这里在销毁的时候就得循环的释放空间，并且还得将控制队列的结构体里面的两个指针也都初始化为空，那么我们的代码就如下：

void QueueDestory(Queue* pq)
{
	assert(pq);
	Qnode* cur = pq->head;
	while (cur != NULL)
	{
		Qnode* del = cur;
		free(del);
		cur = cur->next;
	}
	pq->head = pq->tail = NULL;
}

队列的插入

我们知道了如何销毁队列如何初始化队列，那么我们这里就来看看如何往队列里面插入数据，首先我们肯定得创建一个节点出来，因为队列的插入是尾插，所以我们这里就通过结构体里面的tail来找到队列尾部，再将新创建出来的节点与尾部连接起来，啊这里的连接就是将最后一个节点中的next指针指向我们新创建出来的节点，这样我们就实现了尾插，最后再更改一下我们结构体中tail的值将他指向新的尾部，这样我们就实现了队列的插入，但是我们上面说的这个方法是争对队列中已经存在元素的情况，如果我们的链表中没有元素的话我们就得将这个结构体里面的两个指针全部指向我们新创建出来的节点，那么我们这里就得分情况而论，我们的代码就如下：

void QueueInsert(Queue* pq,QDataType x)
{
	assert(pq);
	Qnode* newnode = (Qnode*)malloc(sizeof(Qnode));
	newnode->next = NULL;
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	
	if (pq->head == NULL)
	{
		pq->head = pq->tail = newnode;
		
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}
	newnode->x = x;

}

队列的删除

队列的删除是在头部进行的删除，所以我们这里的删除就相当于链表的头删，那么我们在执行删除操作之前就得先判断一下我们这里的链表是否还有元素可以删除，我们这里的判断就是断言一下，如果我们这里的两个指针只要有一个为空，那么这就说明我们的队列此时已经没有了元素，不能再删除了，好判断完之后我们再来执行删除操作，我们这里的删除就是将头部指针指向的元素释放掉，然后再将头部指向指向它的下一个元素，但是我们这里有一种情况就是当我们的队列只有一个元素的时候我们这里再删除就得将两个指针的内容就全部都置为空，那么我们这里的代码就如下：

void QueuePop(Queue* pq)
{
	assert(pq);
	assert(pq->head);
	if (pq->head == pq->tail)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		Qnode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}
}

获取队列的个数

我们这里的获取队列的个数也很简单，我们可以创建一个循环和一个变量，在这个循环里面进行遍历并且用这个变量来记录我们链表中元素的个数，那么我们这个循环结束的条件就是当我们遍历到指针变量为空的时候我们就跳出了循环，那么我们的代码就如下：

int QueueSize(Queue* pq)
{
	assert(pq);
	Qnode* cur = pq->head;
	int size = 0;
	while (cur != NULL)
	{
		size++;
		cur = cur->next;
	}
	return size;
}

获取队列的头部或者尾部的元素

我们这里的获取头部或者尾部的元素就可以直接通过我们这里结构体中的头部指针和尾部指针来获取，然后我们将其作为函数的返回值，那么我们的代码就如下：

int QueueFront(Queue* pq)
{
	assert(pq);
	return pq->head->x;
}
int QueueBack(Queue* pq)
{
	assert(pq);
	return pq->tail->x;
}

那么看到这里我们队列的实现就结束了，那么我们上面的代码实现是正确的吗？我们可以用下面的代码进行一下测试：

#include"Queue.h"
int main()
{
	Queue QL;
	QueueInit(&QL);
	QueueInsert(&QL, 10);
	QueueInsert(&QL, 20);
	QueueInsert(&QL, 30);
	QueueInsert(&QL, 40);
	QueueInsert(&QL, 50);
	QueueInsert(&QL, 60);
	QueueInsert(&QL, 70);
	printf("此时头顶的元素为%d\n", QueueFront(&QL));
	printf("此时尾部的元素为%d\n", QueueBack(&QL));
	printf("此时链表的元素个数为%d\n", QueueSize(&QL));
	QueuePop(&QL);
	QueueInsert(&QL, 80);
	printf("此时头顶的元素为%d\n", QueueFront(&QL));
	printf("此时尾部的元素为%d\n", QueueBack(&QL));
	QueuePop(&QL);
	printf("此时链表的元素个数为%d\n", QueueSize(&QL));
	QueueDestory(&QL);
	return 0;
}

那么我们这里的代码运行的结果就如下：

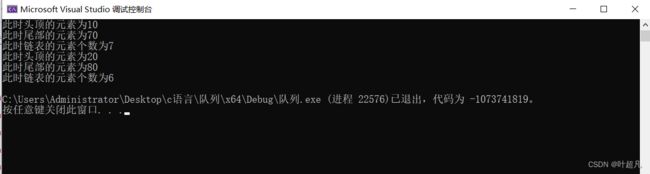
看样子我们代码的实现是正确的，那么我们的队列就实现成功了，因为我们的队列是根据链表来实现的，因为链表我们之前详细的讲过所以我们这里讲的就比较的简介哈，如果有不懂的可以先看看链表的那篇文章。
点击此处获取代码