Pure-Pursuit 跟踪五次多项式轨迹

Pure-Pursuit 跟踪五次多项式轨迹

考虑双移线轨迹 X 轴方向位移较大，机械楼停车场长度无法满足 100 ~ 120 m，因此采用五次多项式进行轨迹规划，在轨迹跟踪部分也能水一些内容

调整 double_lane.cpp 为 ref_lane.cpp，结合 FrenetPath 类将参考路径的构造抽离为单独的函数

#include 
#include 
#include 
#include 
#include 

#include 
#include 
#include 
#include 
#include 
#include 

#include "cpprobotics_types_double.h"
#include "frenet_path_double.h"
#include "quintic_polynomial_double.h"

using namespace std;
using namespace cpprobotics;

// 双移线参考路径在 X 方向长度以及参考点的步长
const float length = 120.0;
const float step = 0.1;

// 五次多项式轨迹参数
#define DT 0.01
const double T = 50.0; // t-t0经历的时间
const double xend = 25.0;
const double yend = 3.0;

array<float, 4> calEulerToQuaternion(const float roll, const float pitch, const float yaw)
{
    array<float, 4> calQuaternion = {0.0f, 0.0f, 0.0f, 1.0f}; // 初始化四元数

    // 使用Eigen库来进行四元数计算
    Eigen::Quaternionf quat;
    quat = Eigen::AngleAxisf(roll, Eigen::Vector3f::UnitX()) *
           Eigen::AngleAxisf(pitch, Eigen::Vector3f::UnitY()) *
           Eigen::AngleAxisf(yaw, Eigen::Vector3f::UnitZ());

    calQuaternion[0] = quat.x();
    calQuaternion[1] = quat.y();
    calQuaternion[2] = quat.z();
    calQuaternion[3] = quat.w();

    return calQuaternion;
}

FrenetPath fp;
void calc_frenet_paths()
{
    // 起始状态
    std::array<double, 3> x_start{0.0, 0.0, 0.0};
    std::array<double, 3> x_end{xend, 0.0, 0.0};
    // 终点状态
    std::array<double, 3> y_start{0.0, 0.0, 0.0};
    std::array<double, 3> y_end{yend, 0.0, 0.0};

    // 纵向
    QuinticPolynomial lon_qp(x_start[0], x_start[1], x_start[2], x_end[0],
                             x_end[1], x_end[2], T);
    // 横向
    QuinticPolynomial lat_qp(y_start[0], y_start[1], y_start[2], y_end[0],
                             y_end[1], y_end[2], T, xend);

    for (double t = 0; t < T; t += DT)
    {
        double x = lon_qp.calc_point_x(t);
        double xd = lon_qp.calc_point_xd(t);
        double xdd = lon_qp.calc_point_xdd(t);

        fp.t.emplace_back(t);
        fp.x.emplace_back(x);
        fp.x_d.emplace_back(xd);
        fp.x_dd.emplace_back(xdd);

        double y_x_t = lat_qp.calc_point_y_x(x);
        double y_x_d = lat_qp.calc_point_y_x_d(x);
        double y_x_t_d = lat_qp.calc_point_y_t_d(y_x_d, xd);

        double y_x_dd = lat_qp.calc_point_y_x_dd(x);
        double y_x_t_dd = lat_qp.calc_point_y_t_dd(y_x_dd, xd, y_x_d, xdd);

        fp.y.emplace_back(y_x_t);
        fp.y_d.emplace_back(y_x_t_d);
        fp.y_dd.emplace_back(y_x_t_dd);
        // 压入航向角
        // fp.threat.emplace_back(lat_qp.calc_point_thetar(y_x_t_d, xd));

        // 压入曲率
        fp.k.emplace_back(lat_qp.calc_point_k(y_x_dd, y_x_d));
        // fp.k.emplace_back(lat_qp.calc_point_k(y_x_t_dd, y_x_t_d, xdd, xd));
    }
    int num = fp.x.size();
    for (int i = 0; i < num; i++)
    {
        double dy = fp.y[i + 1] - fp.y[i];
        double dx = fp.x[i + 1] - fp.x[i];
        fp.threat.emplace_back(lat_qp.calc_point_thetar(dy, dx));
    }
    // 最后一个道路航向角和前一个相同
    // fp.threat.push_back(fp.threat.back());
}

void double_lane_path()
{
  // 双移线构造的参数
  const float shape = 2.4;
  const float dx1 = 25.0, dx2 = 21.95;
  const float dy1 = 4.05, dy2 = 5.7;
  const float Xs1 = 27.19, Xs2 = 56.46;

  int points_size = length / step;
  fp.x.resize(points_size);
  fp.y.resize(points_size);
  fp.threat.resize(points_size);
  fp.k.resize(points_size);
  for (int i = 0; i <= points_size; ++i)
  {
    // 计算参考路径点信息
    float ref_x = i * step;
    float z1 = shape / dx1 * (ref_x - Xs1) - shape / 2.0;
    float z2 = shape / dx2 * (ref_x - Xs2) - shape / 2.0;
    float ref_y = dy1 / 2.0 * (1 + tanh(z1)) - dy2 / 2.0 * (1 + tanh(z2));
    float ref_phi = atan(pow(dy1 * (1 / cosh(z1)), 2) * (1.2 / dx1) - pow(dy2 * (1 / cosh(z2)), 2) * (1.2 / dx2));

    float y_dot = dy1 / 2 * pow(1 / cosh(z1), 2) * (shape / dx1) - dy2 / 2 * pow(1 / cosh(z2), 2) * (shape / dx2);
    float y_ddot = -2 * dy1 * ((cosh(z1) - 1) / pow(cosh(z1), 3)) * pow(shape / dx1, 2) + 2 * dy2 * ((cosh(z2) - 1) / pow(cosh(z2), 3)) * pow(shape / dx2, 2);
    float ref_k = abs(y_ddot) / pow(1 + y_dot * y_dot, 1.5);
    
    fp.x[i] = ref_x;
    fp.y[i] = ref_y;
    fp.threat[i] = ref_phi;
    fp.k[i] = ref_k;
  }
}

int main(int argc, char *argv[])
{
    ros::init(argc, argv, "ref_lane");

    ros::NodeHandle nh;
    ros::Publisher path_pub = nh.advertise<nav_msgs::Path>("/ref_path", 1000, true);

    nav_msgs::Path reference_path;
    reference_path.header.frame_id = "world";
    reference_path.header.stamp = ros::Time::now();

    geometry_msgs::PoseStamped pose;
    pose.header.stamp = ros::Time::now();
    pose.header.frame_id = "world";

    // 五次多项式轨迹
    calc_frenet_paths();

    // 双移线轨迹
    // double_lane_path();

    int points_size = fp.x.size();
    reference_path.poses.resize(points_size);
    for (int i = 0; i < points_size; ++i)
    {        
        cout << fp.x[i] << "," << fp.y[i] << "," << fp.threat[i] << endl;
        // 计算四元数位姿
        array<float, 4> calQuaternion = calEulerToQuaternion(0.0, 0.0, fp.threat[i]);

        pose.pose.position.x = fp.x[i];
        pose.pose.position.y = fp.y[i];
        pose.pose.position.z = 0.0;
        pose.pose.orientation.x = calQuaternion[0];
        pose.pose.orientation.y = calQuaternion[1];
        pose.pose.orientation.z = calQuaternion[2];
        pose.pose.orientation.w = calQuaternion[3];
        reference_path.poses[i] = pose;
    }

    ros::Rate loop(10);
    while (ros::ok())
    {
        path_pub.publish(reference_path);
        ros::spinOnce();
        loop.sleep();
    }

    return 0;
}

跟踪过程如下

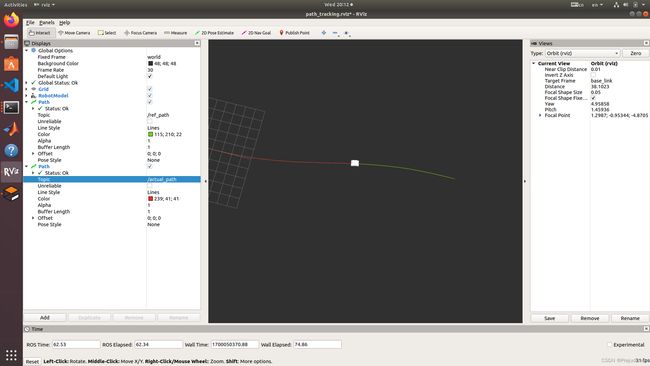
跟踪效果如下

这里只分析出横向跟踪误差，因为 y 与 x 的关系可以直接获得，yaw 与 x 的关系没有直接的表达式

y = 0.00000000 + 0.00000000 * x + 0.00000000 * x^2 + 0.00192000 * x^3 + -0.00011520 * x^4 + 0.00000184 * x^5

需要完善对于五次多项式的学习