【代码随想录刷题】Day20 二叉树06
文章目录
- 1.【654】最大二叉树
-
- 1.1 题目描述
- 1.2 解题思路
- 1.3 java代码实现
- 1.4 总结
- 2.【617】合并二叉树
-
- 2.1 题目描述
- 2.2 解题思路
- 2.3 java代码实现
- 3.【700】二叉搜索树中的搜索
-
- 3.1 题目描述
- 3.2 解题思路
- 3.3 java代码实现
- 4.【98】验证二叉搜索树
-
- 4.1 题目描述
- 4.2 解题思路
- 4.3 java代码实现
【654】最大二叉树
【617】合并二叉树
【700】二叉搜索树中的搜索
【98】验证二叉搜索树
1.【654】最大二叉树
【654】最大二叉树
1.1 题目描述
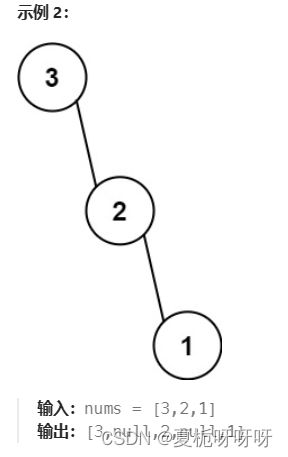
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 1.创建一个根节点，其值为 nums 中的最大值。
- 2.递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 3.递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
解释： 递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
- 空数组，无子节点。
- [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
- 空数组，无子节点。
- 只有一个元素，所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
- 只有一个元素，所以子节点是一个值为 0 的节点。
- 空数组，无子节点。
提示：
- [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
- 1 <= nums.length <= 1000
- 0 <= nums[i] <= 1000
- nums 中的所有整数 互不相同
1.2 解题思路
最大二叉树的构建过程如下：
构造树一般采用的是前序遍历，因为先构造根节点，然后递归构造左子树和右子树。
递归三部曲
-
- 确定递归函数的参数和返回值
参数：存放元素的数组
返回值：返回该数组构造的二叉树的头结点
public TreeNode travesal(int[] nums,int leftIndex,int rightIndex)
-
- 确定终止条件
题目中说了输入的数组大小一定是大于等于1的，所以我们不用考虑小于1的情况，那么当递归遍历的时候，如果传入的数组大小为1，说明遍历到了叶子节点了。
那么应该定义一个新的节点，并把这个数组的数值赋给新的节点，然后返回这个节点。 这表示一个数组大小是1的时候，构造了一个新的节点，并返回。
//没有元素
if (rightIndex-leftIndex<1){
return null;
}
//只有一个元素
if (rightIndex-leftIndex==1){
return new TreeNode(nums[leftIndex]);
}
-
- 确定单层递归的逻辑
这里又要分为三步：
1.先要找到数组中最大的值和对应的下标， 最大的值构造根节点，下标用来下一步分割数组
//最大值所在位置
int maxIndex=leftIndex;
//最大值
int maxVal=nums[maxIndex];
//找最大值
for (int i = leftIndex+1; i < rightIndex; i++) {
if (nums[i]>maxVal){
maxVal=nums[i];
maxIndex=i;
}
}
TreeNode root=new TreeNode(maxVal);
2.最大值所在的下标左区间 构造左子树
3.最大值所在的下标右区间 构造右子树
//根据maxIndex划分左右子树
root.left=travesal(nums,leftIndex,maxIndex);
root.right=travesal(nums,maxIndex+1,rightIndex);
1.3 java代码实现
class Solution {
public TreeNode constructMaximumBinaryTree(int[] nums) {
return travesal(nums,0,nums.length);
}
/**
* 先找出最大元素，即根节点
* 用最大元素来划分左右子树区间
*/
public TreeNode travesal(int[] nums,int leftIndex,int rightIndex){
//没有元素
if (rightIndex-leftIndex<1){
return null;
}
//只有一个元素
if (rightIndex-leftIndex==1){
return new TreeNode(nums[leftIndex]);
}
//最大值所在位置
int maxIndex=leftIndex;
//最大值
int maxVal=nums[maxIndex];
//找最大值
for (int i = leftIndex+1; i < rightIndex; i++) {
if (nums[i]>maxVal){
maxVal=nums[i];
maxIndex=i;
}
}
TreeNode root=new TreeNode(maxVal);
//根据maxIndex划分左右子树
root.left=travesal(nums,leftIndex,maxIndex);
root.right=travesal(nums,maxIndex+1,rightIndex);
return root;
}
}
1.4 总结
此题与【106】从中序与后序遍历序列构造二叉树解题思路是一样的。此题的详细解题思路请看【代码随想录刷题】Day18 二叉树05。
注意类似用数组构造二叉树的题目，每次分隔尽量不要定义新的数组，而是通过下标索引直接在原数组上操作，这样可以节约时间和空间上的开销。
递归函数前面加if的情况：一般情况来说：如果让空节点（空指针）进入递归，就不加if，如果不让空节点进入递归，就加if限制一下， 终止条件也会相应的调整。其实这就是不同代码风格的实现。
2.【617】合并二叉树
【617】合并二叉树
2.1 题目描述
给你两棵二叉树： root1 和 root2 。
想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
提示：
- 两棵树中的节点数目在范围 [0, 2000] 内
- -104 <= Node.val <= 104
2.2 解题思路
本题使用前序遍历。
递归三部曲
-
- 确定递归函数的参数和返回值
首先要合入两个二叉树，那么参数至少是要传入两个二叉树的根节点，返回值就是合并之后二叉树的根节点。
public TreeNode mergeTrees(TreeNode root1, TreeNode root2)
-
- 确定终止条件
因为是传入了两个树，那么就有两个树遍历的节点t1 和 t2，如果t1 == NULL 了，两个树合并就应该是 t2 了（如果t2也为NULL也无所谓，合并之后就是NULL）。
反过来如果t2 == NULL，那么两个数合并就是t1（如果t1也为NULL也无所谓，合并之后就是NULL）。
if(root1==null){
return root2;
}
if (root2==null){
return root1;
}
-
- 确定单层递归的逻辑
我们重复利用一下t1这个树，t1就是合并之后树的根节点（就是修改了原来树的结构）。那么单层递归中，就要把两棵树的元素加到一起。
root1.val+= root2.val;
接下来t1 的左子树是：合并 t1左子树 t2左子树之后的左子树。
t1 的右子树：是 合并 t1右子树 t2右子树之后的右子树。
最终t1就是合并之后的根节点。
root1.left=mergeTrees(root1.left,root2.left);
root1.right=mergeTrees(root1.right,root2.right);
return root1;
2.3 java代码实现
递归
class Solution {
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
if(root1==null){
return root2;
}
if (root2==null){
return root1;
}
root1.val+= root2.val;
root1.left=mergeTrees(root1.left,root2.left);
root1.right=mergeTrees(root1.right,root2.right);
return root1;
}
}
迭代
class Solution {
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
//使用队列迭代
if(root1==null){
return root2;
}
if (root2==null){
return root1;
}
Queue<TreeNode> queue=new LinkedList<>();
queue.offer(root1);
queue.offer(root2);
while (!queue.isEmpty()){
TreeNode node1=queue.poll();
TreeNode node2=queue.poll();
//此时两个节点一定不为空，值val相加
node1.val+=node2.val;
//如果两棵树左节点不为空，加入队列
if (node1.left!=null && node2.left!=null){
queue.offer(node1.left);
queue.offer(node2.left);
}
//如果两棵树右节点不为空，加入队列
if (node1.right!=null && node2.right!=null){
queue.offer(node1.right);
queue.offer(node2.right);
}
//若node1的左节点为空，直接赋值
if (node1.left==null && node2.left!=null){
node1.left=node2.left;
}
//若node1的右节点为空，直接赋值
if (node1.right==null && node2.right!=null){
node1.right=node2.right;
}
}
return root1;
}
}
3.【700】二叉搜索树中的搜索
【700】二叉搜索树中的搜索
3.1 题目描述
给定二叉搜索树（BST）的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。
提示：
- 树中节点数在 [1, 5000] 范围内
- 1 <= Node.val <= 107
- root 是二叉搜索树
- 1 <= val <= 107
3.2 解题思路
首先要知道什么是二叉搜索树。
二叉搜索树是一个有序树：
- 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
- 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
- 它的左、右子树也分别为二叉搜索树
这就决定了，二叉搜索树，递归遍历和迭代遍历和普通二叉树都不一样。
递归法
-
- 确定递归函数的参数和返回值
递归函数的参数传入的就是根节点和要搜索的数值，返回的就是以这个搜索数值所在的节点。
public TreeNode searchBST(TreeNode root, int val)
-
- 确定终止条件
如果root为空，或者找到这个数值了，就返回root节点。
if (root==null || root.val==val){
return root;
}
-
- 确定单层递归的逻辑
看看二叉搜索树的单层递归逻辑有何不同。
因为二叉搜索树的节点是有序的，所以可以有方向的去搜索。
如果root->val > val，搜索左子树，如果root->val < val，就搜索右子树，最后如果都没有搜索到，就返回NULL。
if (val< root.val){
return searchBST(root.left,val);
}else {
return searchBST(root.right,val);
}
迭代法
一提到二叉树遍历的迭代法，可能立刻想起使用栈来模拟深度遍历，使用队列来模拟广度遍历。
对于二叉搜索树可就不一样了，因为二叉搜索树的特殊性，也就是节点的有序性，可以不使用辅助栈或者队列就可以写出迭代法。
对于一般二叉树，递归过程中还有回溯的过程，例如走一个左方向的分支走到头了，那么要调头，在走右分支。
而对于二叉搜索树，不需要回溯的过程，因为节点的有序性就帮我们确定了搜索的方向。
例如要搜索元素为3的节点，我们不需要搜索其他节点，也不需要做回溯，查找的路径已经规划好了。
3.3 java代码实现
递归
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
if (root==null || root.val==val){
return root;
}
if (val< root.val){
return searchBST(root.left,val);
}else {
return searchBST(root.right,val);
}
}
}
迭代
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
//迭代
while (root != null)
if (val < root.val) root = root.left;
else if (val > root.val) root = root.right;
else return root;
return null;
}
}
4.【98】验证二叉搜索树
【98】验证二叉搜索树
4.1 题目描述
给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下：
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
提示：
- 树中节点数目范围在[1, 104] 内
- -231 <= Node.val <= 231 - 1
4.2 解题思路
划重点啦啦啦啦！！！！！！
要知道中序遍历下，输出的二叉搜索树节点的数值是有序序列。
有了这个特性，验证二叉搜索树，就相当于变成了判断一个序列是不是递增的了。
递归法：
可以递归中序遍历将二叉搜索树转变成一个数组，然后只要比较一下，这个数组是否是有序的，注意二叉搜索树中不能有重复元素。
陷阱！！！
陷阱！！！
陷阱！！！
不能单纯的比较左节点小于中间节点，右节点大于中间节点就完事了。
我们要比较的是 左子树所有节点小于根节点，右子树所有节点大于根节点。
比如下图中这种情况：
节点15大于左节点10,2，小于右节点17，但是右子树里出现了一个9这就不符合二叉搜索树了。
递归三部曲:
-
- 确定递归函数，返回值以及参数
用题目中给出的即可
- 确定递归函数，返回值以及参数
-
- 确定终止条件
如果是空节点 是不是二叉搜索树呢？是的，二叉搜索树也可以为空！
if (root==null){
return true;
}
-
- 确定单层递归的逻辑
中序遍历，一直更新max，一旦发现max >= root.val，就返回false，注意元素相同时候也要返回false。
//左
boolean left=isValidBST(root.left);
if (!left){
return false;
}
//根
if (max!=null && root.val<=max.val){
return false;
}
max=root;
//右
boolean right=isValidBST(root.right);
return right;
迭代法：
可以用迭代法模拟二叉树中序遍历，那么此题将迭代法中序遍历稍加改动就可以了。
4.3 java代码实现
递归
- 先判断左子树，若左子树有一个节点不是小于根节点的值，直接返回false
- 若左子树为true，再判断右子树
- 若右子树为true，整个递归直接返回true;若右子树为false，整个递归直接返回false。
class Solution {
TreeNode max;
public boolean isValidBST(TreeNode root) {
//递归
if (root==null){
return true;
}
//左
boolean left=isValidBST(root.left);
if (!left){
return false;
}
//根
if (max!=null && root.val<=max.val){
return false;
}
max=root;
//右
boolean right=isValidBST(root.right);
return right;
}
}
迭代
class Solution {
public boolean isValidBST(TreeNode root) {
//迭代
if (root==null){
return true;
}
Stack<TreeNode> stack=new Stack<>();
TreeNode pre=null;//前一个节点
while (root!=null || !stack.isEmpty()){
while (root!=null){
stack.push(root);
root=root.left;//左
}
//根
TreeNode pop=stack.pop();
if (pre!=null && pop.val<=pre.val){
return false;
}
pre=pop;
//右
root=pop.right;
}
return true;
}
}