【蓝桥杯软件赛 零基础备赛20周】第6周——栈

1. 基本数据结构概述

很多计算机教材提到：程序 = 数据结构 + 算法。

“以数据结构为弓，以算法为箭”

数据结构是是计算机存储、组织数据的方法。常用的数据结构有：数组（Array）、栈（Stack）、队列（Queue）、链表（Linked List）、树（Tree）、图（Graph）、堆（Heap）、散列表（Hash）等。分为两大类：线性表、非线性表。数组、栈、队列、链表是线性表，其他是非线性表。

1.1 数据结构和算法的关系

数据结构和算法往往密不可分。下面以图的存储为例，说明数据结构和算法的关系。这几种存图的数据结构，各有优缺点，也各有自己的应用场景。

（1）边集数组

定义结构体数组：

struct Edge{
     int u, v, w;
}edges[M];

其中(u,v,w)表示一条边，起点是u，终点是v，边长是w。edges[M]可以存M条边。

边集数组的优点：是最节省空间的存图方法，存储空间不可能再少了。n=1000个点，m=5000条边的图，使用的存储空间是12×5000 = 60KB。

边集数组的缺点：不能快速定位某条边。如果要找某点u和哪些点有边连接，得把整个edges[M]从头到尾搜一遍才能知道。

边集数组的的应用场景：如果算法不需要查找特定的边，就用边集数组。例如最小生成树Kruskal算法、最短路径Bellman-ford算法。

（2）邻接矩阵

定义一个二维数组：

	int edge[N][N];

其中edge[i][j]表示点i和点j之间有一条边，边长为edge[i][j]。它可以存N个点的边。若edge[i][j]=0，表示i和j之间没有边；若edge[i][j] != 0，i和j之间有边，边长为edge[i][j]。

邻接矩阵的优点：能极快地查询任意两点之间是否有边。如果edge[i][j] != 0，说明点i和j之间有一条边，边长edge[i][j]。

邻接矩阵的缺点：如果图是一张稀疏图，大部分点和边之间没有边，那么邻接矩阵很浪费空间，因为大多数edge[][]=0，没有用到。n=1000个点，m=5000条边的图，使用的存储空间是12×1000×1000 = 12MB。

邻接矩阵的应用场景：（1）稠密图，几乎所有的点之间都有边，edge[][]数组几乎用满了，很少浪费；（2）算法需要快速查找边，而且计算结果和任意两点的关系有关，例如最短路径算法的Floyd算法。

（3）邻接表

邻接矩阵的优点：十分节省空间，因为只存储存在的边。

邻接矩阵的缺点：没有明显的缺点。它的存储空间只比边集数组大一点点，而查询边的速度只比邻接矩阵慢一点点。

邻接矩阵应用场景：基于稀疏图的大部分算法。

1.2 线性数据结构概述

在所有数据结构中，线性表是最简单的。线性表有数组、链表、队列、栈，它们有一个共同的特征：把同类型的数据一个接一个地串在一起。

下面对线性表做个概述，并比较它们的优缺点。

（1）数组

数组是最最简单的数据结构，它的逻辑结构和物理内存的存储完全一样。例如C语言中定义一个整型数组int a[10]，系统会分配一个40字节的存储空间，这100个字符的存储地址是连续的。

#include 
using namespace std;
int main(){
    int a[10];
    for (int i=0;i<10;i++)  
         cout << &a[i] << " ";  //打印10个整数的存储地址
    return 0;
}

在作者机器上运行，输出10个整数的存储地址：
0x6dfec4 0x6dfec8 0x6dfecc 0x6dfed0 0x6dfed4 0x6dfed8 0x6dfedc 0x6dfee0 0x6dfee4 0x6dfee8

数组的优点：（1）简单，容易编程；（2）访问快捷，要定位到某个数据，只需使用下标即可，例如a[0]是第1个数据，a[i]是第i-1个数据；（3）与某些应用场景直接对应，例如数列是一维数组，可以在一维护数组上排序，矩阵是二维数组，表示空间坐标，等等。

数组的缺点：删除和增加数据很麻烦，非常耗时。例如要删除数组int a[10]的第5个数据，只能采用覆盖的方法，从第6个数据开始，每个往前挪一位。增加数据也麻烦，例如要在第5个位置插入一个数据，只能把原来第5个开始的数据逐个往后挪一位，空出第5个位置给新数据。

（2）链表

链表是为了克服数组的缺点提出的一种线性表，链表的插入和删除操作，不需要挪动其他数据。简单地说，链表是“是用指针串起来的数组”。链表的数据不是连续存放的，而是用指针串起来的。例如下图删除链表的第3个数据，只要把原来连接第3个数据的指针断开，然后连接它前后的数据即可，不用挪动其他的数据。

链表的优点：增加和删除数据很便捷。这个优点弥补了数组的缺点。

链表的缺点：定位某个数据比较麻烦。例如要输出第5个数据，需要从链表头开始，沿着指针一步步走，找到第5个。链表的这个缺点却是数组的优点。

链表和数组的优缺点正好相反，它们的应用场合不同，数组适合静态数据，链表适合动态数据。

链表如何编程实现？在常见的数据结构教材中，链表的数据节点是动态分配的，各节点之间用指针来连接。但是在算法竞赛中，如果手写链表，一般不用动态分配，而是用静态数组来模拟。

手写链表的代码见题目：排队顺序

题解

#include 

using namespace std;

int arr[1000010];
int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> arr[i];
    }
    int head;
    cin >> head;
    cout << head;
    while (arr[head] != 0) {
        cout << " " << arr[head];
        head = arr[head];
    }
    return 0;
}

当然，除非必要，一般不手写链表，而是用系统提供的链表，例如C++ STL的list，Java LinkedList，Python的list。

链表在蓝桥杯等算法竞赛中不太常用，所以本章没有详细介绍。
 
（3）队列

队列是线性数据的一种使用方式，模拟现实世界的排队操作。例如排队购物，只能从队头离开队伍，新来的人只能排到队尾，不能插队。队列有一个出口和一个入口，出口是队头，入口是队尾。队列的编程实现，可以用数组，也可以用链表。

队列这种数据结构无所谓优缺点，只有适合不适合。例如宽度优先搜索BFS，就是基于队列的，用其他数据结构都不合适。

（4）栈

栈也是线性数据的一种使用方式，模拟现实世界的单出入口。例如一管泡腾片，先放进去的泡腾片后出来。栈的编程比队列更简单，同样可以用数组或链表实现。

栈有它的使用场合，例如递归使用栈来处理函数的自我调用过程。

1.3 二叉树简介

二叉树是一种高度组织性、高效率的数据结构。例如在一棵有n个节点的满二叉树上定位某个数据，只需走logn步，插入和删除某个数据也只需logn步。在二叉树的基础上发展出了很多高级数据结构和算法。大多数高级数据结构，例如树状数组、线段树、树链剖分、平衡树、动态树等，都是基于二叉树的。

2. 栈

栈（stack）是比队列更简单的数据结构，它的特点是“先进后出”。

队列有两个口，一个入口和一个出口。而栈只有唯一的一个口，既从这个口进入，又从这个口出来。所以如果自己写栈的代码，比队列的代码更简单。

2.1 手写栈

如果使用环境简单，最简单的手写栈代码用数组实现。

const int N = 300008;                        //定义栈的大小
struct mystack{
    int a[N];                                //存放栈元素，从a[0]开始
    int t = -1;                              //栈顶位置，初始栈为空，置初值为-1
    void push(int data){ a[++t] = data; }    //把元素data送入栈
    int top()   { return a[t]; }             //读栈顶元素，不弹出
    void pop()  { if(t>-1) t--;}             //弹出栈顶
    int size()  { return t+1;}               //栈内元素的数量
    int empty() { return t==-1 ? 1:0; }      //若栈为空返回1
};

使用栈时要注意不能超过栈的空间。上面第1行定义了栈的大小是N，栈内的元素数量不要超过它。

用下面的例子给出上述手写代码的应用。

例题：表达式括号匹配

题解：

合法的括号串例如“(())”、“()()()”，像“)(()”这样是非法的。合法括号组合的特点是：左括号先出现，右括号后出现；左括号和右括号一样多。

括号组合的合法检查是栈的经典应用。用一个栈存储所有的左括号。遍历字符串的每一个字符，处理流程是：
（1）若字符是 ‘(’，进栈。
（2）若字符是’)'，有两种情况：如果栈不空，说明有一个匹配的左括号，弹出这个左括号，然后继续读下一个字符；如果栈空了，说明没有与右括号匹配的左括号，字符串非法，输出NO，程序退出。
（3）读完所有字符后，如果栈为空，说明每个左括号有匹配的右括号，输出YES，否则输出NO。

C++代码

手写栈：

#include 
using namespace std;
const int N = 300008;                        //定义栈的大小
struct mystack{
    int a[N];                                //存放栈元素，从a[0]开始
    int t = -1;                              //栈顶位置，初始栈为空，置初值为-1
    void push(int data){ a[++t] = data; }    //把元素data送入栈
    int top()   { return a[t]; }         //读栈顶元素，不弹出
    void pop()  { if(t>-1) t--;     }        //弹出栈顶
    int size()  { return t+1;}            //栈内元素的数量
    int empty() {return t==-1 ? 1:0; }   //若栈为空返回1
}st;
int main(){
    char x;
	while(cin>>x){   //循环输入
	    if(x=='@') break;       //输入为@停止；
		if(x=='(') st.push(x);  //左括号入栈
		if(x==')'){             //遇到一个右括号
            if(st.empty()) {cout<<"NO";return 0;} //栈空，没有左括号与右括号匹配
            else st.pop();      //匹配到一个左括号，出栈
		}
	}
	if(st.empty()) cout<<"YES"; //栈为空，所有左括号已经匹配到右括号，输出yes
	else cout<<"NO";
	return 0;
}

STL：

#include 
using namespace std;
string str;
stack<char> ops;
int main()
{
    cin >> str;
    long res = 0;
    for (int i = 0; i < str.length(); i++) {
        char c = str[i];
        if (c == '(') {
            ops.push(c);
        }
        else if (c == ')') {
            if (!ops.empty()) {
                ops.pop();
            }
            else {
                cout << "NO";
                return 0;
            }
        }
    }
    if (!ops.empty()) {
        cout << "NO";
        return 0;
    }
    cout << "YES";
    return 0;
}

Java代码

import java.util.Scanner;
public class Main {
    static final int N = 300008;
    static class mystack {
        int[] a = new int[N];
        int t = -1;
        void push(int data) {  a[++t] = data;    }
        int top() {   return a[t];        }
        void pop(){   if(t > -1) t--;     }
        int size(){   return t + 1;       }
        boolean  empty() {   return t == -1 ? true : false; }
    }
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        mystack st = new mystack();
        String s = sc.next();
        for (int i = 0; i < s.length(); i++) {
            char x = s.charAt(i);
            if(x == '@') break;
            if(x == '(') st.push(x);
            if(x == ')') {
                if(st.empty()) {
                    System.out.println("NO");
                    return;
                }
                else st.pop();
            }
        }
        if(st.empty()) System.out.println("YES");
        else System.out.println("NO");
    }
}

Python代码

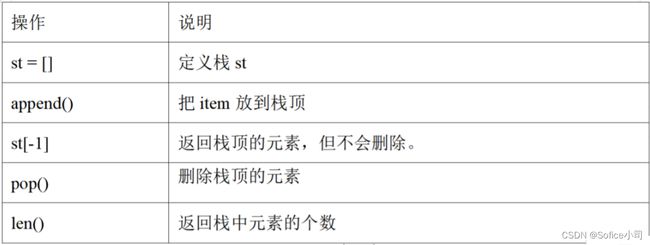
Python的手写栈用到了list。用list模拟栈有一个好处，不用担心栈空间不够大，因为list自动扩展空间。而且list的栈操作非常快，因为栈顶是list的末尾元素，栈只有一个出入口，只在list的末尾进行进栈和出栈操作，操作极为快捷。下面是list实现的栈功能。

下面是例题的Python代码，栈用list模拟。

st = []             #定义栈，用list实现
flag =  True        #判断左括号和右括号的数量是否一样多
s = input().strip()
for x in s:
    if x=='(':  st.append("(")    #进栈
    if x==")":
        if len(st)!=0:            #len()：栈的长度
            st.pop()              #出栈，也可以写成 del st[-1] ，st[-1]是栈顶
        else:                     #栈已空，没有匹配的左括号
           flag = False
           break
if len(st)==0 and flag:  print('YES')
else:                    print('NO')

2.2 C++STL栈

竞赛时一般不自己手写栈，而是用STL stack：https://wyqz.top/p/870124582.html#toc-heading-9。

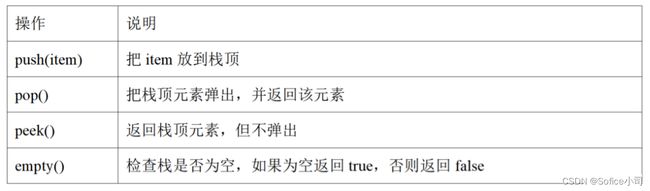
STL stack的主要操作见下表。

用下面的例题说明STLqueue的应用

例题：排列

题解：

把符合条件的一对称为一个“凹”。首先模拟检查“凹”，了解执行的过程。以“3 1 2 5”为例，其中的“凹”有：“3-1-2”和“3-1-2-5”；还有相邻的“3-1”、“1-2”、“2-5”。一共5个“凹”，总价值13。

像“3-1-2”和“3-1-2-5”这样的“凹”，需要检查连续3个以上的数字。

例如“3 1 2”，从“3”开始，下一个应该比“3”小，例如“1”，再后面的数字比“1”大，才能形成“凹”。

再例如“3-1-2-5”，前面的“3-1-2”已经是“凹”了，最后的“5”也会形成新的“凹”，条件是这个“5”必须比中间的“1-2”大才行。

总结上述过程是：先检查“3”；再检查“1”符合“凹”；再检查“2”，比前面的“1”大，符合“凹”；再检查“5”，比前面的“2”大，符合“凹”。

以上是检查一个“凹”的两头，还有一种是“嵌套”。一旦遇到比前面小的数字，那么以这个数字为头，可能形成新的“凹”。例如“6 4 2 8”，其中的“6-4-2-8”是“凹”，内部的“4-2-8”也是凹。如果学过递归、栈，就会发现这是嵌套，所以本题用栈来做很合适。

以“6 4 2 8”为例，用栈模拟找“凹”。当新的数比栈顶的数小，就进栈；如果比栈顶的数大，就出栈，此时找到了一个“凹”并计算价值。下图中的圆圈数字是数在数组中的下标位置，用于计算题目要求的价值。

图(1)：6进栈。
图(2)：4准备进栈，发现比栈顶的6小，说明可以形成凹，4进栈。
图(3)：2准备进栈，发现比栈顶的4小，说明可以形成凹，2进栈。
图(4)：8准备进栈，发现比栈顶的2大，这是一个凹“4-2-8”，对应下标“②–④”，弹出2，然后计算价值，j-i+1=④-②+1=3。
图(5)：8准备进栈，发现比栈顶的4大，这是一个凹“6-4-8”，对应下标“①–④”，弹出4，然后计算价值，j-i+1=④-①+1=4。
图(6)：8终于进栈了，数字也处理完了，结束。

在上述过程中，只计算了长度为3和3以上的凹，并没有计算题目中“（3）a[i]-a[j]之间不存在其他数字”的长度为2的凹，所以最后统一加上这种情况的价值(n-1)×2 = 6。

最后统计得“6 4 2 8”的总价值是3+4+6=13。

C++代码

#include 
using namespace std;
const int N = 300008;
int a[N];                 //这里a[]是题目的数字排列
int main(){
    int n;  cin>>n;
    for(int i = 1;i <= n;i++)  cin>>a[i];   //输入数列
    stack <int> st;                   //定义栈
    long long ans = 0;
    for(int i = 1;i <= n;i++){
        while(!st.empty() && a[st.top()] < a[i]){
            st.pop();
            if(!st.empty()){
                int last = st.top();
                ans += (i - last + 1);
            }
        }
        st.push(i);
    }
    ans += (n - 1) * 2;              //（3）a[i]-a[j]之间不存在其他数字的情况
    cout<<ans;
}

2.3 Java 栈

Java Stack https://docs.oracle.com/en/java/javase/14/docs/api/java.base/java/util/Stack.html

有以下操作。

例题 排列 的Java代码。

import java.util.Scanner;
import java.util.Stack;
public class Main {
    static final int N = 300008;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[] a = new int[N];
        for(int i = 1; i <= n; i++)  a[i] = sc.nextInt();        
        Stack<Integer> st = new Stack<>();
        long ans = 0;
        for(int i = 1; i <= n; i++) {
            while(!st.empty() && a[st.peek()] < a[i]) {
                st.pop();
                if(!st.empty()) {
                    int last = st.peek();
                    ans += (long)(i - last + 1);
                }
            }
            st.push(i);
        }
        ans += (n - 1) * 2;
        System.out.println(ans);
    }
}

2.4 Python栈

python的栈可以用以下三种方法实现：（1）list；（2）deque；（3）LifoQueue。比较它们的运行速度，list和deque一样快，而LifoQueue慢得多，建议使用list。前面已经介绍了用list实现栈的方法。

下面是例题 排列 的代码。

n = int(input())
a = [int(x) for x in input().split()]
st = []                                       #定义栈，用list实现
ans = 0
for i in range(n):
    while len(st) != 0 and a[st[-1]] < a[i]:  #st[-1]是栈顶
        st.pop()                              #弹出栈顶
        if len(st) != 0:
            last = st[-1]                     #读栈顶
            ans += (i - last + 1)
    st.append(i)                              #进栈
ans += (n - 1) * 2
print(ans)

3 习题

表达式括号匹配

表达式求值

小鱼的数字游戏

后缀表达式

【模板】栈

栈