【LeetCode】链式二叉树OJ题---C语言版
链式二叉树OJ题
- 一、单值二叉树
-
- (1)题目描述:
- (2)思路表述:
- (3)代码实现:
- 二、二叉树最大深度
-
- (1)题目描述:
- (2)思路表述:
- (3)代码实现:
- 三、检查两颗树是否相同
-
- (1)题目描述:
- (2)思路表述:
- (3)代码实现:
- 四、二叉树的前序遍历
-
- (1)题目描述:
- (2)思路表述:
- (3)代码实现:
- 五、翻转二叉树
-
- (1)题目描述:
- (2)思路表述:
- (3)代码实现:
- 六、另一颗树的子树
-
- (1)题目描述:
- (2)思路表述:
- (3)代码实现:
- 七、二叉树的构建及遍历
-
- (1)题目描述:
- (2)思路表述:
- (3)代码实现:
一、单值二叉树
(1)题目描述:
(2)思路表述:
- 如果传回来是空节点,那么就返回真。
- 如果传过来只有一个节点,那么我们也返回真
- 首先我们应该先判断不相等的,因为相等的他肯定要递归嘛(最值得注意的是,你得先判断这个左/右子树,它存在不存在!只有左/右子树存在了,才能判断左/右子树中的值跟它的根节点是否相等。如果左子树不存在,我们都不需要判断它!如果左子树不存在,我们就直接访问空了,这样会报错的。)
- 如果以上的三种情况都不符合的话,我们就继续递归往下走。
(3)代码实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
bool isUnivalTree(struct TreeNode* root)
{
//1.如果传回来是空节点,那么就返回真。
if(root==NULL)
{
return true;
}
//2.如果传过来只有一个节点,那么我们也返回真
if(root->left==NULL&&root->right==NULL)
{
return true;
}
//3.首先我们应该先判断不相等的,因为相等的他肯定要递归嘛
//最值得注意的是,你得先判断这个左/右子树,它存在不存在!只有左/右子树存在了,才能判断左/右子树中的值跟它的根节点是否相等。如果左子树不存在,我们都不需要判断它!如果左子树不存在,我们就直接访问空了,这样会报错的。
if(root->left&&root->left->val!=root->val)
{
return false;
}
else if(root->right&&root->right->val!=root->val)
{
return false;
}
//4.如果以上的三种情况都不符合的话,我们就继续递归往下走。
return isUnivalTree(root->left)&&isUnivalTree(root->right);
}
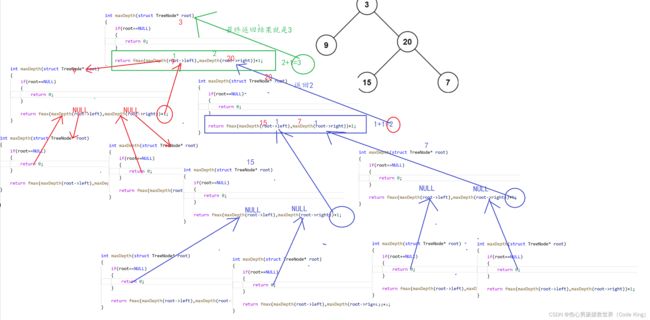
二、二叉树最大深度
(1)题目描述:
(2)思路表述:
从根开始分别遍历左子树和右子树,取最大的就是整个树的最大深度
(3)代码实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
int maxDepth(struct TreeNode* root)
{
if(root==NULL)
{
return 0;
}
return fmax(maxDepth(root->left),maxDepth(root->right))+1;
}
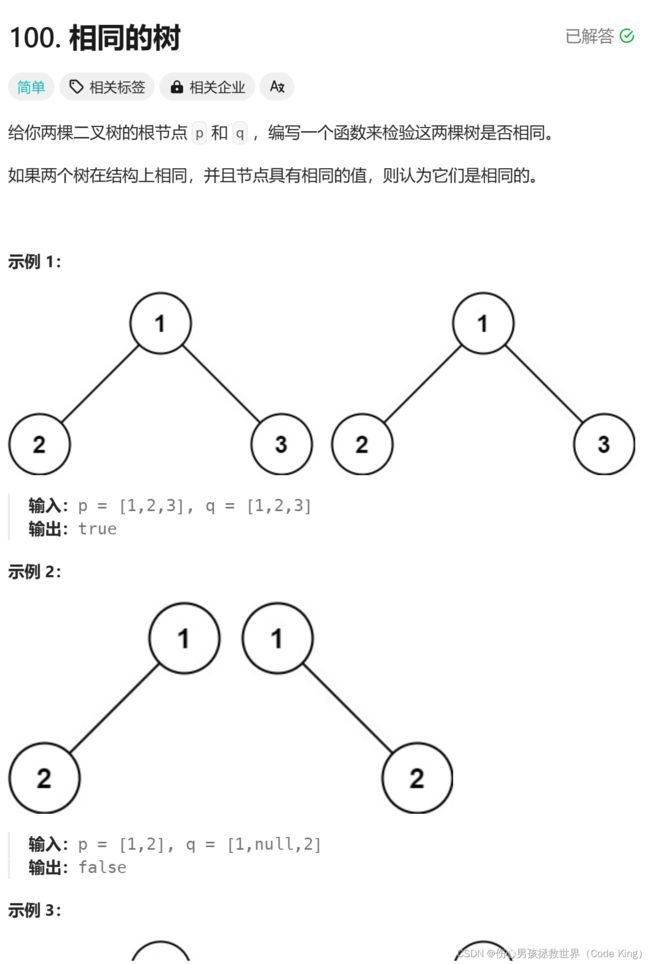
三、检查两颗树是否相同
(1)题目描述:
(2)思路表述:
1.如果两个二叉树都为空,则两个二叉树相同。
2.如果两个二叉树中有且只有一个为空,则两个二叉树一定不相同。
3.如果两个二叉树都不为空,那么首先判断它们的根节点的值是否相同,若不相同则两个二叉树一定不同,若相同,再分别判断两个二叉树的左子树是否相同以及右子树是否相同。这是一个递归的过程,因此可以使用深度优先搜索,递归地判断两个二叉树是否相同。
(3)代码实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
//两个都为空
if(p==NULL&&q==NULL)
{
return true;
}
//一个为空,一个不为空
if(p==NULL||q==NULL)//if((p==NULL&&q!=NULL)||(p!=NULL&&q==NULL))
{
return false;
}
//两个都不为空
//1.先判断不相等
if(p->val!=q->val)
{
return false;
}
//2.如果相等
return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}
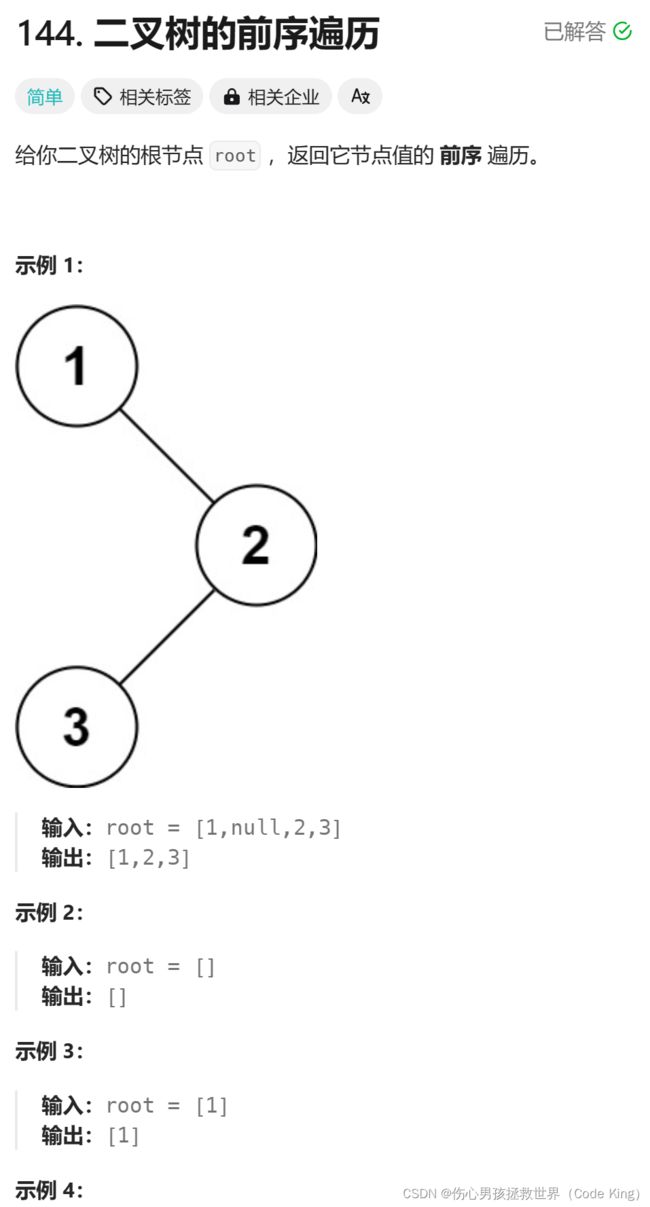
四、二叉树的前序遍历
(1)题目描述:
点击链接
(2)思路表述:
- 创建一个刚好满足所有储存树的结点的数组空间大小
- 以前序的方式把树中的结点依次放入数组中
(3)代码实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int TreeSize(struct TreeNode* root)
{
return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
}
void Prevorder(struct TreeNode* root,int* arr,int* i)
{
if(root==NULL)
{
return;
}
arr[(*i)++]=root->val;
Prevorder(root->left,arr,i);
Prevorder(root->right,arr,i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
//1.创建一个刚好满足所有储存树的结点的数组空间大小
int n=TreeSize(root);
int* arr=(int*)malloc(sizeof(int)*n);
int i=0;
//2.以前序的方式把树中的结点依次放入数组中
Prevorder(root,arr,&i);
*returnSize=n;
return arr;
}
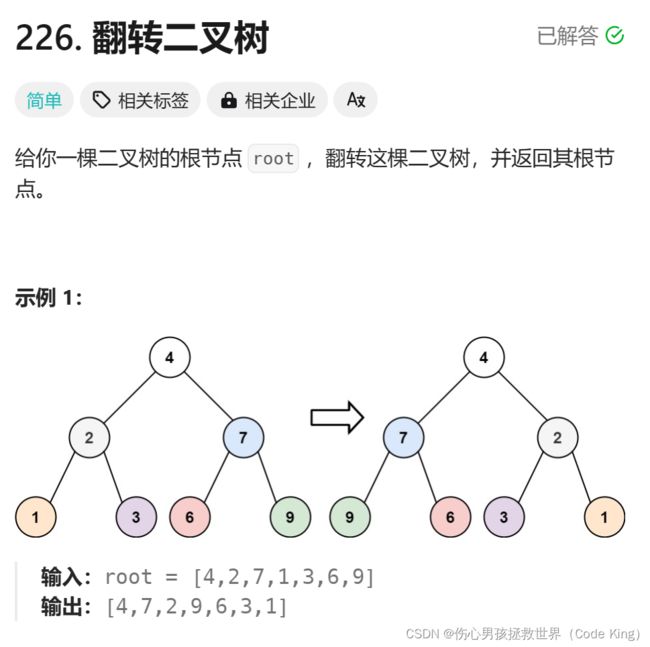
五、翻转二叉树
(1)题目描述:
(2)思路表述:
- 我们从根节点开始,递归地对树进行遍历,并从叶子节点先开始翻转
- 一直遍历到树的的叶子节点
- 如果当前遍历到的节点 root 的左右两棵子树都已经翻转,那么我们只需要交换两棵子树的位置,即可完成以 root 为根节点的整棵子树的翻转。
不理解的时候:就画递归展开图就行!
(3)代码实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
//不理解的时候:就画递归展开图就行!
struct TreeNode* invertTree(struct TreeNode* root)
{
if(root==NULL)
{
return NULL;
}
//我们从根节点开始,递归地对树进行遍历,并从叶子节点先开始翻转
struct TreeNode* left=invertTree(root->left);//一直遍历到树的的叶子节点
struct TreeNode* right=invertTree(root->right);
root->left=right;
root->right=left;
//如果当前遍历到的节点 root 的左右两棵子树都已经翻转,那么我们只需要交换两棵子树的位置,即可完成以 root 为根节点的整棵子树的翻转。
return root;
}
六、另一颗树的子树
(1)题目描述:
(2)思路表述:
-
如果root为NULL,我们就返回空:NULL
-
首先我们先判断刚开始的root和subroot的根相不相等?如果相等,然后再判断是否是相同的树
-
如果刚开始root->val!=subroot->val,不要着急!继续遍历root的左,右子树
(3)代码实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
//两个都为空
if(p==NULL&&q==NULL)
{
return true;
}
//一个为空,一个不为空
if(p==NULL||q==NULL)//if((p==NULL&&q!=NULL)||(p!=NULL&&q==NULL))
{
return false;
}
//两个都不为空
//1.先判断不相等
if(p->val!=q->val)
{
return false;
}
//2.如果相等
return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
if(root==NULL)
{
return false;
}
//2.首先我们先判断刚开始的root和subroot的根相不相等?如果相等,然后再判断是否是相同的树
if(root->val==subRoot->val)
{
if(isSameTree(root,subRoot))
{
return true;
}
//return isSameTree(root,subRoot);不能这样写,因为如果这样写的话,可能root的下面可能有子树和传过来的subroot是相同的树,
//但是你没有判断,直接return返回了,这样就有所欠缺!
}
//3.如果刚开始root->val!=subroot->val,不要着急!继续遍历root的左,右子树
return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}
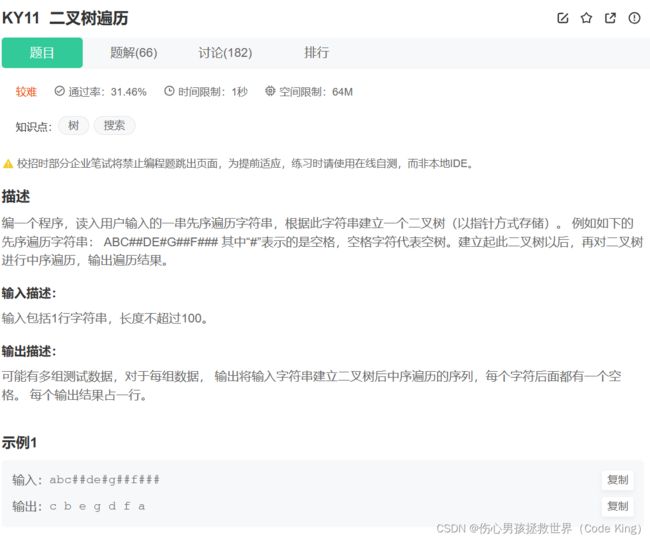
七、二叉树的构建及遍历
(1)题目描述:
(2)思路表述:
- 读入字符串
- 创建二叉树
- 中序打印二叉树
(3)代码实现:
#include 好了,今天的分享就到这里了
如果对你有帮助,记得点赞+关注哦!
我的主页还有其他文章,欢迎学习指点。关注我,让我们一起学习,一起成长吧!