Hypergraph Neural Networks笔记
1 Title
Hypergraph Neural Networks(Yifan Fengy, Haoxuan Youz, Zizhao Zhangz, Rongrong Jiy
, Yue Gao)【AAAI 2019】
2 Conclusion
This paper propose a hypergraph neural networks (HGNN) framework for data representation learning, which can encode higher-order data correlation in hypergraph structures. In this method, a hyper-edge convolution operation is designed to deal with the data correlation in the process of representation learning, so that the traditional hypergraph learning process can be effectively carried out by using the hyper-edge convolution operation. HGNN performs well on multiple modalities.
3 Good Sentence
1、On the contrary, a hypergraph is easy to be expanded for multi-modal and heterogeneous data representation using its flexible hyperedges. For example, a hypergraph can jointly employ multi-modal data for hypergraph generation by combining the adjacency matrix. However, traditional hypergraph learning methods (Zhou, Huang, and Scholkopf 2007) suffer from their high computation complexity and storage cost, which limits the wide application
of hypergraph learning methods.(The shortcomings and advantages of traditional hypergraph learning methods)
2、the expansive computation of Laplacian Eigen vectors is excluded and only matrix powers, additions and multiplications are included, which brings further improvement in computation complexity.(The improvement of Laplacian Eigen vectors)
3、HGNN is a more general framework which is able to handle the complex
and high-order correlations through the hypergraph structure for representation learning.Experimental results and comparisons withthe state-of-the-art methods demonstrate the better performance of the proposed HGNN model.(The advantages of the HGNN methods)
摘要
本文提出了一种用于数据表示学习的超图神经网络(hypergraph neural networks,HGNN)框架,它可以将高阶数据相关性编码在超图结构中。在这种方法中,设计了一种超边卷积运算来处理表示学习过程中的数据相关性,这样,传统的超图学习过程可以有效地使用超边卷积运算来进行。HGNN在多模态上表现良好
介绍
现实世界的关系比成对链接(图)复杂的多,研究更好、更通用的数据结构模型来学习表示就非常重要和迫切。本文提出了一种基于超图结构的超图神经网络(HGNN)模型框架。
本文的主要贡献:1、提出HGNN,HGNN能够通过其超图结构来制定复杂和高阶的数据相关性,并且还可以使用超边卷积运算。GCN可以看作是HGNN的一个特例,简单图中的边可以看作是连接两个顶点的二阶超边。2、通过实验,HGNN在处理多模态数据时也有较好的性能
HGNN
符号:超图G,顶点V,超边E,权重W,关联矩阵H,顶点阶数d(v),超边阶数![]() ,阶数的矩阵形式是
,阶数的矩阵形式是![]() 。
。
对于超图上的节点分类问题,超图结构上的节点标签应该是光滑的。这种任务可以被公式化为正则化框架 ((Zhou, Huang, and Scholkopf 2007)![]() ,其中,
,其中,![]() 是超图上的正则化。
是超图上的正则化。![]() 是监督经验损失。
是监督经验损失。![]() 是一个分类函数。直接算
是一个分类函数。直接算![]() 比较麻烦,但是用拉普拉斯算子的话
比较麻烦,但是用拉普拉斯算子的话![]() ,L就是半正定的超图拉普拉斯算子。
,L就是半正定的超图拉普拉斯算子。
超图上的谱(Spectral)卷积:
给定一个n阶超图G=(V,E,W),因为超图拉普拉算子L是半正定的n阶矩阵,所以可以分解成![]() ,这样就能得到正交特征向量
,这样就能得到正交特征向量![]() 和一个包含对应的非负特征值的对角矩阵
和一个包含对应的非负特征值的对角矩阵![]() =
=![]() ,然后在超图中对信号x进行傅里叶变化,定义为
,然后在超图中对信号x进行傅里叶变化,定义为![]() ,其中,特征向量被视为傅里叶基,特征值被视为频率。
,其中,特征向量被视为傅里叶基,特征值被视为频率。
其中![]() 表示逐元素Hadamard乘,
表示逐元素Hadamard乘,![]() 是傅里叶系数的函数,为了解决傅里叶变换计算代价大的问题,可以遵循(Defferrard,Bresson和Vandergheynst 2016)用K阶多项式参数化
是傅里叶系数的函数,为了解决傅里叶变换计算代价大的问题,可以遵循(Defferrard,Bresson和Vandergheynst 2016)用K阶多项式参数化![]() ,并用截断切比雪夫展开成这样的公式:
,并用截断切比雪夫展开成这样的公式: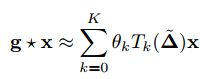 ,其中,
,其中,![]() 是具有缩放拉普拉斯算子的k阶切比雪夫多项式。
是具有缩放拉普拉斯算子的k阶切比雪夫多项式。
由于在这个公式中,超图中的拉普拉斯算子已经能够很好地表示节点之间的高阶相关性,那么可以进一步让K = 1来限制卷积运算的阶数
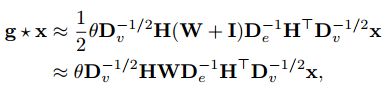 当有超图信号X:n个节点和
当有超图信号X:n个节点和![]() 维特征时,超边卷积可以表示为
维特征时,超边卷积可以表示为![]() ,其中过滤器θ是一个可学习的参数,应用于超图中的节点以提取特征,最后得到的Y可以用来分类
,其中过滤器θ是一个可学习的参数,应用于超图中的节点以提取特征,最后得到的Y可以用来分类
用以下公式构建超边卷积层
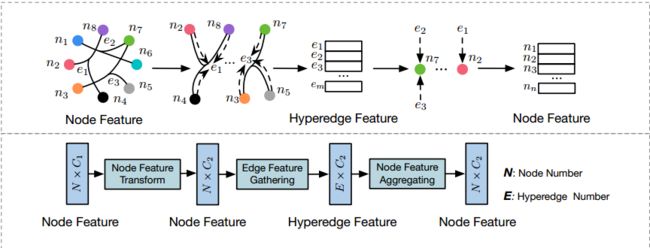
![]() ,其中σ是非线性激活函数,X是超图信号,HGNN模型基于超图上的谱卷积,如上面的图所示,HGNN层可以执行节点-超边-节点变换,这可以使用超图结构更好地细化特征。
,其中σ是非线性激活函数,X是超图信号,HGNN模型基于超图上的谱卷积,如上面的图所示,HGNN层可以执行节点-超边-节点变换,这可以使用超图结构更好地细化特征。
首先对初始节点特征X进行可学习滤波矩阵Θ处理,提取![]() 维特征,然后根据超边缘对节点特征进行聚集,形成超边特征R,最后将它们相关的超边特征聚合得到输出节点特征,有效地提取超图上的高阶相关性。
维特征,然后根据超边缘对节点特征进行聚集,形成超边特征R,最后将它们相关的超边特征聚合得到输出节点特征,有效地提取超图上的高阶相关性。
实验:
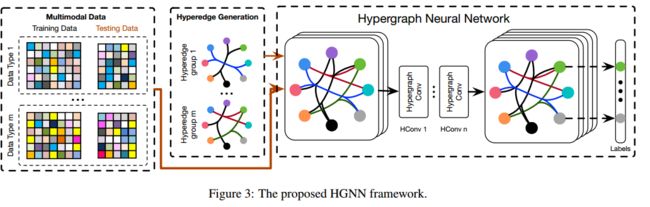
 首先将数据集分为训练数据和测试数据,然后按照上述方法构造超图,生成关联矩阵H和对应的De。实验构造了如图所示的模型,HGNN模型为2层,使用softmax函数生成预测标签,用交叉熵损失反向传播更新参数Θ,通过预测测试数据的标签评估性能,当存在多模态信息时,通过构造超边组将多模态信息合并,然后将多个超边融合在一起,对数据上的复杂关系进行建模。
首先将数据集分为训练数据和测试数据,然后按照上述方法构造超图,生成关联矩阵H和对应的De。实验构造了如图所示的模型,HGNN模型为2层,使用softmax函数生成预测标签,用交叉熵损失反向传播更新参数Θ,通过预测测试数据的标签评估性能,当存在多模态信息时,通过构造超边组将多模态信息合并,然后将多个超边融合在一起,对数据上的复杂关系进行建模。
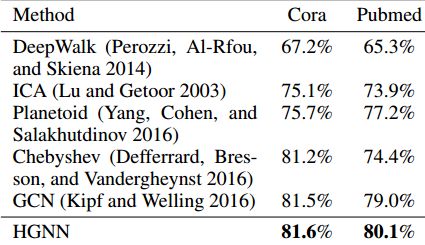
节点分类任务上的具体设置:隐藏层的特征维度设置为16,并使用dropout来避免过拟合,丢弃率p = 0:5。非线性激活函数选择relu,训练选择adam优化器来最小化交叉熵损失函数,学习率设定为0.001。将HGNN与当时的主流算法坐了比较。