Improving Hypergraph Attention and Hypergraph Convolution Networks笔记

1.Title

        Improving Hypergraph Attention and Hypergraph Convolution Networks(Mustafa Mohammadi Garasuie、Mahmood Shabankhah、Ali Kamandi) 【IEEE 2020】

2.conclusion

          Some problems require that we consider a more general relationship which involve not only two nodes but rather a group of nodes. This is the approach adopted in Hypergraph Convolution and Hypergraph Attention Networks (HGAT). This paper first propose to incorporate a weight matrix into these networks which, as our experimentations show, can improve the performance of the models in question. The other novelty in our work is the introduction of self-loops in the graphs which again leads to slight improvements in the accuracy of our architecture(named iHGAN).

3.Good Sentences

        1、 In simple terms, a hypergraph is a special type of graph where more than two vertices may be connected through what is called a hyper-edge. Successful attempts has been made to adopt this approach to tackle classical machine learning problems such as classification problems . Our main goal in this paper is to use hypergraph convolution networks to boost the accuracy of some known GCN models which deal with unstructured data.(The works this paper has done)

        2、The main problem in a hypergraph is that how we can propagate appropriate information in vertices between each other by having hyperedges compared with graphs. As mentioned in the previous sections, the relation between vertices in hypergraphs is hyperedges. They can connect more than two vertices by one hyperedge. Thus, the innate transition probability between vertices is not clear in hypergraphs compared with graphs. (The problems in hypergraph and then how to solve them.)

        3、 One solution to tackle this none-learnable matrix is to add parallel MLP with a learnable matrix, as known module, to compel our architecture to learn some weights using incident matrix H. In this technique, each vertex cooperates to the architecture in a probabilistic way in our all attention mechanism(our extra-matrix is as a hyper-parameter in learning steps)（the schematic of this method proposed by this paper）

        4、A major challenge, however, in these situations is that most often input data and their interrelationships are of an inhomogeneous type which makes it impossible to properly exploit hypergraphs. One possible solution is to somehow map the objects and their relationships into a latent space where conventional graph approaches are feasible.（The frame of problem in real world and the method to solve）

---

超图卷积可以定义为以下方程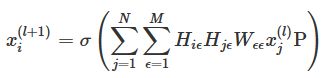：，其矩阵形式：其中，是第l层上的节点特征，H是关联矩阵，P是层l和层（l+1）之间的架构权重（the weight of framework）

         在各种各样的神经网络架构中，层应该堆叠，所以Eq。 (5) 在很多情况下也应该堆叠。为了避免梯度消失，一个任务是规范化超图卷积公式。两种常见的规范化是对称和行规范化

        其中，D代表阶数，的特征值不会大于1。两个规范化之间的主要区别是行规范化中的传播是定向的和非对称的。

---

在超图中，一个特征与一组由超边连接的顶点之间的联系并不十分清楚。此外，顶点之间的转移概率在超边之间并不明显。有几种技术可以定义用于在超边中的顶点之间变换数据的转移概率

---

        由关联矩阵H获得的注意力机制是不可学习的。解决这个不可学习矩阵的一个解决方案是添加具有可学习矩阵的并行MLP（多层感知器），以迫使架构使用关联矩阵H来学习一些权重。在这种技术中，每个顶点在所有的注意力机制中以概率的方式与架构合作（额外矩阵作为学习步骤中的超参数）。也就是说，通过使用一个特定的矩阵，在构建块（并行MLP）中相乘，来计算架构中超边合作的各个部分【we will use a particular matrix to multiply in our building blocks(our parallel MLP) to calculate a various portion of hyperedges co-operation in the architecture】，但是图的顶点和超边集来自同一个齐次域的时候才能使用这种方法

---

生成超图的几个方法：

1、KNN（K-近邻方法）

2、基于图中顶点之间的共同特征创建超图

3、随机游走法

还有一些其他方法可以从给定的图形创建超图，例如归一化切割等，但是NPhard问题。

当超边和顶点具有可比性时，我们可以使用 [P. Velickovic, G. Cucurull, A. Casanova, A. Romero, P. Lio and Y. Bengio, Graph attention networks, 2017.] 创建注意力机制。注意力操作和评分可以如下：其中，是的邻域。注意力机制用于提高嵌入层中的中间注意力。因此，毫无疑问，这种架构可用于端到端学习。

图卷积和超图卷积之间存在合理的关系。设 A ∈为邻接矩阵。与超边相比，每条边只能连接两个顶点。设 B ═ 2I 为顶点度矩阵，并假设所有超边具有相同的权重（例如，W = I）。超图卷积定义如下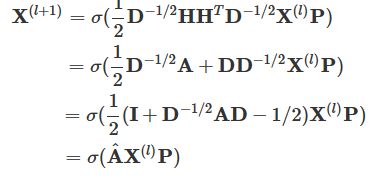。其中，应该是-1/2，写错了。

---

本文iHGAN与HGAN相比所做的主要改进是在架构中增加的自循环。此外，超边权重也可以添加到此体系结构中。从给定图生成超图的机制是，对于每个顶点，其所有相邻顶点和所选顶点都应该位于相同的超边中。为了更详细地描述这个概念，其表述如下：