DS-追星(Dijkstra求单源最短路)
Description
城市总共有N座。yintama是右京女神的狂热粉,当他得知右京女神将要在城市N举办演唱会的时候,马上开始准备动身前往城市N。原本他可以直接乘飞机直达城市N,然而贫穷使他屈服,他必须选择总花费最少的那条路径。
设总共有N座城市(2<=N<=1000),城市编号分别为1,2,3……N。M条航线(1<=M<=2000),每条航线连接两座城市,相互可以到达(无向的)。
yintama目前在身在城市1,求最后yintama参加右京女神演唱会所需要的最少花费。(PS:重边考虑一下?)
Input
有多组输入。
第一行输入一个N、M,代表城市的总数,以及航线的总数。
接下来M行,每行输入三个数字u v w,代表城市u、v之间存在航线,机票花费为w。
Output
每行输出一个数,代表yintama参加右京女神演唱会所需的最少花费。
Sample
#0
Input
5 5 1 2 20 2 3 30 3 4 20 4 5 20 1 5 100
Output
90
Dijkstra原理:
以起点 A 通往前一个点 B 的最短路径+前一个点 B 到下一个点 C 的路径与 现有的A通到C的路径距离相比较求一个最短的路劲。(这里可能不是太理解,请往下看)
首先先知道一个算法里面一个重要的东西 dis[] 数组,他的意思是起点到终点的距离
设起点为 0
dis[0],起点 0 到 0 的最短距离
dis[1],起点 0 到 1 的最短距离
dis[2],起点 0 到 2 的最短距离
这里与开头说的联系;
假设 0 到 2 存在一条路距离为10 ,0 到 1 存在一条路距离为2 ,1到2存在一条路距离为3

dis[0]=0
dis[1]=2
然后最开始以 2 为前一个出发点,那到达 2 的最短距离已知的是不是10,dis[2]=10
然后 1 为中转点到达 2 的时候,到达2的距离是不是 到达 1 的距离+ 1 到 2的距离dis[1]+1->2=5
此时dis[1]+3
样例(自己出的样例跑一遍)
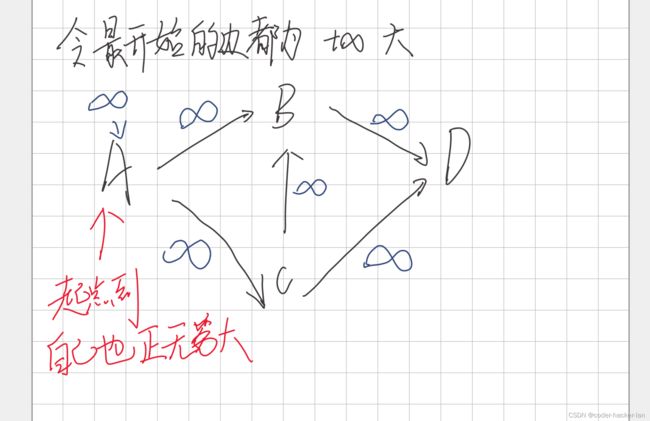
dis[A]=无穷大 dis[B]=无穷大 dis[C]=无穷大,dis[D]=无穷大
本题设置A为起点
图如下: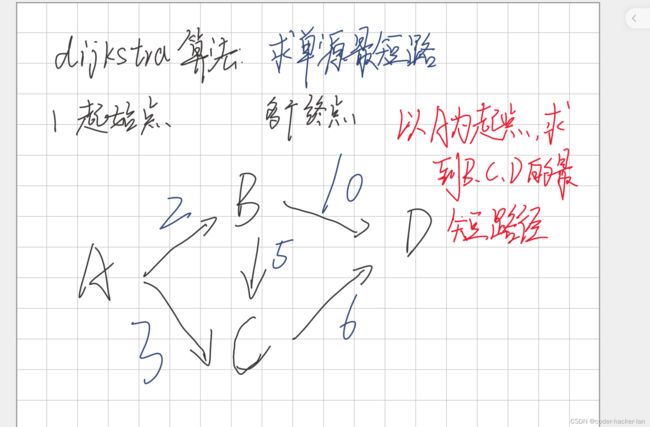
令dis[]都为无穷大
然后dis[]数组中dis[A]是最小的,且没有被作为中转点走过,所以设A为中转点,然后遍历A可以到达的边。这里可以理解为A-A(中转点)-目标点
A可以到达B,C两点,且A到B,C的距离小于无穷大,所以更新起点A到B,C的最短距离为
dis[B]=2,dis[C]=3
✔的意思是这个点已经被作为中转点走过了
然后找未被作为起始点且起点到他的距离最短,找到B,因为dis[B]=2,dis[C]=3,dis[A]=0但是A已经作为中转点走过了。
B可以到达D点,
起初dis[D]=无穷大,意思为A到D的最短距离为无穷
现在D的路径有从B到D,他的距离为起点A到达B的最短距离+BD路径的距离
dis[B]+BD=12<无穷大
所以dis[D]=12
然后继续重复步骤
此时没有被走过的点是C,D.dis[C]=3,dis[D]=12 1.C可以到达B
1.C可以到达B
起点A到C的最短距离+CB为B的新一条路距离>dis[B]的前一个路径,即起点A到B的最短路径
dis[C]+CB=8 > dis[B]=2
所以不用更新dis[B]
2.C可以到达D
起点A到D的最短距离+CD为D的新一条路距离
所以需要更新起点A到D的最短距离dis[D]=9
最后以D为中转点走,即A到D的最短路径 出发去别的点,但是已经没有D可以到达的点了,所以就结束了
最后得到起点A到别的点的距离
dis[A]=0
dis[B]=2
dis[C]=3
dis[D]=9
代码实现
#include
#include
#include
using namespace std;
const int maxn = 2e3 + 10;
int n, m;
int dis[maxn];///起点到终点距离的数组
int vis[maxn];///判断这个点是否有被作为中转点走过的数组
int p[maxn][maxn];///用邻接矩阵判断i到j是否存在边
void irit()//初始化,dis数组设置为无穷大,vis数组设置为都没有被访问过
{
for (int i = 0; i <= n; i++)
{
vis[i] = 0;
dis[i] = 0x3f3f3f;
}
}
void dijkstra()
{
dis[1] = 0;///本题起点是0,所以0到0距离为0
for (int i = 1; i <= n; i++)///然后本题其实最多只用循环点的个数n次就够了,每次找一个中转点
{
int minm = 0x3f3f3;
int j = 0;
for (int k = 1; k <= n; k++)///遍历所有dis[],找最小距离的点且没有被作为中转点走过的点
{
///vis[k]=0即没有被作为中转点,dis[k]即比较dis距离找距离最小的点
if (!vis[k] && dis[k] < minm)
{
j = k;//找距离最小的点
minm = dis[k];//更新最短距离
}
}
vis[j] = 1;///将这个点设置为已经被中转过了
for (int k = 1; k <= n; k++)///找这个中转点可以到达的k点,如果起点到K的距离小于通过中转点到K的距离就不用更新
{
///如果起点到K的距离大于通过中转点到K的距离就需要更新
///p[j][k],j到k是否存在边
if (p[j][k] != 0 && dis[j] + p[j][k] < dis[k])
{
dis[k] = dis[j] + p[j][k];
}
}
}
}
int main()
{
cin >> n >> m;
irit();
memset(p, 0, sizeof(p));//邻接矩阵初始化都没有边
for (int i = 0; i < m; i++)
{
int a, b, c;
cin >> a >> b >> c;
if (p[a][b] != 0)///构建邻接矩阵
{
///这个措施是不知道题目要求的重边什么意思
///担心比如A-B存在一条路距离为10
/// 但是又有一条路是A-B的距离为5,所以取最小的边
p[a][b] = min(p[a][b], c);
p[b][a] = min(p[b][a], c);
}
else
{
p[a][b] = c;
p[b][a] = c;
}
}
dijkstra();///dijkstra算法的实现
cout << dis[n] << endl;///输出起点到n点的最短距离
return 0;
}