分治-归并算法——LCR 170. 交易逆序对的总数
文章目录
- 0. 归并排序
- 1. 题目
- 2. 算法原理
- 3. 代码实现
0. 归并排序
归并排序是典型的分治,将数组分成若干个子数组,数组两两比较,不是很清楚的,可以查看此篇文章——数据结构——七大排序
这里以力扣912. 排序数组为例:
class Solution {
vector<int> tmp;
public:
vector<int> sortArray(vector<int>& nums)
{
tmp.resize(nums.size());
mergeSort(nums, 0, nums.size()-1);
return nums;
}
void mergeSort(vector<int>& nums, int left, int right)
{
if(left >= right) return;
int mid = left + (right-left)/2;
//[left,mid] [mid+1,right]
mergeSort(nums,left,mid);
mergeSort(nums,mid+1,right);
//合并
int i = 0,
cur1 = left,
cur2 = mid+1;
while(cur1 <= mid && cur2 <= right)
tmp[i++] = nums[cur1] <= nums[cur2] ? nums[cur1++] : nums[cur2++];
//检查没有遍历完的数组
while(cur1 <= mid) tmp[i++] = nums[cur1++];
while(cur2 <= right) tmp[i++] = nums[cur2++];
//还原到原数组
for(int i = left; i <= right; i++) nums[i] = tmp[i-left];
}
};
1. 题目
题目链接:LCR 170. 交易逆序对的总数
在股票交易中,如果前一天的股价高于后一天的股价,则可以认为存在一个「交易逆序对」。请设计一个程序,输入一段时间内的股票交易记录 record,返回其中存在的「交易逆序对」总数。
示例 1:
输入:record = [9, 7, 5, 4, 6]
输出:8
解释:交易中的逆序对为 (9, 7), (9, 5), (9, 4), (9, 6), (7, 5), (7, 4), (7, 6), (5, 4)。
限制:
0 <= record.length <= 50000
2. 算法原理
逆序对的意思就是,从数组中挑2个数,前面的数大于后面的数 且 前一个数的下标小于后一个数的下标,然后查看有几对
解法一:暴力枚举
固定一个数,找后面的区间,两层for循环即可,但是这个题目的等级是困难,对于力扣的题目等级划分,简单题基本可采用暴力解法,但是在中等及困难这两个等级,暴力解法大部分都是行不通的。
解法一:归并
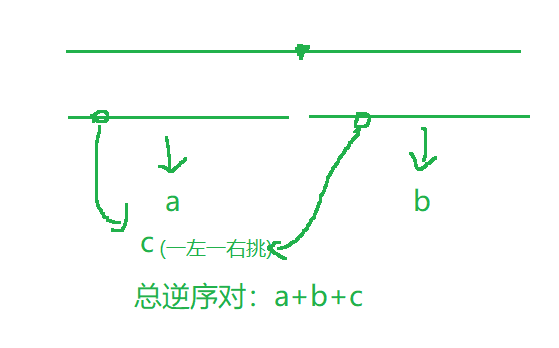
如果要求整个数组的逆序对,我们可以将数组分为两部分,先求左边区域的逆序对,再求右边区域的逆序对,然后左边选一个、右边选一个,看看这样有多少个逆序对,这个的本质其实还是属于暴力枚举
我们在此想法是再优化一下,即当左边区域挑选完毕之后,对左区域排序;右边区域挑选完毕之后,对右区域排序,然后再挑选,一左一右挑选完毕之后,再排一下序,这个过程就和归并排序的过程一样了。
为什么归并会快(升序为例)?
我们固定一个数,要找出有多少个数比这个数大,在上图,我们看对于
cur2,在左区间有多少个数比这个数大,这样就和归并排序完美契合,分3种情况:
nums[cur1] <= nums[cur2]–>cur1++(<和=情况操作一样)nums[cur1] > nums[cur2],此时cur1后面的元素全部大于nums[cur2],然后就能直接统计出一大堆ret += mid - cur1 + 1,cur2++所以,这个时间复杂度就和归并排序的时间复杂度一模一样O(N*logN)
细节问题:
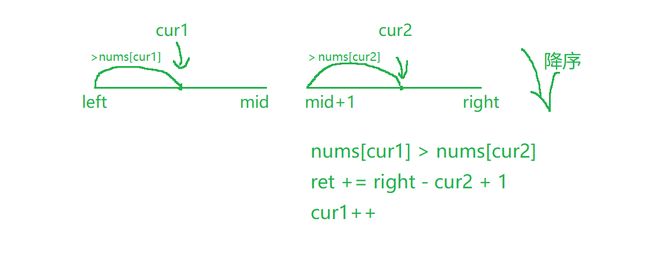
刚刚是以升序为例,如果采用降序,即找出该数之后,有多少个小于该数的元素
3. 代码实现
升序:
class Solution {
int tmp[50001];
public:
int reversePairs(vector<int>& record)
{
return mergeSort(record,0,record.size()-1);
}
int mergeSort(vector<int>& nums, int left, int right)
{
if(left >= right) return 0;
int ret = 0;
int mid = (left + right) >> 1;
//[left,mid] [mid+1,right]
//左边逆序对个数 排序
//右边逆序对个数 排序
ret += mergeSort(nums,left,mid);
ret += mergeSort(nums,mid+1,right);
//一左一右个数
int cur1 = left,
cur2 = mid+1,
i = 0;
while(cur1 <= mid && cur2 <= right)
{
if(nums[cur1] <= nums[cur2]) tmp[i++] = nums[cur1++];
else
{
ret += mid - cur1 + 1;
tmp[i++] = nums[cur2++];
}
}
//排序
while(cur1 <= mid) tmp[i++] = nums[cur1++];
while(cur2 <= right) tmp[i++] = nums[cur2++];
for(int i = left; i <= right; i++) nums[i] = tmp[i-left];
return ret;
}
};
降序:
class Solution {
int tmp[50001];
public:
int reversePairs(vector<int>& record)
{
return mergeSort(record,0,record.size()-1);
}
int mergeSort(vector<int>& nums, int left, int right)
{
if(left >= right) return 0;
int ret = 0;
int mid = (left + right) >> 1;
//[left,mid] [mid+1,right]
//左边逆序对个数 排序
//右边逆序对个数 排序
ret += mergeSort(nums,left,mid);
ret += mergeSort(nums,mid+1,right);
//一左一右个数
int cur1 = left,
cur2 = mid+1,
i = 0;
while(cur1 <= mid && cur2 <= right)
{
if(nums[cur1] <= nums[cur2]) tmp[i++] = nums[cur2++];
else
{
ret += right - cur2 + 1;
tmp[i++] = nums[cur1++];
}
}
//排序
while(cur1 <= mid) tmp[i++] = nums[cur1++];
while(cur2 <= right) tmp[i++] = nums[cur2++];
for(int i = left; i <= right; i++) nums[i] = tmp[i-left];
return ret;
}
};
运行结果: