组合总和II（回溯、去重）

40. 组合总和 II - 力扣（LeetCode）

题目描述

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

注意：解集不能包含重复的组合。 

样例输入

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]

提示:

• 1 <= candidates.length <= 100
• 1 <= candidates[i] <= 50
• 1 <= target <= 30

题解

本题与该题组合总和（回溯）-CSDN博客的区别在于，candidates 候选集合中有重复的元素，然而解集中要求不能包含重复的组合，因此在求解时要对解集进行去重。

举个例子，如下图，当candidates = [10,1,2,7,6,1,5]，target=8时，显然[1,7]是一个解集，但是candidates 存在两个元素1，也就是图中指针a和指针c指向的元素，如果我们使用回溯法进行遍历，势必会出现两个解集[1,7]，一个是[a,b]，另一个是[b,c]，但他们都是解集[1,7]，这是不符合题意的。

关于去重 

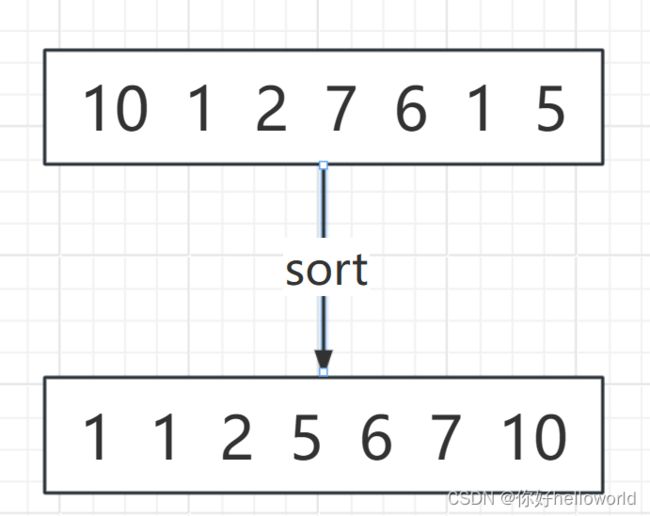
首先我们对candidates 数组进行排序，得到如下序列：

其次，使用回溯法遍历排序后的candidates，如果遇到相邻相同的元素（candidates[i-1]==candidates[i]），跳过即可。

那么接下来的问题就转换成了，如何在回溯法中模拟这个过程？

为方便说明问题，我们假定candidates =[1,1,2],target=3.

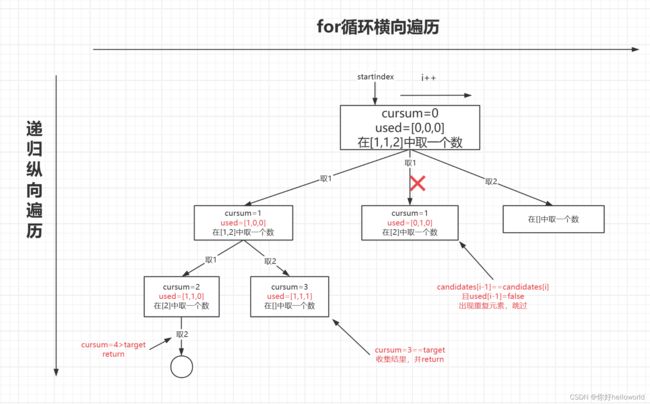
如下图所示，排序后的candidates，如果遇到相邻的相同元素，则必有candidates[i-1]==candidates[i]，但问题在于，这种情况在同一树枝下深度的遍历和同一层的横向遍历都会发生，而我们要的去重是同一树层的去重，也就是在同一层的遍历下，遇到candidates[i-1]==candidates[i]就跳过。

为区别这两种情况，我们使用一个used辅助数组，记录每次取数的过程，也就是说，如果每次取到了一个数，就将used的对应位置置为true。

在下图中可以看出在candidates[i] == candidates[i - 1]相同的情况下：

used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
used[i - 1] == false，说明同一树层candidates[i - 1]使用过

故满足我们要求的去重过程可表示为

如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false，就说明：前一个树枝，使用了candidates[i - 1]，也就是说同一树层使用过candidates[i - 1]。

此时for循环里就应该做continue的操作。

为什么 used[i - 1] == false 就是同一树层呢，因为同一树层，used[i - 1] == false 才能表示，当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的。而 used[i - 1] == true，说明是进入下一层递归，去下一个数，所以是树枝上

详细题解过程参考：40. 组合总和 II - 力扣（LeetCode）https://leetcode.cn/problems/combination-sum-ii/solutions/857552/dai-ma-sui-xiang-lu-dai-ni-xue-tou-hui-s-ig29/

代码

class Solution {
private:
    vector path;
    vector> res;
public:
    void backing(vector& candidates,int target,int startIndex,int curSum,vector& used)
    {
        if(curSum>target) return;
        if(curSum==target)
        {
            res.push_back(path);
            return;
        }

        for(int i=startIndex;i0 && candidates[i-1]==candidates[i] && used[i-1]==false)
            {
                continue;
            }
            else
            {
                curSum+=candidates[i];
                used[i]=true;
                path.push_back(candidates[i]);
                backing(candidates,target,i+1,curSum,used);
                path.pop_back();
                curSum-=candidates[i];
                used[i]=false;
            }
        }
    }
    vector> combinationSum2(vector& candidates, int target) {
        sort(candidates.begin(),candidates.end());
        vector used(candidates.size(),0);
        backing(candidates,target,0,0,used);
        return res;
    }
};