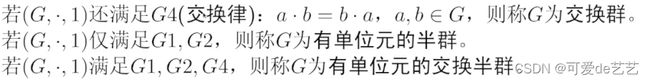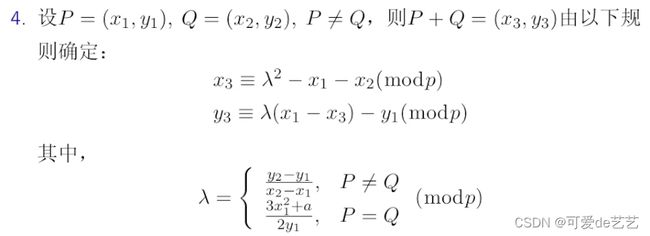信息安全数学基础笔记

三个数学难题:

群的定义:

 满足乘法结合律，有单位元，逆元即为群，如果同时满足交换律则为交换群

满足乘法结合律，有单位元即为半群，如果同时满足交换律则为交换半群 

希尔密码:

 其中加密矩阵为n阶一般线性群，在本例中矩阵元素为0到25的数字

子群：

循环群并定义生成元的概念:

置换的定义:

 也就是一个集合S映射到自己，并且这个映射是双射，则为置换

对称群的概念:

置换密码:对应的是明文中字符位置映射

 第二行是明文的位置，第一行是密文的位置，这里是指把明文第四个位置换到第一个位置，以此类推，解密即为逆映射，把这两行调换即可

代换密码:对应的是字母表上的字母映射

 这里是第一行为明文，第二行为密文，逆映射同样是把两行调换

离散对数问题:

 模n乘:乘完模n，Zn表示0到n-1有n个元素的整数，Zn*表示有素数个元素的集合

  

 如果运算定义成了实数+，那么a^x=a+a+a...共x次，所以是b=xa

环的定义:

交换环的定义:

体和域的概念:

 零因子的概念:

无零因子环及整环的概念:

 这里的Z26表示0到25的数字，乘法表示相乘并mod26，和之前提到的一样

理想的概念:

 直观上理解，一个为加法群的子群，其中任意一个元素与大集合的元素相乘，结果还是这个子群的元素。需要注意，理想是一个群

主理想:

 与理想的区别是I中所有元素都是如上图构成的，且R为交换环

多项式环:

 x前的系数都取自于环R

0多项式的次数的负无穷大，负无穷大和非负整数相加为负无穷大

f(x)的次数为最高项的次数

当最高项的系数为1时，称为首1多项式

定义多项式的乘法和加法:

 

域的定义:

例子:有理数域，实数域，复数域

Galois域:

 其中F中元素的个数称为F的阶

域的性质:

 

 其中要注意   (a*b)^-1=a^-1*b^-1,

                      (-a)^-1=-a^-1

其中上图第一条定理表示域一定为无零因子环、

简单证明：由于域F中每个非零元素a都有逆元素a⁻¹，若a=0或b=0定理成立，若同时不为0，由ab=0，且域中每个非零元素都有逆元，左乘a^-1或右乘b^-1得到a=0或b=0

带余除法:

 这里要求g(x)的次数要大于r(x)的次数

公因式:

 公倍式:

第一个引理的证明:f和g的所有公因式构成一个集合，任取一个m，m能够整除f，而f=pg+r，而m能整除g，则推出m能整除r。所以等式两边集合相等

第二个定理类似于欧几里得算法和扩展的欧几里得算法

例：

既约多项式以及可约多项式:

即除了常数和常数本身之外没有其他因式

既约多项式分解，根:

 

多项式的同余：

 f(x)如果和g(x)关于m(x)同余的话，当且仅当m(x)能整除f(x)-g(x)的差

简单证明一下:

从左到右:f(x)-g(x)=[q1(x)-q2(x)]*m(x)，得到m(x)可以整除二者的差

从右到左:

同余运算的基本性质:

 第一条表明:f和g是同余的，q和r关于m是同余的，则f+q与g+r关于m是同余的，第二三条类似

 第四条表明，若两个式子同余且有相同的因式，则满足什么条件可以在等式两边消去，得到相对简化的同余式

剩余类:

 

 在本例中GF(2)有0，1一共两种元素，n为3，2^3=8

子域，扩域:

数据组与多项式:

多项式可以表示为数字串的形式

有限域上的多项式在高级数据加密标准AES中的应用:(Advanced Encryption Standard)

 

  

 椭圆曲线:

 逐层递进:椭圆曲线，上的点，构成的离散对数问题

 

 Weierstrass方程可以理解为红色的曲面，a1到a6的系数相当于取一个蓝色的平面，曲面和平面相交即为我们看到的曲线

加法原理:

 例子：

 加法原理定理:

有限域上的椭圆曲线:

举例:

 

 在上例，对每个y^2的值，看看是否有整数 mod 23=y^2，此时再找到y值，这样的计算机其实是很困难的

定义Ep(a,b)上的加法

 椭圆曲线密码算法:

数论：研究整数集合

辗转相除法:用来求最大公约数

 

 此时rn即为最大公约数

 

二元一次不定方程:

背包公钥密码算法:

同余式定义:

同余性质:

 第四条表示如果a和b关于mi同余的话，则同时关于他们最小公倍数也是同余的

 第五条表示a是已知的，m是已知的，想要求出x的值

一次同余方程:

 这里的解是指与x0同余的所有x

一次同余方程有解的充要条件:

背包公钥密码:

素数与合数

整数分解定理:

剩余类

 若余数相同则分为一类

完全剩余系:

 是指取出的都比m小

欧拉函数:

欧拉函数计算公式:

 欧拉定理:

费马小定理:

孙子定理:

 这里的Mi为除掉mi的其他m1到mk的乘积,Mi'为同余方程的解

例:

RSA公钥密码算法:

快速幂算法可以算728^675

素数定理:

梅森素数:

 

完全数:

 

整除判别法:

威尔逊判别法:

 

偏序关系:

 自反性:(x,x)成立,哈斯图中表示有自己到自己的一条有向环

反对称性:若x与y不同，如果x<=y,一定没有y>=x

传递性

极小元是指:y，使得不存在x<=y，也是Hasse图的最下层

极大元同理

 最小元是指，必须集合里所有元素都有y<=x，即在Hasse图中是在最下层且与所有元素都有关系的

最大元同理

哈斯图画法:

（1）以“圆圈”表示元素；

（2）若x≤y,则y画在x的上层；

（3）若y覆盖x,则连线；

（4）不可比的元素可画在同一层。

 

在Hassi图中如果上边的元素或者下边的元素不收敛的话，则一定没有上确界或下确界

 全序关系:集合中元素任意两个可以比较

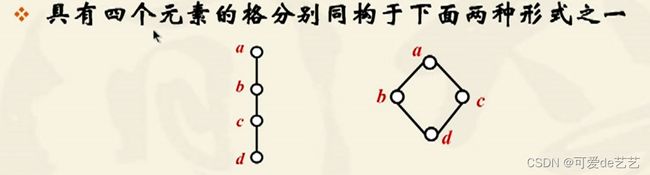
格的对偶:

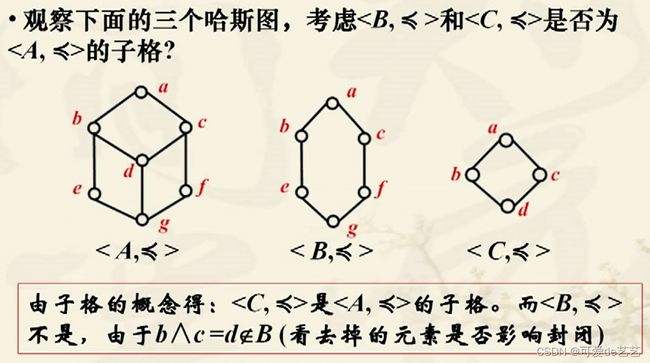
格的同态和同构:

格的性质:

分配不等式:

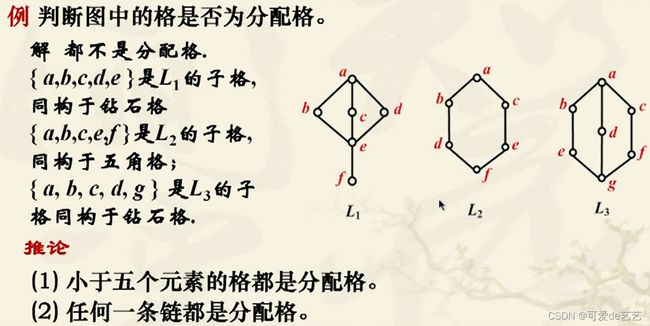
分配格:

 

 

 

 

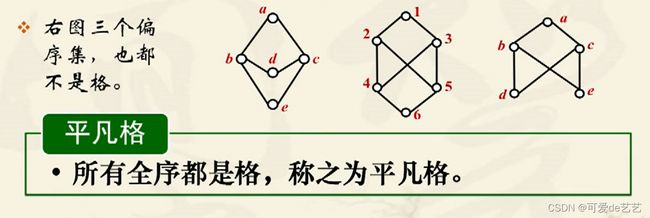
格的全上界与全下界:

有界格:

从Hassi图上来看，格必须有上确界和下确界，要求封闭，所以有限元素的格都是有界格，但无穷元素的格也符合定义但不是有界格

 

有补格:

 

有界分配格:

 

布尔格:

 

布尔代数:

 

 

 

布尔代数的性质:

  

 

 

原子：