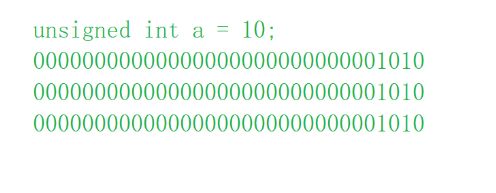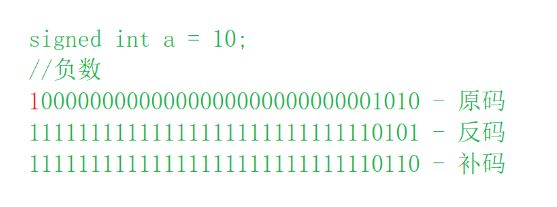你知道C语言的整数和浮点数在内存里是怎么蹦迪的么？？？

• 本篇会加入个人的所谓‘鱼式疯言’
• ❤️❤️❤️鱼式疯言:❤️❤️❤️此疯言非彼疯言,而是理解过并总结出来通俗易懂的大白话,我会尽可能的在每个概念后插入鱼式疯言,帮助大家理解的，可能说的不是那么严谨.但小编初心是能让更多人能接受我们这个概念
  

前言

在本篇文章中，主要讲解的内容有：

1. 整数在内存中的存储
2. ⼤⼩端字节序和字节序判断
3. 浮点数在内存中的存储

一.整数在内存中的存储

1.原码，反码，补码

在讲解操作符的时候，我们就讲过了下⾯的内容：
整数的 2进制 表⽰⽅法有三种，即 原码、反码 和 补码
三种表⽰⽅法均有符号位和数值位两部分，符号位都是⽤0表⽰“正”，⽤1表⽰“负”，⽽数值位最
⾼位的⼀位是被当做符号位，剩余的都是数值位。
对于整型来说：数据存放内存中其实存放的是补码。
为什么呢？
在计算机系统中，数值⼀律⽤补码来表⽰和存储。
原因在于，使⽤补码，可以将符号位和数值域统⼀处理；
同时，加法和减法也可以统⼀处理（CPU只有加法器）
此外，补码与原码相互转换，其运算过程是
相同的，不需要额外的硬件电路。

鱼式疯言

虽然我们整型数值存储的是补码，但当我们用 %d %u 打印时，我们打印的是该数值的原码。

正整数 的原、反、补码都相同。

负整数 的三种表⽰⽅法各不相同。

原码：直接将数值按照正负数的形式翻译成⼆进制得到的就是原码。
反码：将原码的符号位不变，其他位依次按位取反就可以得到反码。
补码：反码+1就得到补码。
这时爱提问的小爱同学就要发问啦？如果我只有这个数字的补码该怎么转化为源码呢？
请欣赏鱼式疯言

当我们的一个补码时
有两种方法可以还原成原码

<1>.减1取反法

<2>.取反加1法

鱼式疯言

这两种方法各特点吧
当我们分不清是哪种方法是我们可以直接记忆第二种方法
当我们需要从补码中得到反码时，我们就可以用第一种方法

2.unsigned与signed

<1>.栗子

#include 
int main()
{
	char a = -1;
	signed char b = -1;
	unsigned char c = -1;
	printf("a=%d,b=%d,c=%d", a, b, c);
	return 0;
}

signed 有符号的
unsigned 无符号的

那么请问？
signed char a；
unsigned char b；

各自的取值范围是多少？

<2>.栗子说明

unsigned char 取值范围 ：0~255
signed char 的取值范围：-128~127

大家知道是什么因素决定了我们signed char 和 unsigned char 的取值范围的不同。

signed char 的取值范围：-128~127


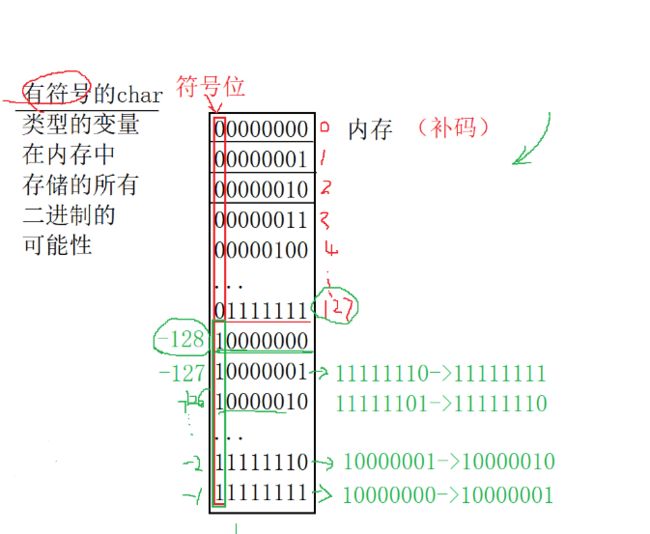
如果超出范围呢 ？
就会循环起来 ！！！

那么无符号的呢？

如果超过最大范围呢？
也会进入循环！！！

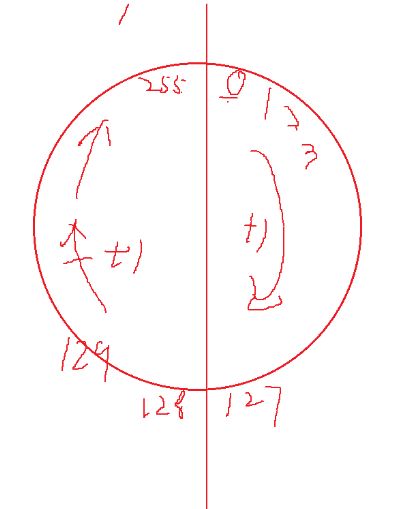
这时爱发问的小爱同学又开始发问啦？
如果我是 signed 要转化为 unsigned 呢？

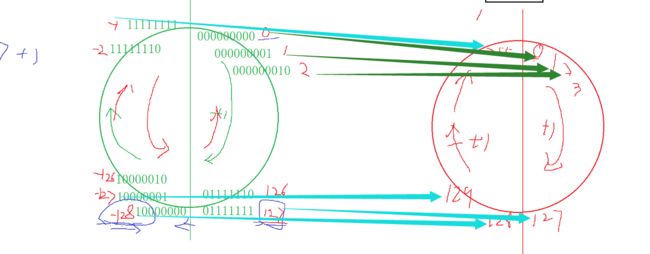
这样就形成了我们的对应关系啦！！！

鱼式疯言

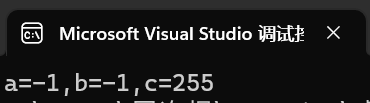
当 signed char -1 转化为 无符号整型 是一个很大的数，
到底这个数是多大呢？ 今天我们就知道答案啦，
他就是unsigned char 类型的 255 。

二.⼤⼩端字节序和字节序判断

1.大小端概念

什么是⼤⼩端？
其实超过⼀个字节的数据在内存中存储的时候，就有存储顺序的问题
按照不同的存储顺序，我们分为⼤端字节序存储和⼩端字节序存储，下⾯是具体的概念：
⼤端（存储）模式：是指数据的低位字节内容保存在内存的⾼地址处
⽽数据的⾼位字节内容，保存在内存的低地址处。
⼩端（存储）模式：是指数据的低位字节内容保存在内存的低地址处，
⽽数据的⾼位字节内容，保存在内存的⾼地址处。
上述概念需要记住，⽅便分辨⼤⼩端。

2.字节序判断

#include
int my_set2(char* x)
{
	return *x;
}
int main()
{
	int a = 1;
	int* p = &a;
	if (my_set2((char*) p))
	{
		printf("小端存储\n");
	}
	else
	{
		printf("大端存储\n");
	}
	return 0;
}

这里用到了强制类型转化，只体现低地址的第一位的字节序

鱼式疯言

小编是这样理解的： 数据编排是从高到低的 就是说 00 00 00 01 依次是
最高，次之，再次之，最低。
所以我们只要判断 低地址
是不是最低位 01，
如果是,证明为最低位存在低地址，为小端存储 反之则为大端存储

三.浮点数在内存中的存储

常⻅的浮点数：3.14159、1E10等，浮点数家族包括： float、double、long double 类型。
那么浮点数的存储是怎么样的呢？
宝子们可以先康康下面的栗子思考下

1.栗子

#include 
int main()
{
	int n = 9;
	float* pFloat = (float*)&n;
	printf("n的值为：%d\n", n);
	printf("*pFloat的值为：%f\n", *pFloat);
	*pFloat = 9.0;
	printf("num的值为：%d\n", n);
	printf("*pFloat的值为：%f\n", *pFloat);
	return 0;
}

相信屏幕前的小朋友
是不是感觉到很匪夷所思呢？
是的，小编第一次看到也感到很奇怪，现在玩算是真正理解了！！！

2.浮点数存储方式

上⾯的代码中， num 和 *pFloat 在内存中明明是同⼀个数，为什么浮点数和整数的解读结果会差别
这么⼤？
要理解这个结果，⼀定要搞懂浮点数在计算机内部的表⽰⽅法。
根据国际标准IEEE（电⽓和电⼦⼯程协会） 754，任意⼀个⼆进制浮点数V可以表⽰成下⾯的形式：
V = (−1) ∗ S M ∗ 2E
• (−1)S 表⽰符号位，当S=0，V为正数；当S=1，V为负数
• M 表⽰有效数字，M是⼤于等于1，⼩于2的
• 2
E 表⽰指数位
举例来说：
⼗进制的5.0，写成⼆进制是 101.0 ，相当于 1.01×2^2 。
那么，按照上⾯V的格式，可以得出S=0，M=1.01，E=2。
⼗进制的-5.0，写成⼆进制是 -101.0 ，相当于 -1.01×2^2 。那么，S=1，M=1.01，E=2。
IEEE 754规定：
对于32位的浮点数，最⾼的1位存储符号位S，接着的8位存储指数E，剩下的23位存储有效数字M
对于64位的浮点数，最⾼的1位存储符号位S，接着的11位存储指数E，剩下的52位存储有效数字M

看到这里是不是眼花缭乱啦，没关系，小编会细细道来！！！

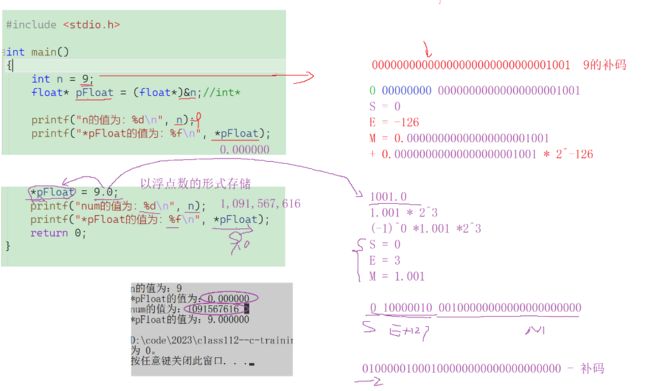
如果是 9.0 的话就转化成二进制

1.先得到(-1)^0

1.0012^3

2.去掉整数部分就得到了我们的上面的
M =1.001

S=0;

E=3;

3.转化成我们字节序第一位符号位为0
4.其次八位为3+127的二进制数：
指数位：10000010
5.数值位：去整数部分后面补充0
00100000000000000000000
6.最终得到
01000001000100000000000000000000

鱼式疯言
注意后面的数值位是和整数相反的，它是后面不0，
如果是单精度float 我们就补充到23位
如果是双进度double 我们就补充到52位


3.E全为 0 或全为 1 的特殊情况

E全为0
这时，浮点数的指数E等于1-127（或者1-1023）即为真实值，有效数字M不再加上第⼀位的1。
⽽是还原为0.xxxxxx的⼩数。这样做是为了表⽰±0，以及接近于0的很⼩的数字。

E全为1
这时，如果有效数字M全为0，表⽰±⽆穷⼤（正负取决于符号位s）。

鱼式疯言

通过以上栗子
我们认识到 浮点数 的存储是比整型数的存储要复杂的多的，而且差别也很大。
宝子们只要掌握基本的转化形式即可

总结

在本篇文章里我们主要讲解了

1. 整数在内存中如何存储的， 无符号 和 有符号 的最大范围和转化
2. ⼤⼩端字节序的概念 和 字节序如何去判断。
3. 浮点数在内存中的存储，我们分为S E M 三个部分的存储方式。

本次博文就到这里了,感觉各位小伙伴的赏脸品读小编写的拙作哦,
如果觉得小编写的还不错的咱可支持三关下,不妥当的咱评论区指正,希望我的文章能给各位家人们带来哪怕一点点的收获就是小编创作的最大动力