【数据结构初阶】链式二叉树的解析及一些基本操作
目录
前置说明
一、 二叉树的遍历（理论）
1. 二叉树的拆解
2. 二叉树的前序（先根）遍历
3. 二叉树的中序（中根）遍历
4. 二叉树的后序（后根）遍历
5. 二叉树的层序遍历
二、 代码实操
1. 前序（先根）遍历代码实现
2. 中序（中根）遍历代码实现
3. 后序（后根）遍历代码实现
4. 求二叉树节点个数
5. 求二叉树叶子节点个数
6. 求二叉树高度
7. 求第k层节点的个数（k>=1）
8. 在二叉树中查找数据为x的节点
9. 层序遍历
10. 判断二叉树是否为完全二叉树
11. 销毁二叉树
三、 测试代码
四、 全部代码
本期博客会详细阐述链式二叉树的一些操作
前置说明
这里由于普通链式二叉树是无规律的，所以对其进行增删查改是无意义的。
在这里并不会对链式二叉树进行增删查改的操作
后面我们还会陆续介绍搜索二叉树、平衡二叉树等等，这些二叉树的增删查改才是有意义的。
一、 二叉树的遍历（理论）
1. 二叉树的拆解
在真正遍历二叉树数之前，我们先要有会拆解二叉树的思想，即把一棵二叉树拆分为多个根和子树。
下面看到这课二叉树：
我们来从上置下从左到右的顺序来拆解这课二叉树
第一次拆解：
先看到总体的二叉树可以被拆分为根为： 
左子树为：
右子树为：
第二次拆解：
我们先拿到第一次拆解的左子树发现其还可以拆解
被拆解后根为：
左子树为：
右子树为：NULL（空树不再进行拆解）
第三次拆解：
我们先拿到第二次拆解的左子树发现其还可以拆解
被拆解后根为：
左子树为：NULL（空树不再进行拆解）
右子树为：NULL（空树不再进行拆解）
第四次拆解：
总体二叉树的左子树已经被全部拆解完毕，接着对第一次拆解的右子树进行拆解
被拆解后根为：
左子树为：
右子树为：
第五次拆解：
接着对第四次拆解的左子树进行拆解
被拆解后根为：
左子树为：NULL（空树不再进行拆解）
右子树为：NULL（空树不再进行拆解）
第六次拆解：
接着对第四次拆解的右子树进行拆解
被拆解后根为：
左子树为：NULL（空树不再进行拆解）
右子树为：NULL（空树不再进行拆解）
经过六次后整个二叉树已经被全部拆解完毕，这样的拆解思想可以称为分治，步步细化层层到位。
2. 二叉树的前序（先根）遍历
二叉树的前序（先根）遍历顺序是先遍历根，再遍历左子树，最后再遍历右子树，以此顺序遍历完整个二叉树。
还是拿这课二叉树来举例：
用前序（先根）遍历的方法遍历的过程为：先遍历整个二叉树的根：A
再遍历A节点的左子树：
该树的根节点为：B
接着遍历B节点的左子树：
该树的根节点为：D
然后再遍历D节点的左子树：NULL（不再向下遍历其根节点）
再遍历D节点的右子树：NULL（不再向下遍历其根节点）
现在B节点的左子树已经遍历完毕再遍历其右子树：NULL（不再向下遍历其根节点）
到这里整个二叉树的左子树已被遍历完毕，再遍历其右子树：
该树的根节点为：C
接着遍历C节点的左子树：
该树的根节点为：E
然后再遍历E节点的左子树：NULL（不再向下遍历其根节点）
再遍历E节点的右子树：NULL（不再向下遍历其根节点）
这里整个C节点的左子树已遍历完毕，再遍历其右子树：
该树的根节点为：F
然后再遍历F节点的左子树：NULL（不再向下遍历其根节点）
再遍历F节点的右子树：NULL（不再向下遍历其根节点）
最终整个二叉树的右子树也被遍历完成，前序（先根）遍历完成。
总顺序为：A->B->D->NULL->NULL->NULL->C->E->NULL->NULL->F->NULL->NULL
3. 二叉树的中序（中根）遍历
二叉树的中序（中根）遍历顺序是先遍左子树，再遍历根，最后再遍历右子树，以此顺序遍历完整个二叉树。
再是拿这课二叉树来举例：
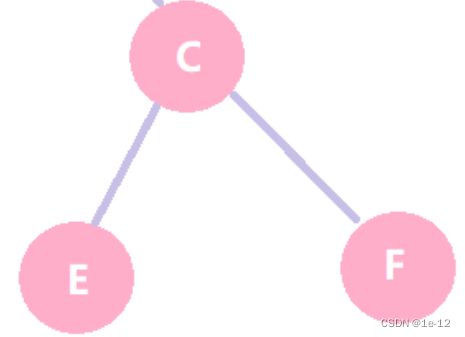
用中序（中根）遍历的方法遍历的过程为：先遍历整个二叉树的左子树：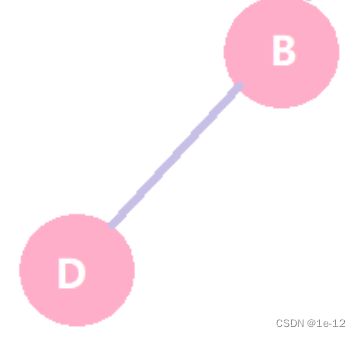
再遍历以B为根节点的左子树：
接着遍历以D为根节点的左子树：NULL（不再向下遍历其左子树）
以D为根节点的左子树遍历完了，接着遍历其根：D
以D为根节点的树的根遍历完了，接着遍历其右子树：NULL（不再向下遍历其左子树）
以B为根节点的左子树遍历完了，接着遍历其根：B
以B为根节点的树的根遍历完了，接着遍历其右子树：NULL（不再向下遍历其左子树）
整个二叉树的左子树遍历完了，接着遍历其根：A
整个二叉树的根遍历完了，接着遍历其右子树：
再遍历以C为根节点的左子树：
接着遍历以E为根节点的左子树：NULL（不再向下遍历其左子树）
以E为根节点的左子树遍历完了，接着遍历其根：E
以E为根节点的树的根遍历完了，接着遍历其右子树：NULL（不再向下遍历其左子树）
以C为根节点的左子树遍历完了，接着遍历其根：C
以C为根节点的树的根遍历完了，接着遍历其右子树：
接着遍历以F为根节点的左子树：NULL（不再向下遍历其左子树）
以F为根节点的左子树遍历完了，接着遍历其根：F
以F为根节点的树的根遍历完了，接着遍历其右子树：NULL（不再向下遍历其左子树）
最终随着以C为根节点的右子树遍历完了，整个二叉树的右子树也被遍历完成，中序（中根）遍历完成。
总顺序为：NULL->D->NULL->B->NULL->A->NULL->E->NULL->C->NULL->F->NULL
4. 二叉树的后序（后根）遍历
二叉树的后序（后根）遍历顺序是先遍左子树，再遍历右子树，最后再遍历根，以此顺序遍历完整个二叉树。
还是拿这课二叉树来举例：
用后序（后根）遍历的方法遍历的过程为：先遍历整个二叉树的左子树：
再遍历以B为根节点的左子树：
接着遍历以D为根节点的左子树：NULL（不再向下遍历其左子树）
以D为根节点的左子树遍历完了，接着遍历其右子树：NULL（不再向下遍历其左子树）
以D为根节点的右子树遍历完了，接着遍其根：D
以B为根节点的左子树遍历完了，接着遍历其右子树：NULL（不再向下遍历其左子树）
以B为根节点的右子树遍历完了，接着遍其根：B
整个二叉树的左子树遍历完了，接着遍历其右子树：
再遍历以C为根节点的左子树：
接着遍历以E为根节点的左子树：NULL（不再向下遍历其左子树）
以E为根节点的左子树遍历完了，接着遍历其右子树：NULL（不再向下遍历其左子树）
以E为根节点的右子树遍历完了，接着遍其根：E
以C为根节点的左子树遍历完了，接着遍历其右子树：
接着遍历以F为根节点的左子树：NULL（不再向下遍历其左子树）
以F为根节点的左子树遍历完了，接着遍历其右子树：NULL（不再向下遍历其左子树）
以F为根节点的右子树遍历完了，接着遍历其根：F
以C为根节点的右子树遍历完了，接着遍其根：C
整个二叉树的右子树也被遍历完成，接着遍其根：A
后序（后根）遍历完成。
总顺序为：NULL->NULL->D->NULL->B->NULL->NULL->E->NULL->NULL->F->C->A
5. 二叉树的层序遍历
二叉树的层序遍历顺序是先左后右从上到下，一层一层遍历，以此顺序遍历完整个二叉树。
这个二叉树用层序遍历就是：A->B->C->D->E->F
二、 代码实操
下面我们来用代码来对二叉树进行一些基本操作
下面是对链式二叉树节点的代码结构：
typedef char DataType;
typedef struct BinaryTreeNode
{
//数据
DataType data;
struct BinaryTreeNode* Left;//指向左孩子
struct BinaryTreeNode* Right;//指向右孩子
}BTNode;1. 前序（先根）遍历代码实现
void PrevOrder(BTNode* root)//传入二叉树根节点
{
if (root == NULL)//如果是空树就直接结束
{
printf("NULL ");
return;
}
printf("%c ", root->data);//先遍历其根节点
PrevOrder(root->Left);//递归遍历其左子树
PrevOrder(root->Right);//递归遍历其右子树
}2. 中序（中根）遍历代码实现
void InOrder(BTNode* root)
{
if (root == NULL)//如果是空树就直接结束
{
printf("NULL ");
return;
}
InOrder(root->Left);//先递归遍历其左子树
printf("%c ", root->data);//再遍历其根节点
InOrder(root->Right);//最后递归遍历其右子树
}3. 后序（后根）遍历代码实现
void PostOrder(BTNode* root)
{
if (root == NULL)//如果是空树就直接结束
{
printf("NULL ");
return;
}
PostOrder(root->Left);//先递归遍历其左子树
PostOrder(root->Right);//再递归遍历其右子树
printf("%c ", root->data);//最后遍历其根节点
}4. 求二叉树节点个数
在求二叉树节点个数时，我们不能单一定义一个局部变量来实现，也不能定义一个静态变量来统计节点个数（静态变量除第一次再被函数调用时初始值是不一样的），在这里我们使用全局变量来实现：
int size = 0;
void CountTreeSize(BTNode* root)
{
if (root == NULL)
{
return;
}
size++;
CountTreeSize(root->Left);
CountTreeSize(root->Right);
}
void TreeSize(BTNode* root)
{
size = 0;//防止多次调用时初始值发生改变
CountTreeSize(root);
}
但是还有一个更好的方法：
int TreeSize2(BTNode* root)
{
return root == NULL ? 0 : TreeSize2(root->Left) + TreeSize2(root->Right) + 1;
}这里我们层层递归统计最后将值合计返回（妙）！
5. 求二叉树叶子节点个数
int TreeLeafSize(BTNode* root)
{
if (root == NULL)//防止指针越界
return 0;
if (root->Left == NULL && root->Right == NULL)//是叶子节点就返回1
return 1;
return TreeLeafSize(root->Left) + TreeLeafSize(root->Right);//累加所有的返回值
}6. 求二叉树高度
int TreeHeight(BTNode* root)
{
if (root == NULL)
return 0;
int LeftHeight = TreeHeight(root->Left);//记录左子树深度
int RightHeight = TreeHeight(root->Right);//记录右子树深度
return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;//返回较大子树的深度
}7. 求第k层节点的个数（k>=1）
int TreeKLevelSize(int k, BTNode* root)
{
if (root == NULL)
return 0;
if (k == 1)//k=1是即是节点处于原本k层
return 1;
return TreeKLevelSize(k - 1, root->Left) + TreeKLevelSize(k - 1, root->Right);//每次递归到下一层k值减1
}8. 在二叉树中查找数据为x的节点
BTNode* TreeFind(BTNode* root,DataType x)
{
if (root == NULL)
return NULL;
if (root->data == x)//找到返回其地址
return root;
BTNode* ret1 = TreeFind(root->Left, x);//在左子树中递归寻找
if (ret1)//找到了返回其地址
return ret1;
BTNode* ret2 = TreeFind(root->Right, x);//在右子树中递归寻找
if (ret2)//找到了返回其地址
return ret2;
return NULL;
}9. 层序遍历
在我们层序遍历二叉树时可以使用队列来保存二叉树的节点：即在遍历一个二叉树节点后将其左右孩子入队列，在遍历节点时队头出一个节点数据（直到队列为空结束遍历）。于是我们在这里需要用到一些队列的基本操作：
//数据
typedef BTNode* QDataType;
//链表节点
typedef struct QListNode
{
struct QListNode* _next;
QDataType _data;
}QNode;
// 队列的结构
typedef struct Queue
{
QNode* _front;//队头
QNode* _rear;//队尾
int size;//记录节点总数
}Queue;
// 初始化队列
void QueueInit(Queue* q)
{
assert(q);//传入的指针不能为空
//将队头和队尾指针都初始化为空
q->_front = NULL;
q->_rear = NULL;
q->size = 0;//置0
}
// 检测队列是否为空
bool QueueEmpty(Queue* q)
{
assert(q);//传入的指针不能为空
return q->_front == NULL && q->_rear == NULL;//如果队头队尾指针都为空返回的就是真值
}
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
assert(q);//传入的指针不能为空
QNode* newnode = (QNode*)malloc(sizeof(QNode));//为新元素开辟空间
if (newnode == NULL)//判断是否开辟成功
{
perror("malloc");
exit(-1);
}
newnode->_data = data;
newnode->_next = NULL;
//注意这里尾插时要判断队中是否为空，是空的话需要改变队头和队尾指针的指向
if (QueueEmpty(q))
{
q->_front = q->_rear = newnode;
}
else
{
q->_rear->_next = newnode;
q->_rear = q->_rear->_next;
}
q->size++;//加1
}
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);//传入的指针不能为空
assert(!QueueEmpty(q));//队列不能为空
QNode* del = q->_front;
//注意这里尾插时要判断队中是否为空，如果是的话需要将队头队尾指针置为空
if (q->_front == q->_rear)
{
q->_front = q->_rear = NULL;
}
else
{
q->_front = q->_front->_next;
}
free(del);//释放节点空间
q->size--;//减1
}
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{
assert(q);//传入的指针不能为空
assert(!QueueEmpty(q));//队列不能为空
return q->_front->_data;//返回队列头部元素
}
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);//传入的指针不能为空
QNode* cur = q->_front;
//释放链表空间
while (cur)
{
QNode* del = cur;
cur = cur->_next;
free(del);
}
//将队头和队尾指针置空(防止野指针的产生)
q->_front = q->_rear = NULL;
q->size = 0;//置0
}
void LevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root != NULL)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%c ", front->data);
if (front->Left != NULL)
QueuePush(&q, front->Left);
if (front->Right != NULL)
QueuePush(&q, front->Right);
}
printf("\n");
QueueDestroy(&q);
}10. 判断二叉树是否为完全二叉树
判断二叉树是否为完全二叉树我们可以先对二叉树进行层序遍历，遍历到空节点时跳出遍历，然后检查队列中节点指针是否全为空（完全二叉树在最后一个叶子节点之后的节点应当全为空）。
bool BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root != NULL)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
break;
else
{
QueuePush(&q, front->Left);
QueuePush(&q, front->Right);
}
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front != NULL)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}11. 销毁二叉树
销毁二叉树时，我们可以遍历一个节点释放一个节点
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL)
return;
BinaryTreeDestory(root->Left);
BinaryTreeDestory(root->Right);
free(root);
}三、 测试代码
BTNode* BuyBTNode(DataType x)//为二叉树节点申请空间
{
BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
if (newNode == NULL)
{
perror("malloc");
exit(-1);
}
newNode->data = x;
newNode->Left = NULL;
newNode->Right = NULL;
return newNode;
}
void Test()
{
BTNode* n1 = BuyBTNode('A');
BTNode* n2 = BuyBTNode('B');
BTNode* n3 = BuyBTNode('C');
BTNode* n4 = BuyBTNode('D');
BTNode* n5 = BuyBTNode('E');
BTNode* n6 = BuyBTNode('F');
BTNode* n7 = BuyBTNode('G');
n1->Left = n2;
n1->Right = n3;
n2->Left = n4;
n3->Left = n5;
n3->Right = n6;
n6->Left = n7;
//上面都是手动构建二叉树
PrevOrder(n1);
printf("\n");
InOrder(n1);
printf("\n");
PostOrder(n1);
printf("\n");
TreeSize(n1);
printf("Tree Size:%d\n", size);
TreeSize(n1);
printf("Tree Size:%d\n", size);
TreeSize(n1);
printf("Tree Size:%d\n", TreeSize2(n1));
printf("Tree Leaf Size:%d\n", TreeLeafSize(n1));
printf("Tree Height:%d\n", TreeHeight(n1));
printf("Tree 3 level Size:%d\n", TreeKLevelSize(3, n1));
printf("The address of E is : %p\n", TreeFind(n1, 'E'));
LevelOrder(n1);
printf("BinaryTreeComplete:%d\n", BinaryTreeComplete(n1));
BinaryTreeDestory(n1);
}下面是测试结果：
四、 全部代码
#include
#include
#include
#include
typedef char DataType;
typedef struct BinaryTreeNode
{
//数据
DataType data;
struct BinaryTreeNode* Left;//指向左孩子
struct BinaryTreeNode* Right;//指向右孩子
}BTNode;
void PrevOrder(BTNode* root)//传入二叉树根节点
{
if (root == NULL)//如果是空树就直接结束
{
printf("NULL ");
return;
}
printf("%c ", root->data);//先遍历其根节点
PrevOrder(root->Left);//递归遍历其左子树
PrevOrder(root->Right);//递归遍历其右子树
}
void InOrder(BTNode* root)
{
if (root == NULL)//如果是空树就直接结束
{
printf("NULL ");
return;
}
InOrder(root->Left);//先递归遍历其左子树
printf("%c ", root->data);//再遍历其根节点
InOrder(root->Right);//最后递归遍历其右子树
}
void PostOrder(BTNode* root)
{
if (root == NULL)//如果是空树就直接结束
{
printf("NULL ");
return;
}
PostOrder(root->Left);//先递归遍历其左子树
PostOrder(root->Right);//再递归遍历其右子树
printf("%c ", root->data);//最后遍历其根节点
}
int size = 0;
void CountTreeSize(BTNode* root)
{
if (root == NULL)
{
return;
}
size++;
CountTreeSize(root->Left);
CountTreeSize(root->Right);
}
void TreeSize(BTNode* root)
{
size = 0;//防止多次调用时初始值发生改变
CountTreeSize(root);
}
int TreeSize2(BTNode* root)
{
return root == NULL ? 0 : TreeSize2(root->Left) + TreeSize2(root->Right) + 1;
}
int TreeLeafSize(BTNode* root)
{
if (root == NULL)//防止指针越界
return 0;
if (root->Left == NULL && root->Right == NULL)//是叶子节点就返回1
return 1;
return TreeLeafSize(root->Left) + TreeLeafSize(root->Right);//累加所有的返回值
}
int TreeHeight(BTNode* root)
{
if (root == NULL)
return 0;
int LeftHeight = TreeHeight(root->Left);//记录左子树深度
int RightHeight = TreeHeight(root->Right);//记录右子树深度
return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;//返回较大子树的深度
}
int TreeKLevelSize(int k, BTNode* root)
{
if (root == NULL)
return 0;
if (k == 1)//k=1是即是节点处于原本k层
return 1;
return TreeKLevelSize(k - 1, root->Left) + TreeKLevelSize(k - 1, root->Right);//每次递归到下一层k值减1
}
BTNode* TreeFind(BTNode* root,DataType x)
{
if (root == NULL)
return NULL;
if (root->data == x)//找到返回其地址
return root;
BTNode* ret1 = TreeFind(root->Left, x);//在左子树中递归寻找
if (ret1)//找到了返回其地址
return ret1;
BTNode* ret2 = TreeFind(root->Right, x);//在右子树中递归寻找
if (ret2)//找到了返回其地址
return ret2;
return NULL;
}
//数据
typedef BTNode* QDataType;
//链表节点
typedef struct QListNode
{
struct QListNode* _next;
QDataType _data;
}QNode;
// 队列的结构
typedef struct Queue
{
QNode* _front;//队头
QNode* _rear;//队尾
int size;//记录节点总数
}Queue;
// 初始化队列
void QueueInit(Queue* q)
{
assert(q);//传入的指针不能为空
//将队头和队尾指针都初始化为空
q->_front = NULL;
q->_rear = NULL;
q->size = 0;//置0
}
// 检测队列是否为空
bool QueueEmpty(Queue* q)
{
assert(q);//传入的指针不能为空
return q->_front == NULL && q->_rear == NULL;//如果队头队尾指针都为空返回的就是真值
}
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
assert(q);//传入的指针不能为空
QNode* newnode = (QNode*)malloc(sizeof(QNode));//为新元素开辟空间
if (newnode == NULL)//判断是否开辟成功
{
perror("malloc");
exit(-1);
}
newnode->_data = data;
newnode->_next = NULL;
//注意这里尾插时要判断队中是否为空，是空的话需要改变队头和队尾指针的指向
if (QueueEmpty(q))
{
q->_front = q->_rear = newnode;
}
else
{
q->_rear->_next = newnode;
q->_rear = q->_rear->_next;
}
q->size++;//加1
}
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);//传入的指针不能为空
assert(!QueueEmpty(q));//队列不能为空
QNode* del = q->_front;
//注意这里尾插时要判断队中是否为空，如果是的话需要将队头队尾指针置为空
if (q->_front == q->_rear)
{
q->_front = q->_rear = NULL;
}
else
{
q->_front = q->_front->_next;
}
free(del);//释放节点空间
q->size--;//减1
}
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{
assert(q);//传入的指针不能为空
assert(!QueueEmpty(q));//队列不能为空
return q->_front->_data;//返回队列头部元素
}
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);//传入的指针不能为空
QNode* cur = q->_front;
//释放链表空间
while (cur)
{
QNode* del = cur;
cur = cur->_next;
free(del);
}
//将队头和队尾指针置空(防止野指针的产生)
q->_front = q->_rear = NULL;
q->size = 0;//置0
}
void LevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root != NULL)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%c ", front->data);
if (front->Left != NULL)
QueuePush(&q, front->Left);
if (front->Right != NULL)
QueuePush(&q, front->Right);
}
printf("\n");
QueueDestroy(&q);
}
bool BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root != NULL)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
break;
else
{
QueuePush(&q, front->Left);
QueuePush(&q, front->Right);
}
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front != NULL)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL)
return;
BinaryTreeDestory(root->Left);
BinaryTreeDestory(root->Right);
free(root);
}
BTNode* BuyBTNode(DataType x)//为二叉树节点申请空间
{
BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
if (newNode == NULL)
{
perror("malloc");
exit(-1);
}
newNode->data = x;
newNode->Left = NULL;
newNode->Right = NULL;
return newNode;
}
本期博客到这里又要和大家说再见了，后面还会为各位看客带来二叉树更深入的讲解，请不要走开~
本期含递归代码较多，有较难理解的地方需要多画图慢慢消化，如有纰漏还请各位大佬不吝赐教呀
我们下期见！