常微分方程组的数值解法(C++)
常微分方程组的数值解法是一种数学方法, 用于求解一组多元的常微分方程(Ordinary Differential Equations, ODEs). 常微分方程组通常描述了多个变量随时间或其他独立变量的演化方式, 这些方程是自然界和工程问题中的常见数学建模工具. 解这些方程组的确切解通常难以找到, 因此需要数值方法来近似解. 与常微分方程数值解法类似, 常微分方程组的数值解法也有相应的Euler法和Runge-Kutta法.
Euler法
考虑一阶常微分方程初值问题
{ d y i d x = f i ( x , y 1 , ⋯ , y N ) y i ( x 0 ) = y i 0 \begin{cases} \dfrac{{\rm d}y_i}{{\rm d}x}=f_i(x,y_1,\cdots,y_N)\\ y_i(x_0)=y_{i0} \end{cases} ⎩⎨⎧dxdyi=fi(x,y1,⋯,yN)yi(x0)=yi0
若令
y = ( y 1 , ⋯ , y N ) T \bm y=(y_1,\cdots,y_N)^T y=(y1,⋯,yN)T
f = ( f 1 , ⋯ , f N ) T \bm f=(f_1,\cdots,f_N)^T f=(f1,⋯,fN)T
则上式可以表示为
{ d y d x = f ( x , y ) y ( x 0 ) = y 0 \begin{cases} \dfrac{{\rm d}\bm y}{{\rm d}x}=\bm f(x,\bm y)\\ \bm y(x_0)=\bm y_0 \end{cases} ⎩⎨⎧dxdy=f(x,y)y(x0)=y0
类似于一个方程时的情形, 我们可以推出多元的显式Euler法如下:
y k + 1 = y k + h f ( x k , y k ) \bm y_{k+1}=\bm y_k+h\bm f(x_k,\bm y_k) yk+1=yk+hf(xk,yk)
Runge-Kutta法
Runge-Kutta法也是类似的, 只需将相应的标量函数替换为向量函数. 这里仅给出经典4阶Runge-Kutta法:
{ K 1 = f ( x k , y k ) K 2 = f ( x k + h 2 , y k + h 2 K 1 ) K 3 = f ( x k + h 2 , y k + h 2 K 2 ) K 4 = f ( x k + h , y k + h K 3 ) y k + 1 = y k + h 6 ( K 1 + 2 K 2 + 2 K 3 + K 4 ) \begin{cases} \bm K_1=\bm f(x_k,\bm y_k)\\ \bm K_2=\bm f\left(x_k+\dfrac h2,\bm y_k+\dfrac h2\bm K_1\right)\\ \bm K_3=\bm f\left(x_k+\dfrac h2,\bm y_k+\dfrac h2\bm K_2\right)\\ \bm K_4=\bm f(x_k+h,\bm y_k+h\bm K_3)\\ \bm y_{k+1}=\bm y_k+\dfrac h6(\bm K_1+2\bm K_2+2\bm K_3+\bm K_4) \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧K1=f(xk,yk)K2=f(xk+2h,yk+2hK1)K3=f(xk+2h,yk+2hK2)K4=f(xk+h,yk+hK3)yk+1=yk+6h(K1+2K2+2K3+K4)
算法实现
首先进行预处理如下:
#include 接着实现一个输出迭代过程到文件的函数:
namespace _MYFUNCTION
{
static void print_vec()
{
double *p(vec_begin);
fprintf(file, "%.14f", *p);
unsigned m(n);
while (--m)
fprintf(file, ",%.14f", *++p);
}
}
判断向量是否为有效值:
bool isnan(const vec &x)
{
for (const auto &i : x)
if (isnan(i))
return true;
return false;
}
显式Euler法的实现:
/*
* 显式欧拉法
* P:文件保存路径
* f:显式微分方程的右端函数
* a:区间左端点
* b:区间右端点
* y0:解在x0处的初值
* h:步长
* x0:初值点
*
* 不检查函数f的维数问题
*/
void Euler(const char *P, const func &f, const double &a, const double &b, const vec &y0, const double &h, double x0)
{
if (a >= b)
throw "区间左端点小于区间右端点!";
if (x0 < a || x0 > b)
throw "初值点不在区间内!";
if (!h)
throw "步长为零!";
vec y(y0);
n = y0.n_elem;
vec_begin = &y.at(0);
if (fopen_s(&file, P, "w"))
throw "文件保存失败!";
fprintf(file, "%.14f,", x0);
_MYFUNCTION::print_vec();
double x(x0);
if (h > 0)
while ((x0 += h) <= b)
{
EX6T2_JUDGE_NAN(y += h * f(x, y))
fprintf(file, "\n%.14f,", x = x0);
_MYFUNCTION::print_vec();
}
else
while ((x0 += h) >= a)
{
EX6T2_JUDGE_NAN(y += h * f(x, y))
fprintf(file, "\n%.14f,", x = x0);
_MYFUNCTION::print_vec();
}
fclose(file);
}
/*
* 显式欧拉法
* P:文件保存路径
* f:显式微分方程的右端函数
* a:区间左端点
* b:区间右端点
* y0:解在x0处的初值
* h:步长
*
* 不检查函数f的维数问题
*/
inline void Euler(const char *P, const func &f, const double &a, const double &b, const vec &y0, const double &h = 0.0078125)
{
return Euler(P, f, a, b, y0, h, a);
}
经典4阶Runge-Kutta法的实现:
/*
* 4阶Runge-Kutta法
* P:文件保存路径
* f:显式微分方程的右端函数
* a:区间左端点
* b:区间右端点
* y0:解在x0处的初值
* h:步长
* x0:初值点
*
* 不检查函数f的维数问题
*/
void Runge_Kutta4(const char *P, const func &f, const double &a, const double &b, const vec &y0, const double &h, double x0)
{
if (a >= b)
throw "区间左端点小于区间右端点!";
if (x0 < a || x0 > b)
throw "初值点不在区间内!";
if (!h)
throw "步长为零!";
vec y(y0);
n = y0.n_elem;
vec_begin = &y.at(0);
if (fopen_s(&file, P, "w"))
throw "文件保存失败!";
fprintf(file, "%.14f,", x0);
_MYFUNCTION::print_vec();
double x(x0), h2(h / 2), h6(h2 / 3);
if (h > 0)
while ((x0 += h) <= b)
{
vec k1(f(x, y));
EX6T2_JUDGE_NAN(k1)
vec k2(f(x += h2, y + h2 * k1));
EX6T2_JUDGE_NAN(k2)
vec k3(f(x, y + h2 * k2));
EX6T2_JUDGE_NAN(k3)
vec k4(f(x0, y + h * k3));
EX6T2_JUDGE_NAN(k4)
y += h6 * (k1 + k4 + 2 * (k2 + k3));
fprintf(file, "\n%.14f,", x = x0);
_MYFUNCTION::print_vec();
}
else
while ((x0 += h) >= a)
{
vec k1(f(x, y));
EX6T2_JUDGE_NAN(k1)
vec k2(f(x += h2, y + h2 * k1));
EX6T2_JUDGE_NAN(k2)
vec k3(f(x, y + h2 * k2));
EX6T2_JUDGE_NAN(k3)
vec k4(f(x0, y + h * k3));
EX6T2_JUDGE_NAN(k4)
y += h6 * (k1 + k4 + 2 * (k2 + k3));
fprintf(file, "\n%.14f,", x = x0);
_MYFUNCTION::print_vec();
}
fclose(file);
}
/*
* 4阶Runge-Kutta法
* P:文件保存路径
* f:显式微分方程的右端函数
* a:区间左端点
* b:区间右端点
* y0:解在x0处的初值
* h:步长
*
* 不检查函数f的维数问题
*/
inline void Runge_Kutta4(const char *P, const func &f, const double &a, const double &b, const vec &y0, const double &h = 0.0078125)
{
return Runge_Kutta4(P, f, a, b, y0, h, a);
}
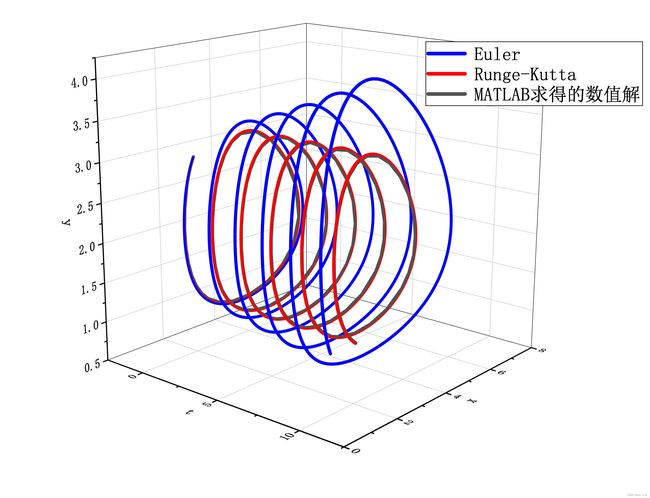
实例分析
求解如下微分方程组:
{ d x d t = 4 x − 2 x y d y d t = x y − 3 y x ( 0 ) = 2 , y ( 0 ) = 3 \begin{cases} \dfrac{{\rm d}x}{{\rm d}t}=4x-2xy\\ \dfrac{{\rm d}y}{{\rm d}t}=xy-3y\\ x(0)=2,y(0)=3 \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧dtdx=4x−2xydtdy=xy−3yx(0)=2,y(0)=3