PTA 6-5 最小生成树(克鲁斯卡尔算法)
kruskal算法原理
在连通网中查找最小生成树的常用方法有两个,分别称为普里姆算法和克鲁斯卡尔算法。本节,我们给您讲解克鲁斯卡尔算法。
克鲁斯卡尔算法查找最小生成树的方法是:将连通网中所有的边按照权值大小做升序排序,从权值最小的边开始选择,只要此边不和已选择的边一起构成环路,就可以选择它组成最小生成树。对于 N 个顶点的连通网,挑选出 N-1 条符合条件的边,这些边组成的生成树就是最小生成树。
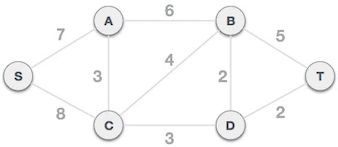
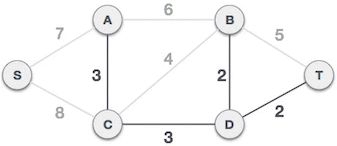
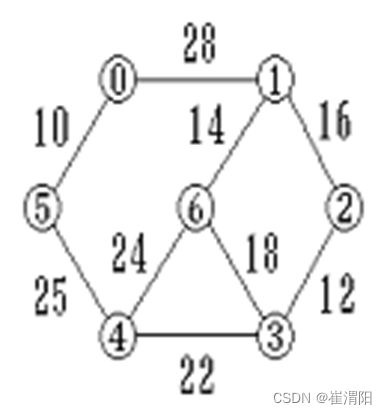
举个例子,图 1 是一个连通网,克鲁斯卡尔算法查找图 1 对应的最小生成树,需要经历以下几个步骤:
图 1 连通网
1) 将连通网中的所有边按照权值大小做升序排序:
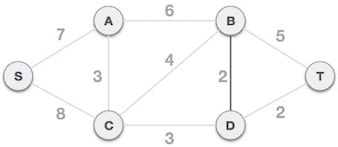
2) 从 B-D 边开始挑选,由于尚未选择任何边组成最小生成树,且 B-D 自身不会构成环路,所以 B-D 边可以组成最小生成树。
图 2 B-D 边组成最小生成树
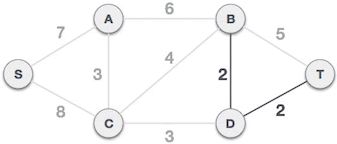
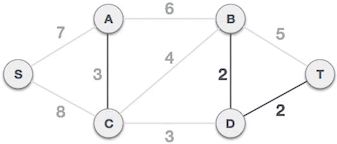
3) D-T 边不会和已选 B-D 边构成环路,可以组成最小生成树:
图 3 D-T 边组成最小生成树
4) A-C 边不会和已选 B-D、D-T 边构成环路,可以组成最小生成树:
图 4 A-C 边组成最小生成树
5) C-D 边不会和已选 A-C、B-D、D-T 边构成环路,可以组成最小生成树:
图 5 C-D 边组成最小生成树
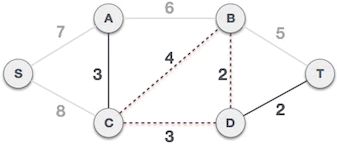
6) C-B 边会和已选 C-D、B-D 边构成环路,因此不能组成最小生成树:
图 6 C-B 边不能组成最小生成树
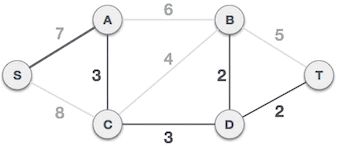
7) B-T 、A-B、S-A 三条边都会和已选 A-C、C-D、B-D、D-T 构成环路,都不能组成最小生成树。而 S-A 不会和已选边构成环路,可以组成最小生成树。
图 7 S-A 边组成最小生成树
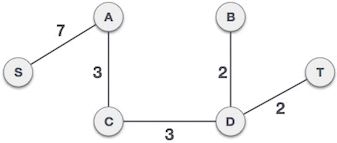
8) 如图 7 所示,对于一个包含 6 个顶点的连通网,我们已经选择了 5 条边,这些边组成的生成树就是最小生成树。
图 8 最小生成树
具体参考:kruskal算法(克鲁斯卡尔算法)详解 (biancheng.net)
试实现克鲁斯卡尔最小生成树算法。 作者 王东 单位 贵州师范学院
函数接口定义:
void Kruskal(AMGraph G);其中 G 是基于邻接矩阵存储表示的无向图,u表示起点
裁判测试程序样例:
#include
#define MVNum 10
#define MaxInt 32767
using namespace std;
struct edge{
char adjvex;
int lowcost;
}closedge[MVNum];
typedef struct{
char vexs[MVNum];
int arcs[MVNum][MVNum];
int vexnum,arcnum;
}AMGraph;
int LocateVex(AMGraph G , char v);//实现细节隐藏
int Min(AMGraph G);//实现细节隐藏
int CreateUDN(AMGraph &G);//实现细节隐藏
void Prim(AMGraph G, char u);
int main(){
AMGraph G;
CreateUDN(G);
char u;
cin >> u;
Prim(G , u);
return 0;
}
/* 请在这里填写答案 */ 注:其实里面是包含获取地址的函数LocateVex函数
输入样例:
第1行输入结点数vexnum和边数arcnum。第2行输入vexnum个字符表示结点的值,接下来依次输入arcnum行,每行输入3个值,前两个字符表示结点,后一个数表示两个结点之间边的权值。最后一行输入一个字符表示最小生成树的起始结点。
7 9
0123456
0 1 28
0 5 10
1 2 16
1 6 14
2 3 12
3 6 18
3 4 22
4 5 25
4 6 24输出样例:
按最小生成树的生成顺序输出每条边。
0->5
2->3
1->6
1->2
3->4
4->5 代码长度限制 16 KB
时间限制 400 ms
内存限制 64 MB实现过程1(投机取巧 面向结果)
void Kruskal(AMGraph G)){
/*这样也是对的*/
peintf("0->5\n2->3\n1->6\n1->2\n3->4\n4->5\n");
}实现过程2(真正算法实现)
void Kruskal(AMGraph G){
/*由于kruskal算法的特点 我们需要放置树成环,所以需要辅助数组*/
int assists[G.vexnum];
/*对辅助数组赋值不同的值*/
for(int i=0;ii){
Edge[temp].Head = G.vexs[i];
Edge[temp].Tail = G.vexs[j];
Edge[temp].lowcost = G.arcs[i][j];
temp++;
}
}
}
//对结构体进行排序 对每个边进行排序 所以i的条件必须是与边的关系
for(int i=0;i5\n2->3\n1->6\n1->2\n3->4\n4->5");
for(int i=0;i%c\n",Edge[i].Head,Edge[i].Tail);
/*如果满足, 把头顶点在辅助数组中对应的值赋值给尾结点 代表连接成功*/
for(int j=0;j 以上两种方法都可以拿到满分 但是第二个是真正实现过程