【二叉树专题】—— 遍历二叉树

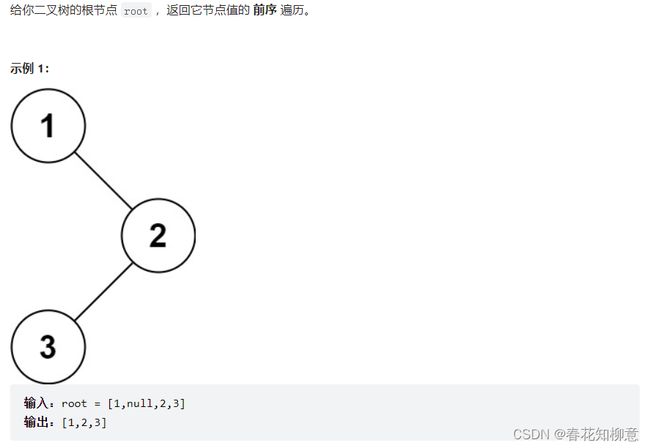
LeetCode 144： 二叉树的前序遍历

解题思路：

（1）二叉树的前序遍历：

重复子问题： 根结点 左子树 右子树
递归结束条件： 当前结点为空

（2）此题需要一个List集合来维护遍历过的结点的值

• ArrayList 与 LinkedList 的区别：

两者都实现了List的接口，前者的底层是数组，后者的底层是链表
前者便于查找，时间复杂度为O(1);后者便于添加和删除，但后者需要更多的存储空间

Java递归版本:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    //设计一个方法，来完成前序遍历与结点值的记录
    public  void preorder(TreeNode root, ArrayList res){
        //如果当前结果为空，那么直接返回空
        if(root == null){
            return;
        }

        res.add(root.val);

        //递归左子树
        preorder(root.left, res);
        //递归右子树
        preorder(root.right, res);

    }

    public List<Integer> preorderTraversal(TreeNode root) {
        /**
            前序遍历属于自顶向下的遍历，递归部分：根结点 左子树 右子树
            递归结束条件：当前结点值为空
            返回值为一个集合，也就是要将结点的元素值添加到集合中

            输出错误分析：
                因为我采用的是递归遍历二叉树，但是没有把递归的算法分离出来，
                这样在没次进入新结点时，都会创建一个新的集合，这样就导致集
                合中只保存了一个值

            PS:
                （1）ArrayList与LinkedList的区别：
                    两者都实现类List接口，但是前者的底层实现原理是数组，
                    后者的实现原理是链表；
                    前者查询速度更快，后者插入删除操作更快；
                    后者每个结点存储两个引用，所以后者更占空间
         */

        //创建一个结合
        ArrayList<Integer> res = new ArrayList<Integer>();

        preorder(root, res);
        
        return res;
    }
}

Java迭代版本:

---

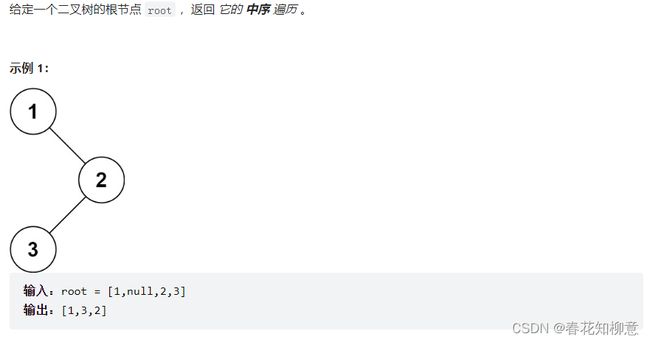
LeetCode 94: 二叉树的中序遍历

⭕️ 解题思路：

大体部分与前序遍历类似，再添加元素到集合中时，先遍历左子树再添加元素即可

❌ Java递归版本:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    //定义一个方法来完成中序遍历
    public void inorder(TreeNode root, ArrayList res){
        
        
        if(root == null){
            return;
        }
        //递归左子树
        inorder(root.left, res);
        //将结点值添加到集合中
        res.add(root.val);
        //递归右子树
        inorder(root.right, res);


    }
    public List<Integer> inorderTraversal(TreeNode root) {
        //创建一个集合
        ArrayList<Integer> res = new ArrayList<Integer>();

        //调用中序遍历的方法
        inorder(root, res);

        return res;
    }
}

---

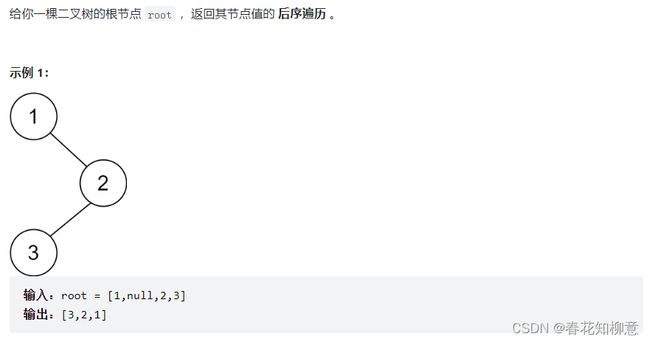
LeetCode 145: 二叉树的后序遍历

️ 解题思路:

与前序和中序类似，最后处理根结点

️ Java递归版本:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }    
 */
class Solution {
    public void postorder(TreeNode root, ArrayList res){
        if(root == null){
            return;
        }
        postorder(root.left,res);
        postorder(root.right, res);     
        res.add(root.val);
    }
    public List<Integer> postorderTraversal(TreeNode root) {
        ArrayList<Integer> res = new ArrayList<Integer>();

        postorder(root, res);

        return res;
    }
}

---

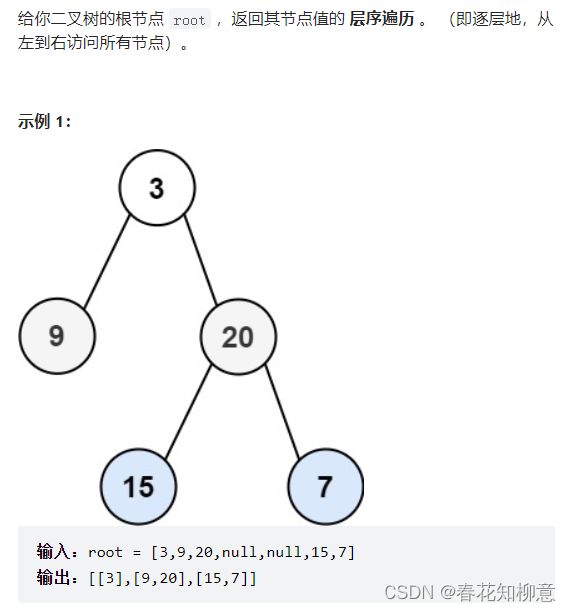
LeetCode 102: 二叉树的层次遍历

解题思路：

（1）通过给出的算法模板我们可以知道，返回的是一个大集合里包含多个小集合。由此我们可以得知，对于每一个子集合存储着每一层的元素。

（2）通过设置索引来为结点找到应该添加到哪个集合中。

（3）对于层次遍历的顺序是从左到右的，所以我们选择先递归左子树再递归右子树

☎️ Java递归版本:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public void level(TreeNode root, int index, List<List<Integer>> result){
        //如果结点为空
        if(root == null){
            return;
        }
        //如果当前集合的大小小于树的深度，说明需要创建一个新的子集合
        if(result.size() < index){
            result.add(new ArrayList<Integer>()); 
        }
        //将当前结点值添加到该层的集合中
        result.get(index - 1).add(root.val);
        //因为层次遍历的顺序是从左向右，所以应该先递归左子树再递归右子树
        if(root.left != null){
            level(root.left, index + 1, result);
        }
        if(root.right != null){
            level(root.right, index + 1, result);
        }

    }
    public List<List<Integer>> levelOrder(TreeNode root) {
        //如果根结点为空，返回指定类型的集合
        if(root == null){
            return new ArrayList<List<Integer>>();
        }
        //创建一个结果集合
        List<List<Integer>> result = new ArrayList<List<Integer>>();
        //调用层序遍历递归算法
        level(root, 1, result);
        //返回
        return result;
    }
}