Motion Plan之带动力学约束路径搜索

Motion Plan之搜索算法笔记
Motion Plan之基于采样的路径规划算法笔记

为什么要动力学规划：

前面几章介绍的路径规划，我们只是认为机器人是质点，这节课要说的就是，如何在考虑机器人的运动学模型下再去找一个安全可行的路径。考虑了机械运动学模型以后，路径规划方法仍然可以分为像前两课一样归为基于搜索的和基于采样的。KINODYNAMIC是运动学和动力学两部分组成的，机器人不是简单的一个质点，可以随意运动的一个质点；它的高阶模型受到一个微分的约束。Kinodynamic Path Finding是一种在机器人和运动规划中的问题类别，其中必须满足速度、加速度和力/扭矩界限，以及如避免障碍物等运动约束。这是一种解决运动规划问题的方法，它考虑了机器人的动力学约束。这意味着，kinodynamic规划算法输出的引导轨迹不仅要对机器人的环境避免碰撞，而且还要对机器人的连续时间动力学的代表模型可行。
传统规划算法生成的路径无法准确匹配机器人的运动约束,使得规划与控制脱节。例如汽车的非完全约束限制其侧方移动,但传统算法可能生成需要急转的最短路径,很难优化成可行解。 尤其是高速运动场景下,初态末态间的精确运动学建模和控制求解至关重要,这需要求解两点边界值问题。 混合A*等算法试图在规划层面加入约束,但仍面临启发函数设计、离散化、连续性等困难,说明了这是一个 layer 上的系统性问题,而不是简单扩展现有方法就能完美解决。 更准确地对运动学建模,直接在规划层面加入约束,不仅能生成更优路径,也能减轻后续轨迹优化负担,改善整体规划控制系统的协同性。由于系统的微分约束，状态对之间的直线连接通常不是有效的轨迹。找到的路径越平滑，优化它就越容易。 综上,动力学规划为使机器人运动更符合自身约束条件、实现更流畅高效的规划与控制提供了可能。与损失函数设计等其他问题一样,这也是实现复杂机器人功能必需解决的基本问题。
总计一下之所以要在Front end阶段就做KINODYNAMIC path find原因如下：

1. 传统规划方法只考虑避障,不能进行平滑运动
2. 实际机器人受运动学约束和动力学约束影响,不是质点模型
3. 必须在规划层面考虑这些约束,生成符合机器人运动能力的路径
4. 这是实现机器人自动控制和功能的基础
5. 使机器人运动更平滑自然,逼近人的运动
6. 减少后端轨迹优化的负担,提高整体规划和控制的协同性
7. 有利于我们理解和建模机器人系统,为更复杂控制算法打基础

前置知识

所谓的动力学建模其实就是在对移动机器人做刚体形状建模，然后利用数学方程对建模出来的移动机器人刚体做动力学的建模。得到一个可以通过调整控制变量向量来控制移动机器人做状态变化的过程。

四旋翼无人机建模

建模流程
各部分介绍
KINODYNAMIC控制数学形式

位置动力学模型

牛顿第二定律
$m\dot{v}^{e}=G{e}+T^{b} $
式中$\dot{v}$, 与G右上角的e代表这是地面坐标系下的向量，T右上角的b代表这是机体坐标系下的向量。由于拉力是由螺旋桨产生的，与四旋翼飞行器固连，故在机体坐标系下表示。
等式两边同时除以m：
${\dot{v}}^e=g^e+\frac{T^b}{m}$
将机体坐标系下的拉力转换到地面坐标系，左乘旋转矩阵即可：
$ot{v}^{e}=g{e}+R_{b}^{e}\frac{T{b}}{m} \$
展开成矩阵形式，其中g与T都是标量，g为重力加速度，T为四个螺旋桨产生的总升力：
[ v ˙ x v ˙ y v ˙ z ] = g [ 0 0 1 ] + 1 m ∗ [ c o s θ c o s ψ ; c o s ψ s i n θ s i n ϕ − s i n ψ c o s ϕ c o s ψ s i n θ c o s ϕ + s i n ψ s i n ϕ c o s θ s i n ψ ; s i n ψ s i n θ s i n ϕ + c o s ψ c o s ϕ s i n ψ s i n θ c o s ϕ − c o s ψ s i n ϕ − s i n θ ; s i n ϕ c o s θ c o s ϕ c o s θ ] ∗ [ 0 0 − T ] \begin{bmatrix} \dot{v}_{x}\\ \dot{v}_{y}\\ \dot{v}_{z} \end{bmatrix}=g\begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}+\frac{1}{m}\ast \begin{bmatrix} cos\theta cos\psi ; cos\psi sin\theta sin\phi-sin\psi cos\phi cos\psi sin\theta cos\phi+sin\psi sin\phi \\ cos\theta sin\psi ; sin\psi sin\theta sin\phi+cos\psi cos\phi sin\psi sin\theta cos\phi-cos\psi sin\phi\\ -sin\theta; sin\phi cos\theta cos\phi cos\theta \end{bmatrix}\ast\begin{bmatrix} 0\\ 0\\ -T \end{bmatrix} ​v˙x​v˙y​v˙z​​ ​=g ​001​ ​+m1​∗ ​cosθcosψ;cosψsinθsinϕ−sinψcosϕcosψsinθcosϕ+sinψsinϕcosθsinψ;sinψsinθsinϕ+cosψcosϕsinψsinθcosϕ−cosψsinϕ−sinθ;sinϕcosθcosϕcosθ​ ​∗ ​00−T​ ​
整理得：
$\left{\begin{array}{l} \dot{v}{x}=-\frac{T}{m}(\cos \psi \sin \theta \cos \phi+\sin \psi \sin \phi) \ \dot{v}{y}=-\frac{T}{m}(\sin \psi \sin \theta \cos \phi-\cos \psi \sin \phi) \ \dot{v}_{z}=g-\frac{T}{m} \cos \phi \cos \theta \end{array}\right. \$

姿态动力学模型

由欧拉方程可得
$J{\dot{\omega }}^b+{\omega }^b\times J{\omega }^b=G_a^b+{\tau }^b$
式中， ${\dot{\omega }}^b$ 表示在机体坐标系下的角速度； $G_a^b$表示陀螺力矩； ${\tau }^b$ 表示螺旋桨在机体轴上产生的力矩 。
角速度
ω b = [ ω x b ω y b ω z b ] = [ p q r ] \boldsymbol{\omega}^{b}=\left[\begin{array}{l} \omega_{x}^b \\ \omega_{y}^b \\ \omega_{z}^b \end{array}\right]=\left[\begin{array}{l} p \\ q \\ r \end{array}\right] ωb= ​ωxb​ωyb​ωzb​​ ​= ​pqr​ ​
陀螺力矩 Ga ：当电机高速旋转的时候，相当于一个陀螺。高速旋转的陀螺是非常稳定的个体，具有保持自身轴向不变的能力
G a = [ G a , ϕ G a , θ G a , ψ ] = [ J 1 q ( ϖ 1 − ϖ 2 + ϖ 3 − ϖ 4 ) J 1 p ( − ϖ 1 + ϖ 2 − ϖ 3 + ϖ 4 ) 0 ] {G}_{\boldsymbol{a}}=\left[\begin{array}{c} G_{a, \phi} \\ G_{a, \theta} \\ G_{a, \psi} \end{array}\right]=\left[\begin{array}{c} J_1 q\left(\varpi_{1}-\varpi_{2}+\varpi_{3}-\varpi_{4}\right) \\ J_1 p\left(-\varpi_{1}+\varpi_{2}-\varpi_{3}+\varpi_{4}\right) \\ 0 \end{array}\right] Ga​= ​Ga,ϕ​Ga,θ​Ga,ψ​​ ​= ​J1​q(ϖ1​−ϖ2​+ϖ3​−ϖ4​)J1​p(−ϖ1​+ϖ2​−ϖ3​+ϖ4​)0​ ​
基于假设1惯性矩阵 J可表示为：
J = [ I x x a m p ; − I x y a m p ; − I x z − I x y a m p ; I y y a m p ; − I y z − I x z a m p ; − I y z a m p ; I z z ] = [ I x x a m p ; a m p ; a m p ; I y y a m p ; a m p ; a m p ; I z z ] \boldsymbol{J}=\left[\begin{array}{rrr} I_{x x} & -I_{x y} & -I_{x z} \\ -I_{x y} & I_{y y} & -I_{y z} \\ -I_{x z} & -I_{y z} & I_{z z} \end{array}\right]=\left[\begin{array}{lll} I_{x x} & & \\ & I_{y y} & \\ & & I_{z z} \end{array}\right] J= ​Ixx​−Ixy​−Ixz​​amp;−Ixy​amp;Iyy​amp;−Iyz​​amp;−Ixz​amp;−Iyz​amp;Izz​​ ​= ​Ixx​​amp;amp;Iyy​amp;​amp;amp;amp;Izz​​ ​
可得：
[ I x x a m p ; a m p ; a m p ; I y y a m p ; a m p ; a m p ; I z z ] [ p ˙ q ˙ r ˙ ] + [ p a m p ; q a m p ; r I x x p a m p ; I y y q a m p ; I z z r i a m p ; j a m p ; k ] = [ J 1 q ( ϖ 1 − ϖ 2 + ϖ 3 − ϖ 4 ) J 1 p ( − ϖ 1 + ϖ 2 − ϖ 3 + ϖ 4 ) 0 ] + [ τ x τ y τ z ] \left[\begin{array}{lll} I_{x x} & & \\ & I_{y y} & \\ & & I_{z z} \end{array}\right]\left[\begin{array}{l} \dot{p} \\ \dot{q} \\ \dot{r} \end{array}\right]+\begin{bmatrix} p & q & r \\ I_{xx}p & I_{yy}q & I_{zz}r\\ i & j & k \end{bmatrix}=\left[\begin{array}{c} J_1 q\left(\varpi_{1}-\varpi_{2}+\varpi_{3}-\varpi_{4}\right) \\ J_1 p\left(-\varpi_{1}+\varpi_{2}-\varpi_{3}+\varpi_{4}\right) \\ 0 \end{array}\right]+\begin{bmatrix} \tau_x\\ \tau_y\\ \tau_z \end{bmatrix} ​Ixx​​amp;amp;Iyy​amp;​amp;amp;amp;Izz​​ ​ ​p˙​q˙​r˙​ ​+ ​pIxx​pi​amp;qamp;Iyy​qamp;j​amp;ramp;Izz​ramp;k​ ​= ​J1​q(ϖ1​−ϖ2​+ϖ3​−ϖ4​)J1​p(−ϖ1​+ϖ2​−ϖ3​+ϖ4​)0​ ​+ ​τx​τy​τz​​ ​
整理得：
$$\{\begin{array}{l}\dot{p}=\frac{1}{I_{xx}}\left[{\tau }_x+qr\left(I_{yy}-I_{zz}\right)-J_{1}q\Omega \right]\\ \dot{q}=\frac{1}{I_{yy}}\left[{\tau }_y+pr\left(I_{zz}-I_{xx}\right)+J_{1}p\Omega \right]\\ \dot{r}=\frac{1}{I_{zz}}\left[{\tau }_z+pq\left(I_{xx}-I_{yy}\right)\right]\end{array}$$

四旋翼飞行器的运动学模型

运动学模型的输入为速度和角速度，输出为位置和姿态
速度与位置的方程：
$$\{\begin{array}{l}{\dot{\mathbf{p}}}^e={\mathbf{v}}^e\\ {\mathbf{p}}^e={\left[\begin{array}{lll}x& amp;y& amp;z\end{array}\right]}^T\\ {\left[\begin{array}{lll}\dot{x}& amp;\dot{y}& amp;\dot{z}\end{array}\right]}^T={\left[\begin{array}{lll}{v}_x& amp;v_y& amp;v_z\end{array}\right]}^T\end{array}$$
姿态角的变化率与机体的旋转角速度有如下关系:
{ Θ ˙ = W ⋅ ω b Θ ˙ = [ ϕ ˙ a m p ; θ ˙ a m p ; ψ ˙ ] T ω b = [ p a m p ; q a m p ; r ] T W = [ 1 a m p ; tan ⁡ θ sin ⁡ ϕ a m p ; tan ⁡ θ cos ⁡ ϕ 0 a m p ; cos ⁡ ϕ a m p ; − sin ⁡ ϕ 0 a m p ; sin ⁡ ϕ / cos ⁡ θ a m p ; cos ⁡ ϕ / cos ⁡ θ ] \left\{\begin{array}{l} \dot{\boldsymbol{\Theta}}=\boldsymbol{W} \cdot \boldsymbol{\omega}^{b} \\ \dot{\boldsymbol{\Theta}}=\left[\begin{array}{lll}\dot{\phi} & \dot{\theta} & \dot{\psi}\end{array}\right]^{T} \\ \omega^b = \left[\begin{array}{lll}p & q & r\end{array}\right]^{T} \\ \boldsymbol{W}=\left[\begin{array}{ccc} 1 & \tan \theta \sin \phi & \tan \theta \cos \phi \\ 0 & \cos \phi & -\sin \phi \\ 0 & \sin \phi / \cos \theta & \cos \phi / \cos \theta \end{array}\right] \end{array}\right. ⎩ ⎨ ⎧​Θ˙=W⋅ωbΘ˙=[ϕ˙​​amp;θ˙​amp;ψ˙​​]Tωb=[p​amp;q​amp;r​]TW= ​100​amp;tanθsinϕamp;cosϕamp;sinϕ/cosθ​amp;tanθcosϕamp;−sinϕamp;cosϕ/cosθ​ ​​
整理可得：
[ ϕ ˙ θ ˙ ψ ˙ ] = [ 1 a m p ; tan ⁡ θ sin ⁡ ϕ a m p ; tan ⁡ θ cos ⁡ ϕ 0 a m p ; cos ⁡ ϕ a m p ; − sin ⁡ ϕ 0 a m p ; sin ⁡ ϕ / cos ⁡ θ a m p ; cos ⁡ ϕ / cos ⁡ θ ] [ p q r ] \left[\begin{array}{l} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{array}\right]=\left[\begin{array}{ccc} 1 & \tan \theta \sin \phi & \tan \theta \cos \phi \\ 0 & \cos \phi & -\sin \phi \\ 0 & \sin \phi / \cos \theta & \cos \phi / \cos \theta \end{array}\right]\left[\begin{array}{l} p \\ q \\ r \end{array}\right] ​ϕ˙​θ˙ψ˙​​ ​= ​100​amp;tanθsinϕamp;cosϕamp;sinϕ/cosθ​amp;tanθcosϕamp;−sinϕamp;cosϕ/cosθ​ ​ ​pqr​ ​

汽车建模

车辆动力学建模是指通过数学模型描述车辆在不同运动和操控情况下的行为。这种建模是车辆动力学控制的基础，能够帮助设计控制系统以优化车辆性能和稳定性。
车辆动力学模型及其控制的数学形式通常通过一系列微分方程来表示，这些方程描述了车辆在运动过程中的各种物理量随时间的演变。
车辆动力学控制的目标是通过调整操纵输入，使车辆达到期望的运动性能。典型的车辆动力学控制系统包括横向和纵向控制。
车辆动力学模型有很多种，以下是一些常见的模型：

1. 单轨模型：这是一种简化的模型，它将车辆视为一个刚体，只考虑车辆的横向运动。这种模型通常用于研究车辆的稳定性和操控性。
2. 双轨模型：这种模型比单轨模型更复杂一些，它将车辆视为两个并行的刚体（左右两侧），可以分别考虑车辆的横向和纵向运动。这种模型可以更准确地模拟车辆的动态行为。
3. 多体模型：这种模型将车辆分解为多个相互连接的刚体（如车身、悬挂系统、轮胎等），每个刚体都有自己的运动方程。这种模型可以模拟车辆的复杂动态行为，如悬挂系统的运动、轮胎的滑动等。
4. 非线性模型：这种模型考虑了车辆动力学中的非线性因素，如轮胎的非线性摩擦特性、悬挂系统的非线性刚度等。这种模型可以更准确地模拟车辆在极限条件下的行为。
5. 自行车模型（Bicycle Model）

首先要简化汽车运动，其中自行车模型就是简单且有效的简化方式。自行车模型基于如下几个假设：
车辆在垂直方向的运动被忽略掉了，也就是说我们描述的车辆是一个二维平面上的运动物体（可以等价与我们是站在天空中的俯视视角）
车辆自行车模型是一种常用的车辆动力学模型，它将车辆简化为一个自行车，只考虑车辆的横向运动和转向运动。这种模型主要用于研究车辆的稳定性和操控性。
在自行车模型中，车辆的运动状态可以由以下几个变量表示：

• 位置：车辆的位置通常由车辆的横向位置和纵向位置表示。
• 速度：车辆的速度通常由车辆的横向速度和纵向速度表示。
• 航向角：航向角是车辆的前进方向与水平方向的夹角。
• 转向角：转向角是车辆前轮与车辆的夹角。

车辆的动力学行为则可以通过以下的微分方程来描述：

• 位置的变化率：位置的变化率等于速度。
• 速度的变化率：速度的变化率等于加速度。
• 航向角的变化率：航向角的变化率等于车辆的转向速度。
• 转向角的变化率：转向角的变化率等于车辆的转向加速度。

其中 θ是其在 Yaw 方向的偏转角度，它是相对于 x 轴的逆时针方向的角度，v 是 θ 方向的速度，L是车辆的轴距（前后轮胎的距离）, (x,y) 是车辆的坐标。
可以通过以下的微分方程来描述：

1. 位置的变化率：位置的变化率等于速度。在二维平面上，我们可以将其分解为x和y两个方向。假设车辆的速度为v，航向角为θ，那么位置的变化率可以表示为：
   • $\frac{dx}{dt}=v.cos(\theta )$
   • $\frac{dy}{dt}=v.sin(\theta )$
2. 速度的变化率：速度的变化率等于加速度。假设车辆的加速度为a，那么速度的变化率可以表示为：
   • $\frac{dv}{dt}=a$
3. 航向角的变化率：航向角的变化率等于车辆的转向速度。假设车辆的转向速度为ω，那么航向角的变化率可以表示为：
   • $\frac{dt}{d\theta }=\omega$

这些方程描述了车辆在给定控制输入（如油门、刹车和转向）下的运动行为。

简化汽车模型

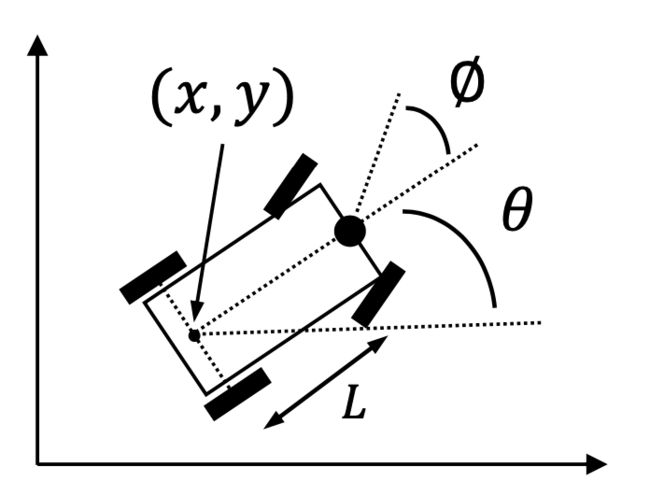
( x . y . θ . ) = ( v c o s θ v s i n θ r L t a n ϕ ) \begin{pmatrix} \stackrel{.}{x} \\ \stackrel{.}{y} \\ \stackrel{.}{\theta} \\ \end{pmatrix} = \begin{pmatrix} v cos\theta\\ vsin\theta \\ \frac{r}{L}tan\phi\\ \end{pmatrix} ​x.y.​θ.​​ ​= ​vcosθvsinθLr​tanϕ​ ​

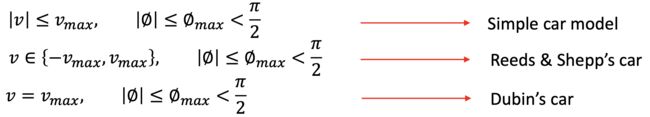
"单轮模型"和"差速驱动模型”

( x . y . θ . ) = ( c o s θ s i n θ 0 ) . v + ( 0 0 1 ) . ω \begin{pmatrix} \stackrel{.}{x} \\ \stackrel{.}{y} \\ \stackrel{.}{\theta} \\ \end{pmatrix} = \begin{pmatrix} cos\theta \\ sin\theta \\ 0 \\ \end{pmatrix}.v + \begin{pmatrix} 0 \\ 0 \\ 1 \\ \end{pmatrix}.\omega ​x.y.​θ.​​ ​= ​cosθsinθ0​ ​.v+ ​001​ ​.ω

( x . y . θ . ) = ( r 2 ( μ l + μ r ) c o s θ r 2 ( μ l + μ r ) s i n θ r L ( μ r − μ l ) ) \begin{pmatrix} \stackrel{.}{x} \\ \stackrel{.}{y} \\ \stackrel{.}{\theta} \\ \end{pmatrix} = \begin{pmatrix} \frac{r}{2}(\mu_l+\mu_r) cos\theta\\ \frac{r}{2}(\mu_l+\mu_r)sin\theta \\ \frac{r}{L}(\mu_r-\mu_l) \\ \end{pmatrix} ​x.y.​θ.​​ ​= ​2r​(μl​+μr​)cosθ2r​(μl​+μr​)sinθLr​(μr​−μl​)​ ​

经过动力学建模得到了一个控制方程，前面几章也介绍了如何把移动机器人当成质点得到了一条质点轨迹路径。那么接下来的事情就是如何把动力学建模得到的控制方程融合到质点轨迹路径中。然后把各种约束融合进代价函数，通过求解代价函数最小化得到符合约束的满足动力学控制要求的轨迹。
那么动力学控制方程融入质点轨迹主流有两种方法：控制离散化、状态离散化。
1.控制离散化就是说我们已经知道动力学控制方程了，那么我们能不能把质点轨迹上每个质点出了坐标信息还带上控制向量信息，控制向量是一个连续的向量不好表示，所以为了更方便求解减少求解空间我们就把控制向量离散化变成有限的可选项。这样可以更方便的写出代价函数，也更容易求解得出代动力学约束的可行解。
2.状态离散，意思就是我们把质点轨迹上每个质点带上移动机器人在这个质点的状态信息。然而状态也是一个连续的向量，解空间大不利于求解。所以我们把状态离散成有限的状态表示，这样在求解时候知道每个质点的状态，求解问题就变成在如何求解状态间转移矩阵符合代价函数最小化问题。
下面章节就会具体介绍如何求解带状态约束的路径问题。

正文

State Lattice Planning

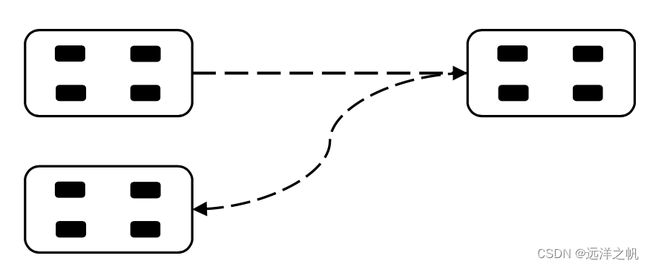
状态栅格，顾名思义就在在普通的栅格化地图的基础上，多加了机器人运动学模型的约束，确保机器人能沿着相邻两点之间生成的路径运动，并且能够具有状态连续性（速度连续等）。

如何构建状态栅格

状态栅格图中，每个顶点的连线都是根据机器人的运动学模型生成的，都是切实可行的路径，而普通栅格 (grid)的方法并没有结合模型。在构建状态栅格图（State Lattice Search）之前，需要对被控对象进行运动学分析，即建立对应的运动学模型。运动学模型主要描述了位置、速度、加速度、转向角度等等状态量在时间上的状态转移，以及对所关心的这些状态量的边界条件进行约束。
从控制空间和状态空间中进行采样，对于机器人模型：′ = (, )
• 机器人是差动驱动的。
• 我们有机器人的初始状态 ₀。
• 对于State Lattice Search，通常有两种采样方式：

基于控制空间（Control Space)的采样：

在已知被控对象的情况下，我们固定输入量u（控制量）与积分时
间T，由此进行前向积分即可得到被控对象从任意初始状态s_{0}过度到的终止状态s_{f}。前向积分的方式能够简单粗暴地对被控对象在任意时间T之后的状态进行预测，从而得到一系列状态集合，这就是在控制空间中的采样。由于输入量u与积分时间T都是任意给定的，因此，基于控制空间的采样往往是没有明确的目的性的，它的采样结果只能分布在某些状态附近，但不能精确地采样到某一个给定状态。

选择一个，固定时间间隔，对系统进行前向模拟（数值积分）。
• 前向模拟
• 固定 ,
• 无任务引导
• 易于实现
• 规划效率较低
具体流程是:
(1)为机器人选择一个初始状态s0。
(2)对控制输入u进行离散抽样,得到一组可行的控制集合{u1, u2,…}。
(3)对每一个控制输入ui,选择一个时间段T,进行前向仿真(numerical integration)获得一个终止状态si。
(4)重复步骤(2)-(3),直到构建完整的状态栅格图。

例子

设无人机机器人状态方程如下如下：
State:  s = ( x y z x ˙ y ˙ z ˙ ) Input:  u = ( x ¨ y ¨ z ¨ ) s ˙ = A ⋅ s + B ⋅ u A = [ 0 a m p ; I 3 a m p ; 0 a m p ; ⋯ a m p ; 0 0 a m p ; 0 a m p ; I 3 a m p ; ⋯ a m p ; 0 ⋮ a m p ; ⋱ a m p ; ⋱ a m p ; ⋱ a m p ; ⋮ 0 a m p ; ⋯ a m p ; ⋯ a m p ; 0 a m p ; I 3 0 a m p ; ⋯ a m p ; ⋯ a m p ; 0 a m p ; 0 ] B = [ 0 0 ⋮ 0 I 1 ] \text{State: }\mathbf{s}={\left(\begin{array}{l}{x}\\ {y}\\ {z}\\ {\dot{x}}\\ {\dot{y}}\\ {\dot{z}}\end{array}\right)} \quad \text{Input: }u=\left(\begin{matrix}{\ddot{x}}\\ {\ddot{y}}\\ {\ddot{z}}\\ \end{matrix}\right)\\ \dot{s}=A\cdot s+B\cdot u \\A=\begin{bmatrix}0&I_3&0&\cdots&0\\ 0&0&I_3&\cdots&0\\ \vdots&\ddots&\ddots&\ddots&\vdots\\ 0&\cdots&\cdots&0&I_3\\ 0&\cdots&\cdots&0&0\end{bmatrix}\quad B=\begin{bmatrix}0\\ 0\\ \vdots\\ 0\\ I_1\end{bmatrix} State: s= ​xyzx˙y˙​z˙​ ​Input: u= ​x¨y¨​z¨​ ​s˙=A⋅s+B⋅uA= ​00⋮00​amp;I3​amp;0amp;⋱amp;⋯amp;⋯​amp;0amp;I3​amp;⋱amp;⋯amp;⋯​amp;⋯amp;⋯amp;⋱amp;0amp;0​amp;0amp;0amp;⋮amp;I3​amp;0​ ​B= ​00⋮0I1​​ ​
固定输入量$\mu$和和时间 T，然后进行前向积分，就可以知道T后的机器人状态。尤其是当机器人是线性系统的时候。在知道T时刻机器人的末状态之后，就可以通过状态转移方程：
$s(t) = e^{{At}s_0+[\int_0}te^{A(t-\sigma)}Bd\sigma]u_m，\$
来还原出过程之中的各个状态，其中矩阵A是状态转移矩阵。假设$t=\tau$，要求解$e^{At}$的求解是一件很麻烦的事，我们可以利用泰勒展开
$e^{{At}=I+\frac{At}{1!}+\frac{(At)}2}{2!}+\frac{(At)^{3}{3!}+\cdots+\frac{(At)}k}{k!}+\cdots \$
A矩阵有一个性质，就是nilpotent，也就是说它在多次方之后会变为0，那高次项就都被消去了，这使得$e^{At}$在(n-1)次矩阵多项式中都具有封闭的表达式，更多的求解方式可参考现代控制理论。

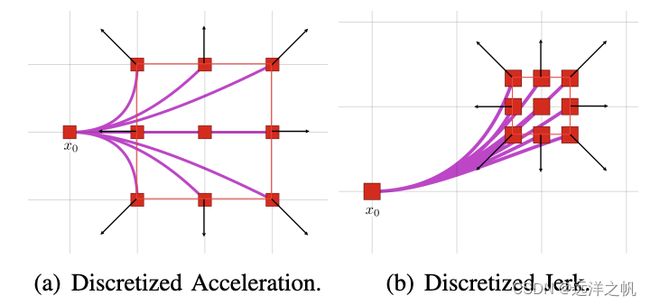
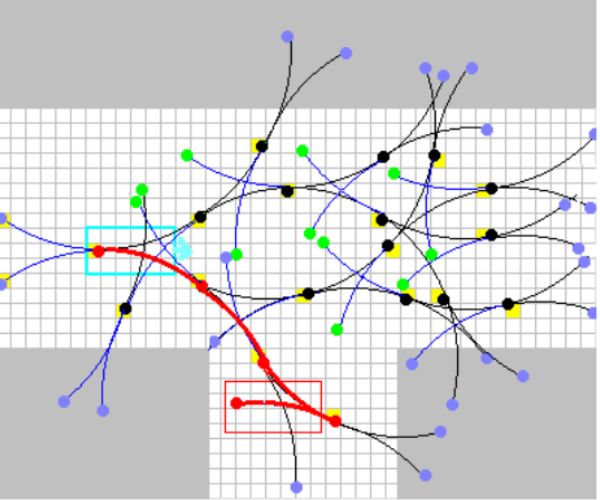
上图展示了从初始状态x0开始的9个平面运动基元的示例。左图是一个受加速度控制（n = 2）的系统，右图是一个受冲量（Jerk）控制（n = 3）的系统。黑箭头指示对应的控制输入。红色边界显示了由控制限制umax引导的终态的可行区域。初始速度和加速度分别为$v_0$= [1, 0, 0]^T和$a_0$ = [0, 1, 0]^T（仅适用于右图）。
通过搜索获得的格子图注意事项：

• 在搜索过程中，可以在需要时再构建图形，节省存储空间和计算时间。
• 当发现新的节点（状态）时，创建节点和边（运动基元）。
• 节省计算时间/空间。

上图表示的是9个离散化示例和25个离散化示例

给一个更宏观的车的例子，可以看到基于控制空间采样的应用
车状态方程：
S t a t e : s = ( x y θ ) I n p i t : μ = ( v ϕ ) S y s t e m e q u a t i o n : ( x . y . θ . ) = ( v c o s θ v s i n θ r L t a n ϕ ) State: s=\begin{pmatrix} {x} \\ {y} \\ {\theta} \\ \end{pmatrix} \\ Inpit: \mu =\begin{pmatrix} {v} \\ {\phi} \\ \end{pmatrix} \\ System equation: \begin{pmatrix} \stackrel{.}{x} \\ \stackrel{.}{y} \\ \stackrel{.}{\theta} \\ \end{pmatrix} = \begin{pmatrix} v cos\theta\\ vsin\theta \\ \frac{r}{L}tan\phi\\ \end{pmatrix} State:s= ​xyθ​ ​Inpit:μ=(vϕ​)Systemequation: ​x.y.​θ.​​ ​= ​vcosθvsinθLr​tanϕ​ ​

对于搜索树中的每一个 ∈ ：

• 选择一个控制向量
• 在短时间内积分方程
• 将无碰撞的运动添加到搜索树中

具体步骤如下：

1. 选择一个 ∈
2. 选择, ∅ 和
3. 从开始积分运动
4. 如果无碰撞，则添加结果

基于状态空间（State Space)的采样¹：

这种采样方式则是在给定被控对象的初始以及目标状态后，反向计算
中间过程。相对于前者，该采样方式在工程上较难实施，我们需要对其进行两点边界值问题的求解，才能求得两个状态之间轨迹¹。两点边界值问题（BVP）经典的两点边界值问题，其实就是多项式方程求系数的过程。然而，求解BVP问题能够求解一条可通行轨迹，却无法求得一条最优轨迹。或者，当其边界条件部分确定时（如位置确定，速度、加速度状态不确定），需要求解OBVP问题。OBVP问题可以认为是一个最优控制问题。对基于状态空间的采样方法而言，求解OBVP问题即可求得任意两点之间符合运动学方程的最优轨迹。

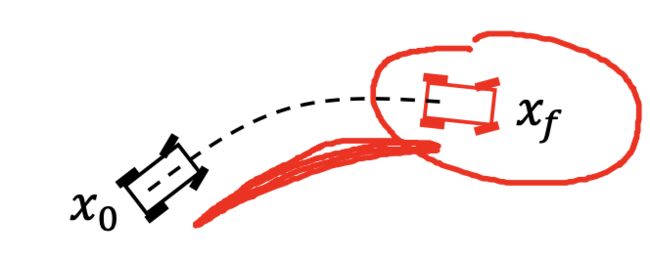
选择一个 ₘ, 找到连接（轨迹）₀和ₘ之间的路径。
• 反向计算
• 需要计算 ,
• 良好的任务引导
• 难以实现
• 高规划效率
具体流程是:
(1) 在状态空间中选择一个初始状态s0。
(2) 对s0的8个邻居状态进行边界值问题(boundary value problem, BVP)求解,找到从s0到邻居状态的可行轨迹。
(3) 以找到的邻居状态为中心,重复步骤(2),向外扩展构建状态栅格图。
总的来说，状态栅格规划器（State Lattice Planner）是一种基于采样的满足动力学约束的路径规划算法³。它通过基于控制空间的采样方式和基于状态空间的采样方式，构建出满足动力学约束的路径¹²。这两种方法各有优缺点，基于控制空间的采样方式实现相对简单，但效率不高；而基于状态空间的采样方式虽然在工程上较难实施，但它使得算法具有启发性和贪心性。

例子

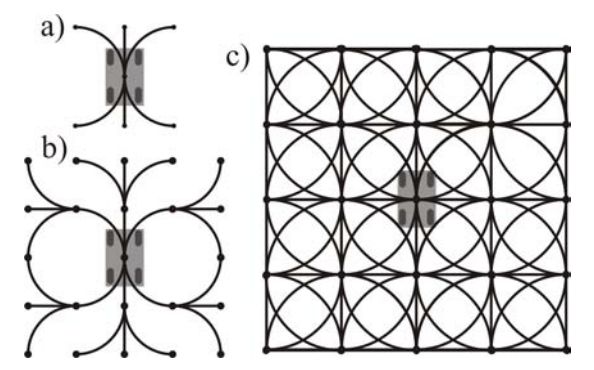
图1：Reeds-Shepp Car的可达性图。显示了可达性图构建的各个阶段。一个有三个动作的特殊离散化的Reeds-Shepp Car可以在工作空间中任意移动。

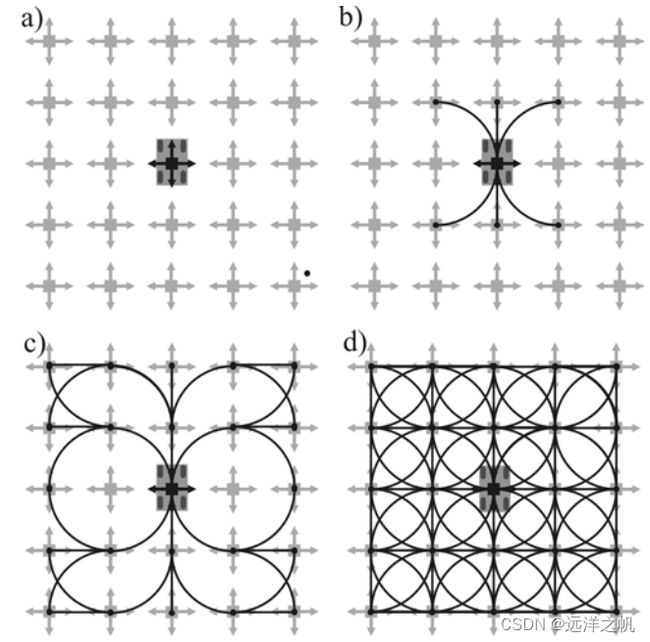
图2：为Reeds-Shepp Car构造格子。在a)中，我们定义了一个C空间的离散化（这里选择了一个网格，箭头表示允许的航向），选择了一个原点；b)对于原点周围的8个邻居节点，找到了可行的路径；c)同样的查询向外扩展到24个邻居，只显示了一些直接的路径；d)完整的格子。
构造状态格子：
图1显示了一个Reeds-Shepp Car的可达性图，它有三个动作，适当地离散化了。随着汽车无限地行驶，图是通过“编译”所有可行的运动而构造的。**然而，状态格子是通过使用逆向路径生成器来找到从网格中的任何一个节点到原点（图2中的黑色方块）的路径而构造的。**在构造格子时选择原点是任意的（因为从任何节点都有相同的运动集合），可以将所有可行的路径复制到格子中的任何节点。在极限情况下，当图1中的图通过Reeds-Shepp car无限长地扩展，而图2中的格子通过包含从原点到任何节点的可行路径（并将所得到的集合复制到所有节点）而构建时，由于表示所有可行的路径，图和格子将是相同的。在不失一般性的情况下，认为状态格子是系统可达性图的有效表示。
离散化：
离散化将运动规划问题转化为一个顺序决策过程。采用典型的策略，假设只在离散状态下做出决策。状态是格子中的节点，连接状态的运动是边。格子中的每个节点代表一个4维姿态，包括2D位置、航向和曲率。这种表示使得格子能够足够通用，满足汽车的典型非完整约束和完整约束。假设位置被离散化为分隔的矩形网格，任何有用的航向离散化都是可接受的。现在假设均匀地划分区间，对于在区间中离散化曲率，也是如此，其中是最大曲率，是最小转弯半径的倒数，用与相同的长度单位表示。
离散化的规则性：
如果离散化具有一定程度的规则性，那么两个给定状态之间的空间关系会由于存在其他相同排列的状态对而经常重复。具有一定程度规则性的离散化导致了一组类似的运动选项。
状态格点的构造：
假设状态空间离散化在至少平移坐标上是规则的。具体来说，如果两个姿态之间的路径是可行的，那么对于任意整数值，另一个路径也是可行的。虽然这两种运动的起始和终止状态是不同的，但运动本身（可能以转向函数编码）是相同的。事实上，现在只考虑从原点发出的运动集合。只需要显式地表示这个规范集合。通过在任何其他节点重复这个表示，就可以得到整个格点（图2b）。

车辆在多个可行离散状态空间采样，两层示例图

• 两层格子图：只有第一层不同，因为不同的初始状态。
• 不同的初始状态：指的是系统从不同的位置、航向和曲率开始运动。这会影响格子图中的节点和边的分布和连接。

状态空间采样和控制空间采样是两种生成状态格子的方法，它们的差异和优缺点如下：

• 状态空间采样是一种从状态空间中采样配置，然后用可行路径连接它们的方法。这种方法的优点是可以保证状态格子的完备性，即任何可行的运动都可以在状态格子中找到。利用逆向路径生成器（inverse path generator）来找到从任意节点到目标节点的可行路径，然后将这些路径作为状态格子的边。缺点是需要解决逆运动规划问题，即给定起始和终止配置，找到一条可行路径。这种方法的难点是如何高效地解决逆向路径生成问题，即如何在有限的时间内找到一条满足运动约束、最小化某个代价函数、并且终止于离散状态的路径。通常需要使用数值方法或者近似方法，可能会导致计算开销大或者解的质量低³
• 控制空间采样是一种从控制空间中采样控制输入，然后用它们生成一组基本运动（motion primitives），并将它们连接到状态格子中的方法。利用一组预先定义的基本运动（motion primitives）来构造状态格子的边。这些基本运动是由一些常量或者多项式控制输入产生的，可以用解析的方式表示。这种方法的优点是可以避免逆运动规划问题，而且可以根据不同的优化准则设计基本运动。缺点是需要保证基本运动的覆盖性，即任何可行的运动都可以由基本运动的组合来近似。这种方法的难点是如何设计基本运动的集合，使得它们能够覆盖所有可能的运动方向，同时又能够满足一些优化标准，例如最小化曲率变化、最大化直线运动等。这个问题通常需要精心地设计控制空间的离散化和基本运动的生成算法²。通常需要根据具体的运动模型和应用场景进行调整和优化。

求解

开始求解之前其实你应该问问自己为什么一个采样器需要去求解一个状态转移方程问题呢？其实原因很简单，如果有解就意味着状态采样点是可达的也就说这个点是有效的。
上面章节介绍了“基于状态空间采样”的采样点的生成流程，里面有一个问题就是知道了起始、终止点的状态（位置坐标、动力学模型参数向量）如何求解状态转移方程。这个章节主要就是介绍如何求解状态转移方程，会涉及到边界值求解知识。

• 边值问题（BVP）：BVP是状态采样格子规划的基础。
• 没有通用的解决方案：BVP需要根据具体情况进行设计。
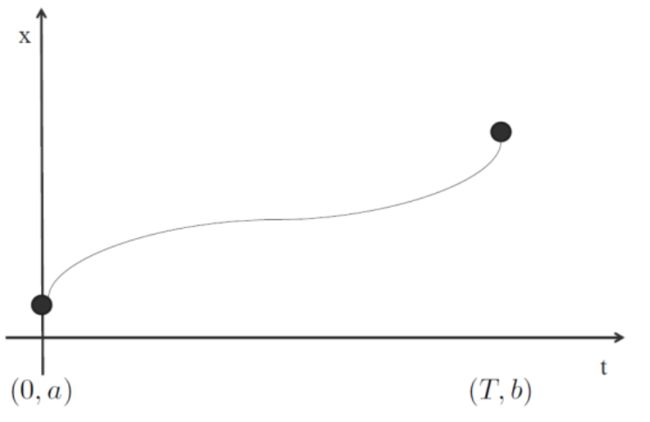
• 通常涉及复杂的数值优化：BVP需要设计一条轨迹 ，使得：
  • (0) =
  • (T) =

如何对求解问题建模

• 用5阶多项式来表示轨迹：
  _ = _5^5 + _4^4 + _3^3 + 2_^2 + _1 + _0

• 边界条件
  | | 位置 | 速度 | 加速度 |
  | — | — | — | — |
  | t = 0 | a | 0 | 0 |
  | t = T | b | 0 | 0 |

• 轨迹表示方程

[ a b 0 0 0 0 ] = [ 0 0 0 0 0 1 T 5 T 4 T 3 T 2 T 1 0 0 0 0 1 0 5 T 4 4 T 3 3 T 2 T 2 1 1 0 0 0 0 2 0 0 20 T 3 12 T 2 6 T 1 2 0 0 ] [ c 5 c 4 c 3 c 2 c 1 c 0 ] \begin{bmatrix}a\\b \\ 0\\ 0\\0\\0 \end{bmatrix} = \begin{bmatrix}0&0&0&0&0&1\\T^5&T^4&T^3&T^2&T&1\\ 0&0&0&0&1&0\\ 5T^4&4T^3&3T^2&T2^1&1&0\\0&0&0&2&0&0\\20T^3&12T^2&6T^1&2&0&0 \end{bmatrix} \begin{bmatrix}c_5\\c_4 \\ c_3\\ c_2\\c_1\\c_0 \end{bmatrix} ​ab0000​ ​= ​0T505T4020T3​0T404T3012T2​0T303T206T1​0T20T2122​0T1100​110000​ ​ ​c5​c4​c3​c2​c1​c0​​ ​

• 针对约束条件建模最优化求解方程

BVP问题中加入一个优化目标，确保生成成的状态曲线更加符合的工程实践，比如定一个Objective，要使得加速度的平方和最小，状态转移的过程要尽可能的快，如下所示：
$J={\int }_0^{T}g(x,u)dt={\int }_0^T(1+u^{T}Ru)dt={\int }_0^T(1+a_x^2+a_y^2+a_z^2)dt$
状态量，输入量和系统方程表征如下：
x = ( p x p y p z v x v x v z ) , u = ( a x a y a z ) , x ˙ = f ( x , u ) = ( v x v y v z a x a y a z ) x=\begin{pmatrix}p_x\\ p_y\\ p_z \\ v_x\\ v_x\\ v_z\end{pmatrix},u=\begin{pmatrix}a_x\\ a_y\\ a_z\end{pmatrix},\dot x=f(x,u)=\begin{pmatrix}v_x\\ v_y \\ v_z\\ a_x\\ a_y\\ a_z\end{pmatrix} x= ​px​py​pz​vx​vx​vz​​ ​,u= ​ax​ay​az​​ ​,x˙=f(x,u)= ​vx​vy​vz​ax​ay​az​​ ​
边界条件表征如下
i n i t i a l   s t a t e : x ( 0 ) = ( p x 0 p y 0 p z 0 v x 0 v y 0 v z 0 ) , e n d   s t a t e : x ( T ) = ( p x f p y f p z f ? ? ? ) i n i t i a l~s t a t e:x(0)=\left(\begin{matrix}p_{x0}\\ p_{y0}\\ p_{z0}\\ v_{x0}\\ v_{y0}\\ v_{z0}\end{matrix}\right),end~state :x(T) = \left(\begin{matrix}p_{xf}\\ p_{yf}\\ p_{zf}\\ ? \\ ?\\ ?\end{matrix}\right) initial state:x(0)= ​px0​py0​pz0​vx0​vy0​vz0​​ ​,end state:x(T)= ​pxf​pyf​pzf​???​ ​

如何对问题求解

最优边值问题（OBVP）问题求解中的Pontryagin’s minimum principle是一种间接法，可以用来求解有约束的最优控制问题。

• Pontryagin’s minimum principle的基本思想是引入一个共轭变量（或者说伴随变量），构造一个哈密顿函数，然后利用必要的最优性条件，将原问题转化为一个边值问题，再用数值方法求解。
• Pontryagin’s minimum principle的一般形式如下：

假设有一个最优控制问题，目标是最小化一个积分型的性能指标：
${\min }_{u}J(u)={\int }_{t_0}^{t_f}{f}_0(x(t),u(t),t)dt$
其中，$x(t)$是状态变量，$u(t)$是控制变量，$f_0$是给定的函数。同时，需要满足状态方程和边界条件：
$\dot{x}(t)=f(x(t),u(t),t),x(t_0)=x_0,x(t_f)=x_f$
其中，$f$是给定的函数，$x_0$和$x_f$是给定的常数。另外，还有控制约束：
$u(t)\in U,\forall t\in [t_0,t_f]$
其中，$U$是给定的控制集合，通常是一个闭凸集。
Pontryagin’s minimum principle给出了这个问题的一个必要条件，即存在一个共轭变量$\lambda (t)$，使得以下条件成立：

• 共轭方程：$\dot{\lambda }(t)=-\frac{\partial H}{\partial x}(x^{\ast }(t),u^{\ast }(t),\lambda (t),t)$
• 最小值原理：$H(x^{\ast }(t),u^{\ast }(t),\lambda (t),t)={\min }_{u\in U}H(x^{\ast }(t),u,\lambda (t),t)$
• 边界条件：$\lambda (t_f)=\frac{\partial f_0}{\partial x}(x^{\ast }(t_f),u^{\ast }(t_f),t_f)$
• 非平凡性：$\lambda (t)\ne 0,\forall t\in [t_0,t_f]$

其中，$H$是哈密顿函数，定义为：
$H(x,u,\lambda ,t)=f_0(x,u,t)+{\lambda }^{T}f(x,u,t)$
其中，$x^{\ast }(t)$和$u^{\ast }(t)$是最优状态和控制，${\lambda }^T$是$\lambda$的转置。

• Pontryagin’s minimum principle的应用步骤如下²：
  • 根据原问题，构造哈密顿函数$H$。
  • 根据共轭方程，求解$\lambda (t)$的微分方程。
  • 根据最小值原理，求解$u^{\ast }(t)$的表达式。
  • 将$u^{\ast }(t)$代入状态方程，求解$x^{\ast }(t)$的微分方程。
  • 根据边界条件，求解初始共轭变量$\lambda (t_0)$的值。
  • 回代求解最优状态和控制$x^{\ast }(t)$和$u^{\ast }(t)$的值。
• Pontryagin’s minimum principle的优点是可以处理一般形式的最优控制问题，而不需要假设控制变量是可微的或者有界的。它也可以推广到多阶段、多目标、无穷维等复杂情况。缺点是它只给出了一个必要条件，而不是充分条件，所以可能存在多个候选解，需要进一步检验。它也需要求解一个非线性的边值问题，这可能涉及复杂的数值方法。

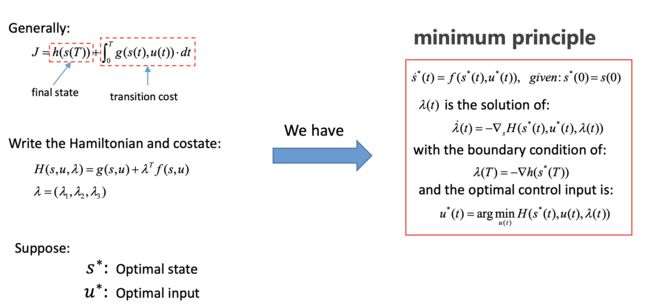
Generally中的$h(s(T))$是一种软约束，可以看成一种罚函数，简单来说就是越趋近于期望状态的时候，值就越小。但因为此处表示的是状态变量的软约束，所以如若固定了终末时间机器人的所有状态，则除了目标状态的$h(s(T))=0$之外，其它情况下都为无穷，会导致极小值原理中的$\lambda (T)=-\nabla h(s^{\ast }(T))$在T处不可导。如果只固定某一些状态量，比如只固定位置，那么边界条件则又恢复了可导性。
Pontryagin’s minimum principle的详细解释应用步骤

• 第一步，根据原问题，构造哈密顿函数$H$。哈密顿函数是一个关于状态变量$x$，控制变量$u$，共轭变量$\lambda$和时间$t$的函数，它的定义为：

$H(x,u,\lambda ,t)=f_0(x,u,t)+{\lambda }^{T}f(x,u,t)$
其中，$f_0$是原问题中的性能指标函数，$f$是原问题中的状态方程函数，${\lambda }^T$是$\lambda$的转置。哈密顿函数的作用是将原问题中的积分型的目标函数转化为一个点型的函数，便于求解。

• 第二步，根据共轭方程，求解$\lambda (t)$的微分方程。共轭方程是一个关于$\lambda$的一阶微分方程，它的形式为：

$\dot{\lambda }(t)=-\frac{\partial H}{\partial x}(x^{\ast }(t),u^{\ast }(t),\lambda (t),t)$
其中，$\dot{\lambda }$表示$\lambda$对$t$的导数，$\frac{\partial H}{\partial x}$表示$H$对$x$的偏导数，$x^{\ast }(t)$和$u^{\ast }(t)$是最优状态和控制。共轭方程的作用是将原问题中的状态变量和控制变量之间的关系转化为共轭变量和状态变量之间的关系，便于求解。

• 第三步，根据最小值原理，求解$u^{\ast }(t)$的表达式。最小值原理是一个关于$u$的最优性条件，它的形式为：

$H(x^{\ast }(t),u^{\ast }(t),\lambda (t),t)={\min }_{u\in U}H(x^{\ast }(t),u,\lambda (t),t)$
其中，$U$是原问题中的控制约束集合。最小值原理的作用是将原问题中的积分型的目标函数转化为一个极值问题，便于求解。

• 第四步，将$u^{\ast }(t)$代入状态方程，求解$x^{\ast }(t)$的微分方程。状态方程是一个关于$x$的一阶微分方程，它的形式为：

$\dot{x}(t)=f(x(t),u(t),t)$
其中，$\dot{x}$表示$x$对$t$的导数。状态方程的作用是描述系统的动态行为，便于求解。

• 第五步，根据边界条件，求解初始共轭变量$\lambda (t_0)$的值。边界条件是一个关于$\lambda$的代数方程，它的形式为：

$\lambda (t_f)=\frac{\partial f_0}{\partial x}(x^{\ast }(t_f),u^{\ast }(t_f),t_f)$
其中，$\frac{\partial f_0}{\partial x}$表示$f_0$对$x$的偏导数，$t_f$是终止时间。边界条件的作用是确定共轭变量的初始值，便于求解。

• 第六步，回代求解最优状态和控制$x^{\ast }(t)$和$u^{\ast }(t)$的值。这一步是将前面求得的$\lambda (t_0)$，$u^{\ast }(t)$和$x^{\ast }(t)$的表达式或数值代入，得到最优解的具体形式或数值。这一步的作用是得到原问题的最优解，便于分析和应用。

对于前面章节建模的最优化方程，写出哈密顿函数：
KaTeX parse error: {align} can be used only in display mode.
其中$\lambda =({\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4,{\lambda }_5,{\lambda }_6{)}^T$为协态向量(costate)，系统模型有多少个状态变量，就有多少个协态。
当状态量和控制量都为最优时，$\mathbf{\lambda }(t)$是汉密顿函数的负梯度，求解微分方程可以得到 $\dot{\mathbf{\lambda }}$以及$\mathbf{\lambda }(t)$。
$\dot{\lambda}=-\nabla H(x^*,u,\lambda)=(0\quad0\quad0\quad-\lambda_1\quad-\lambda_2\quad-\lambda_3)^T \$
λ ( t ) = ( 2 α 1 2 α 2 2 α 3 − 2 α 1 t − 2 β 1 − 2 α 2 t − 2 β 2 − 2 α 3 t − 2 β 3 ) \lambda(t)=\begin{pmatrix}2\alpha_1\\ 2\alpha_2\\ 2\alpha_3\\ -2\alpha_1t-2\beta_1\\ -2\alpha_2t-2\beta_2\\ -2\alpha_3t-2\beta_3\end{pmatrix} λ(t)= ​2α1​2α2​2α3​−2α1​t−2β1​−2α2​t−2β2​−2α3​t−2β3​​ ​
当状态量为最优$x^{\ast }$时，使得汉密顿函数取最小时候的控制量即是我们的最优控制输入${\mu }^{\ast }$。
$u^{*=\arg\min\limits_{u(t)}H(x}(t),u(t),\lambda(t))=\begin{pmatrix}\alpha_1t + \beta_1\ \alpha_2t + \beta_2\ \alpha_3t + \beta_3\end{pmatrix} \$
通过两次前向积分, 得到最优的状态量$x^{\ast }(t)$为
x ∗ = ( 1 6 α 1 t 3 + 1 2 β 1 t 2 + v x 0 t + p x 0 1 6 α 2 t 3 + 1 2 β 2 t 2 + v y 0 t + p y 0 1 6 α 3 t 3 + 1 2 β 3 t 2 + v z 0 t + p z 0 1 2 α 1 t 2 + β 1 t + v x 0 1 2 α 2 t 2 + β 2 t + v y 0 1 2 α 3 t 2 + β 3 t + v z 0 ) , x^{*}=\left(\begin{array}{c}\frac{1}{6} \alpha_{1} t^{3}+\frac{1}{2} \beta_{1} t^{2}+v_{x 0} t+p_{x 0} \\\frac{1}{6} \alpha_{2} t^{3}+\frac{1}{2} \beta_{2} t^{2}+v_{y 0} t+p_{y 0} \\\frac{1}{6} \alpha_{3} t^{3}+\frac{1}{2} \beta_{3} t^{2}+v_{z 0} t+p_{z 0} \\\frac{1}{2} \alpha_{1} t^{2}+\beta_{1} t+v_{x 0} \\\frac{1}{2} \alpha_{2} t^{2}+\beta_{2} t+v_{y 0} \\\frac{1}{2} \alpha_{3} t^{2}+\beta_{3} t+v_{z 0}\end{array}\right), x∗= ​61​α1​t3+21​β1​t2+vx0​t+px0​61​α2​t3+21​β2​t2+vy0​t+py0​61​α3​t3+21​β3​t2+vz0​t+pz0​21​α1​t2+β1​t+vx0​21​α2​t2+β2​t+vy0​21​α3​t2+β3​t+vz0​​ ​,
在极小值原理中，有边界条件如下：
$\lambda (T)=-\nabla h(x^{\ast }(T))$
因为末端速度这个维度未制定,因此$h(x^{\ast }(T))$显然和变量$v$没什么关系，因此求导为 0，
( λ 4 ( T ) λ 5 ( T ) λ 6 ( T ) ) = ( − 2 α 1 T − 2 β 1 − 2 α 2 T − 2 β 2 − 2 α 3 T − 2 β 3 ) = 0 \begin{pmatrix} \lambda_4(T)\\ \lambda_5(T)\\ \lambda_6(T)\end{pmatrix}=\begin{pmatrix} -2\alpha_1T-2\beta_1\\ -2\alpha_2T-2\beta_2\\ -2\alpha_3T-2\beta_3\end{pmatrix}=\boldsymbol{0} ​λ4​(T)λ5​(T)λ6​(T)​ ​= ​−2α1​T−2β1​−2α2​T−2β2​−2α3​T−2β3​​ ​=0
所以我们可以得到一个新的 $\lambda (t)$:
$\mathbf{\beta }=-\mathbf{\alpha }T$
然后我们再利用终末条件$X(T)$来求解得到 $\alpha$:
$\mathbf{\alpha }=-\frac{3({\mathbf{P}}_{\mathbf{f}}-{\mathbf{P}}_0-{\mathbf{v}}_{0}T)}{T^3}=-\frac{3\Delta \mathbf{P}}{T^3},$
其中$P_f$是末端的位置状态, $P_0$和$v_0$是起始的位置状态和速度状态. 所以我们得到最优的控制输入为${\mu }^{\ast }$:
KaTeX parse error: {align} can be used only in display mode.

其中${\Vert \mathbf{\Delta }\mathbf{P}\Vert }^2=\Delta P_x^2+\Delta P_y^2+\Delta P_z^2$
J和 T 无关. 如果想要得到 J的最小值，需要 J 的导数为0。
$T^4+(2V_{0x}\Delta P_x+2V_{0y}\Delta P_y+2V_{0z}\Delta P_z)(9{\Vert \mathbf{\Delta }\mathbf{P}\Vert }^2)=0$
到这边我们就已经可以求解出每个状态采样点的状态参数，也就是我们可以得到每个采样点的具体状态参数了，每个点都是确定了。换一句话说就是我们废了这么多力气到这个章节就是解决了State Lattice的建图过程，下面章节要介绍的就是如何在图上做路径搜索。

状态栅格图上进行图搜索

图已经有了，接下来的问题是我们要如何从图中得到想要的路径规划。前面几篇文章介绍的方法在这边是否还可以用呢？答案是肯定的，只是需要根据现在问题做个适配求解。

• 单层格子规划是一种常用的局部避障方案。
• 不需要图搜索，只需要轨迹选择。
• 根据一个多项代价函数（碰撞风险，信息获取，舒适度，能量，……）对每条轨迹进行评分。

混合A*控制空间检索

• 如果要在线生成密集的动力学格点网格花费太多时间。
• 如何剪枝一些节点呢？局部点选择、根据下一节点走势做减枝、每个节点只算前2步…
• 定义一个剪枝规则：使用网格地图。

具体代码流程如下

• Maintain a priority queue to store all the nodes to be expanded
• The heuristic function h(n) for all nodes are pre-defined
• The priority queue is initialized with the start state XS
• Assign g(XS)=0, and g(n)=infinite for all other nodes in the graph
• Loop
    • If the queue is empty, return FALSE; break;
    #n(n)Choose a proper heuristic according to previous slides
    • Remove the node “n” with the lowest f(n)=g(n)+h(n) from the priority queue
    • Mark node “n” as expanded
    • If the node “n” is the goal state, return TRUE; break;
    #neighbors Find neighbors by forward integrating the state in the node.
    • For all unexpanded neighbors “m” of node “n”
        • If g(m) = infinite
            • g(m)= g(n) + Cnm
            • Push node “m” into the queue
            #add Record the state inside node “m”
        • If g(m) > g(n) + Cnm
            • g(m)= g(n) + Cnm
            #add Update the state inside node “m”
    • end
• End Loop

RRT*搜索路径

RRT算法和带动力学约束的路径生成RRT得差异：

带动力学约束的路径生成如何采样：

LTI（线性时不变）系统状态空间方程：
$\mathbf{x}(t)=\mathbf{Ax}(t)+\mathbf{Bu}(t)+\mathbf{c}$
例如，对于双重积分器系统：
$\mathbf{x}=\left[\begin{array}{c}p\\ v\end{array}\right],\mathbf{A}=\left[\begin{array}{cc}0& \mathbf{I}\\ 0& 0\end{array}\right],\mathbf{B}=\left[\begin{array}{c}0\\ \mathbf{I}\end{array}\right]$
与类似 RRT（快速随机树）在欧几里得空间中采样不同，这要求在完整的状态空间中进行采样。

如何寻找近临点：

如果没有运动约束，可以使用欧几里得距离或曼哈顿距离。在具有运动约束的状态空间中，引入最优控制。
如果引入最优控制，我们可以定义从一个状态转移到另一个状态的成本函数。通常采用的是时间-能量最优的二次形式：
$c(\pi )={\int }_0^{\tau }\left(1+u(t{)}^{T}Ru(t)\right)dt$
其中，$c(\pi )$是成本函数，$\pi$表示路径，$u(t)$表示在时间$t$处的控制输入，$\tau$是路径的时间长度，$R$是权重矩阵。这个成本函数采用了时间和能量的二次形式，对路径进行评估，希望找到最小成本的路径。
如果从一个状态转移到另一个状态的成本较小，那么这两个状态就是接近的。（请注意，如果反向转移，成本可能会不同。）
如果我们知道到达时间 $\tau$和状态转移的控制策略 $u(t)$，我们就可以计算成本。值得庆幸的是，这一切都包含在经典最优控制解决方案中（OBVP）。

无界最优控制解决方案

1. 固定最终状态$x_1$，固定最终时间$\tau$
   $u_t^{\ast }=R^{-1}{B}^T{e}^{A^T(\tau -t)}G(\tau {)}^{-1}(x_1-e^{A\tau }{x}_0)$
   而$x_t$描述如果没有施加控制输入，状态$x$在时间$t$会是什么：
   $x_t=e^{At}{x}_0-{\int }_0^t{e}^{A(t-t^{\prime })}\theta x_{t^{\prime }}d{t}^{\prime }$
   这是微分方程的解：
   ${\dot{x}}_t=A\theta x_t+c,\theta x_0=x_0$
   固定最终状态$x_1$，自由最终时间$\tau$
   如果我们想要找到最优到达时间$\tau$，可以通过将最优控制策略$u_t^{\ast }$带入成本函数$c_{\pi }$并计算积分来实现：
   $c_{\tau }=\tau +[x_1-\theta x_{\tau }{]}^T{G}_{t-1}[x_1-\theta x_{\tau }]$
   通过对$c_{\tau }$关于$\tau$ 求导，可以找到最优的到达时间：
   $\frac{d{c}_{\tau }}{d\tau }=1-2(A{x}_1+c{)}^T{d}_{\tau }-d_{\tau }^{T}B{R}^{-1}{B}^T{d}_{\tau }$
   其中，
   $d_{\tau }=G_{t-1}[x_1-\theta x_{\tau }]$
2. 固定最终状态$x_1$，自由最终时间$\tau$
   解方程$\frac{d{c}_{\tau }}{d\tau }=0$得到${\tau }^{\ast }$。
   需要注意的是，函数$c_{\tau }$可能具有多个局部最小值。对于一个双重积分器系统，它是一个4次多项式。
   给定上述定义的最优到达时间${\tau }^{\ast }$，问题再次转变为一个固定最终状态，固定最终时间的问题。

如何选择父节点

现在，如果我们从随机状态进行采样，我们可以计算控制策略和从树中的那些状态节点到采样状态的成本。选择一个具有最小成本的节点，并检查 $x(t)$和$u(t)$是否在边界内。如果找不到合格的父节点，则重新对状态进行采样。

如何有效地找到附近的节点

每次我们从随机状态x_rand进行采样时，都需要检查树中的每个节点以找到其父节点，这相当于为每个节点解决一个 OBVP（最优边值问题），这样效率不高。
如果我们设置一个成本容忍度$(\rho )$，实际上可以计算状态的边界（前向可达集）可通过x_rand_到达，以及状态的边界（后向可达集）可以以小于_$(\rho )$_的成本到达x_rand。

如果我们以 kd-tree 的形式存储节点，我们可以在树中进行范围查询。
$c_{\tau }=\tau +[x_1-\theta x_{\tau }{]}^T{G}_{t-1}[x_1-\theta x_{\tau }]$
这个公式描述了从状态${\mathbf{x}}_0$转移到状态${\mathbf{x}}_1$的成本随到达时间$\tau$的变化。我们可以看到，给定初始状态${\mathbf{x}}_0$、成本容忍度$\rho$和到达时间$\tau$，${\mathbf{x}}_0$的前向可达集为：
$$\begin{gathered} {\mathbf{x}}_1|\tau +{\mathbf{x}}_1-\theta {\mathbf{x}}_{\tau }{)}^T{G}_{t-1}({\mathbf{x}}_1-\theta {\mathbf{x}}_{\tau })<\rho \\ ={\mathbf{x}}_1|({\mathbf{x}}_1-\theta {\mathbf{x}}_{\tau }{)}^T{G}_{t-1}(\rho -\tau )({\mathbf{x}}_1-\theta {\mathbf{x}}_{\tau })<1 \\ =\mathcal{E}(\theta {\mathbf{x}}_{\tau },G_t(\rho -\tau )) \end{gathered}$$
其中,$\mathcal{E}(\mathbf{x},\mathbf{M})$是以中心$\mathbf{x}$和正定权重矩阵$\mathbf{M}$定义的椭球，形式上定义为：
$\mathcal{E}(\mathbf{x},\mathbf{M})=\{{\mathbf{x}}^{\prime }|{\mathbf{x}}^{\prime T}{\mathbf{M}}^{-1}({\mathbf{x}}^{\prime }-\mathbf{x})<1\}$
因此，前向可达集是所有可能到达时间$\tau$的高维椭球的并集。
为了简化，我们对若干个 (\tau) 进行采样，并计算每个 (\tau) 对应的椭球的轴对齐边界框，并更新每个维度中的最大和最小值：

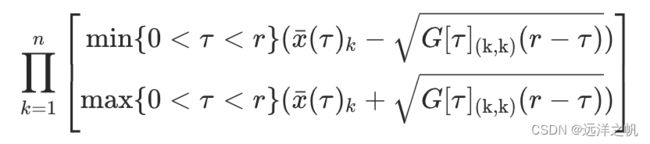
类似地，对于反向可达集的计算。
在进行“Near”查询和“ChooseParent”时，可以从状态的反向可达集中找到${\mathbf{x}}_{\text{near}}$。

如何进行“Rewire”

在进行“Rewire”时，我们计算状态${\mathbf{x}}_{\text{rand}}$的前向可达集，并解决 OBVPs（最优边值问题）。

绿色曲线不考虑障碍物；
红色曲线是运动动力学轨迹规划器的结果；
蓝色曲线是运动动力学轨迹规划器找到的第一条可行轨迹；
黄色线是每个控制点处的控制输入。

小结

本文求解过程引入了动力学约束。从质点模型到引入动力学约束来求解可行路径，是为了在后续求解中可以把不符合实体移动机器人动力学可行解过滤加速back end的求解。
文章从移动机器人建模开始，介绍了四旋翼、车辆的几种简单建模方法。这部分资料是属于控制系统线性、非线性求解部分工作。
接着介绍了如何基于动力学约束来建图，介绍了基于控制空间采样、基于状态空间采样两大类方法。详细的介绍了基于状态空间采样的建模和求解过程，这部分求解过程涉及比较多的数学和物理模型有些难度可以多看几遍；这边需要回答的一个问题是为什么要对状态转移矩阵求解，一言概之就是如果有解那么代表有可达解，符合采样要求可以留下。
基于采样得到图后，接下来的问题就是如何来得到可行路径。这部分介绍的就是如何从构建图中找到可行路径，包括图搜索方法的改造、RRT搜索树的改造和求解流程。