链表【3】
文章目录
- 23. 合并 K 个升序链表
- 题目
- 算法原理
- 代码实现
- 25. K 个一组翻转链表
- 题目
- 算法原理
- 代码实现
23. 合并 K 个升序链表
题目
题目链接:23. 合并 K 个升序链表
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
示例 2:
输入:lists = []
输出:[]
示例 3:
输入:lists = [[]]
输出:[]
提示:
k == lists.length0 <= k <= 10^40 <= lists[i].length <= 500-10^4 <= lists[i][j] <= 10^4lists[i]按 升序 排列lists[i].length的总和不超过10^4
算法原理
解法一:优先级队列(小根堆)
这里用优先级队列,先将k个链表的头节点全部放入这个小根堆当中,然后每次取出对顶元素插入到新链表当中,插入完毕之后,再将这个节点的下一个节点加入到小根堆当中。
时间复杂度:O(nk*logK)
堆向下调整的时间复杂度为O(logN),有
k个链表,每个链表有n,所以复杂度为O(nk*logK)
解法二:分治(递归)
用归并排序的思路,归并排序将数组两两拆分再合并,而这里只是将链表拆分再合并。
直接看图,将递归看作黑盒,不管怎么样,它一定能完成我们要求的任务
时间复杂度:O(nk*logK)
这里将链表两两拆分,就和二叉树一样,每层执行一次合并操作,相当于合并树的高度次,也就是logK,这里有
k个链表,每个链表n个节点,所以复杂度为O(nk*logK)
代码实现
解法一:优先级队列
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
struct cmp
{
bool operator()(const ListNode* l1 , const ListNode* l2)
{
return l1->val > l2->val;
}
};
ListNode* mergeKLists(vector<ListNode*>& lists)
{
//优先级队列默认大根堆,写一个仿函数
priority_queue<ListNode*, vector<ListNode*>, cmp> heap;
//头节点进小根堆
for(auto l : lists)
{
if(l) heap.push(l);
}
//合并
ListNode* ret = new ListNode(0);
ListNode* prev = ret;
while(!heap.empty())
{
ListNode* t = heap.top();
heap.pop();
prev->next = t;
prev = t;
if(t->next) heap.push(t->next);
}
prev = ret->next;
delete ret;
return prev;
}
};
分治
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* mergeKLists(vector<ListNode*>& lists)
{
return merge(lists,0,lists.size()-1);
}
ListNode* merge(vector<ListNode*>& lists, int left, int right)
{
if(left > right) return nullptr;
if(left == right) return lists[left];
int mid = (left+right) >> 1;
ListNode* l1 = merge(lists,left,mid);
ListNode* l2 = merge(lists,mid+1,right);
return mergeTwoList(l1,l2);
}
ListNode* mergeTwoList(ListNode* l1, ListNode* l2)
{
if(l1 == nullptr) return l2;
if(l2 == nullptr) return l1;
//合并链表
ListNode head;
ListNode* cur1 = l1, *cur2 = l2, *prev = &head;
head.next = nullptr;
while(cur1 && cur2)
{
if(cur1->val <= cur2->val)
{
prev->next = cur1;
prev = prev->next;
cur1 = cur1->next;
}
else
{
prev->next = cur2;
prev = prev->next;
cur2 = cur2->next;
}
}
if(cur1) prev->next = cur1;
if(cur2) prev->next = cur2;
return head.next;
}
};
运行结果:
25. K 个一组翻转链表
题目
题目链接:25. K 个一组翻转链表
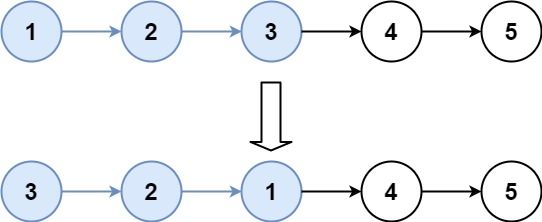
给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。
k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
示例 1:
输入:head = [1,2,3,4,5], k = 2
输出:[2,1,4,3,5]
示例 2:
输入:head = [1,2,3,4,5], k = 3
输出:[3,2,1,4,5]
提示:
- 链表中的节点数目为
n 1 <= k <= n <= 50000 <= Node.val <= 1000
**进阶:**你可以设计一个只用 O(1) 额外内存空间的算法解决此问题吗?
算法原理
这里还是模拟,分为两步走:
- 求出要逆序多少组,
group = n/k - 重复
group次逆置操作(头插)
代码实现
模拟:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k)
{
int n = 0;
ListNode* cur = head;
while(cur)
{
n++;
cur = cur->next;
}
int group = n/k;
ListNode* newHead = new ListNode(0);
ListNode* prev = newHead;
cur = head;
while(group--)
{
//记录要头插的位置
ListNode* tmp = cur;
for(int i=0; i<k; i++)
{
ListNode* next = cur->next;
cur->next = prev->next;
prev->next = cur;
cur = next;
}
prev = tmp;
}
//接上不需要翻转的节点
prev->next = cur;
cur = newHead->next;
delete newHead;
return cur;
}
};
运行结果: