线性表——(3)线性表的链式存储及其运算的实现

一、前言：

        由于顺序表的存储特点是用物理上的相邻关系实现逻辑上的相邻关系，它要求用连续的存储单元顺序存储线性表中各数据元素，因此，在对顺序表进行插入、删除时，需要通过移动数据元素来实现，这影响了运行效率。本节介绍线性表的链式存储结构，它不需要用地址连续的存储单元来实现，因为它不要求逻辑上相邻的两个数据元素在物理上也相邻。在链式存储结构中，数据元素之间的逻辑关系是通过“链”来连接的，因此对线性表的插入、删除不需要移动数据元素。

二、单链表： 

        链表是通过一组任意的存储单元来存储线性表中的数据元素的，那么怎样表示数据元素之间的线性关系呢?即如何来“链”接数据元素间的逻辑关系呢?为此，在存储数据元素时，对于每个数据元素ai，除了存放数据元素的自身信息 ai，还需要和 ai一起存放其后继数据元素 ai+1 所在的存储单元的地址，这两部分信息组成一个节点，节点的结构如图 A所示，每个数据元素皆是如此。存放数据元素自身信息的单元称为数据域，存放其后继数据元素地址的单元称为指针域。因此n个数据元素的线性表通过每个节点的指针域拉成了一个“链子”,称为链表。图A 所示链表的每个节点中只有一个指向后继的指针，所以称其为单链表。

图A  单链表节点的结构

链表是由节点构成的，节点定义如下: 

typedef struct LNode{
	datatype data;//存放数据元素 
	struct LNode *next;//存放下一个节点的地址 
}LNode,*LinkList;

定义头指针变量：

LinkList h;//定义头指针变量

图B 所示为线性表 (a1, a2, a3, a4, a5, a6, a7, a8)对应的链式存储结构示意图。 

图B 链式存储结构示意图

图C 链表示意图

 

        当然，必须将第一个节点的地址 160 放到一个指针变量中，如H;最后一个节点没有后继，其指针域必须置空(即NULL)，表明此表到此结束。这样就可以从第一个节点的地址开始“顺藤摸瓜”，找到表中的每个节点。
        作为线性表的一种存储结构，人们关心的是节点间的逻辑结构,而并不关心每个节点的实际地址,所以通常的单链表用如图C所示的形式表示而不用如图B 所示的形式表示，其中，符号“^”表示空指针(下同)。
        实际应用中通常用头指针来标识一个单链表，如单链表 L、单链表 H 等，是指某链表的第一 个节点的地址放在指针变量 L、H 中，头指针为“NULL”则表示一个空表。

        需要进一步指出的是: 上面定义的 LNode 是节点的类型，LinkList 是指向 LNode 类型节点的指针类型。为了增强程序的可读性，通常将标识一个链表的头指针定义为 LinkList 类型指针的变量，如LinkList L。当L有定义时，其值要么为 NULL(表示一个空表)，要么为第一个节点的地址，即链表的头指针。将运算中用到指向某节点的指针变量说明为: LNode *类型，如 

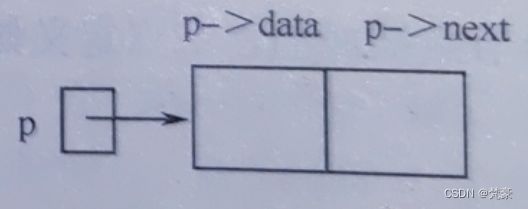
LinkList *p;

        则语句“p=malloc(sizeof(LNode));”完成了申请一块 LNode 类型的存储单元的运算，并将其地址赋值给指针变量 p。如图D所示，指针变量 p 所指的节点为*p，*p 的类型为 LNode 型，所以该节点的数据域为(*p).data 或 p->data，指针域为(*p).next 或 p->next，而语句“free(p);”则表示释放指针变量p所指的节点。 

图D 申请一个节点

三、单链表基本运算的实现： 

 建立单链表：

 ❤️在链表的头部插入节点建立单链表：

        链表与顺序表不同，它是一种动态管理的存储结构，链表中的每个节点占用的存储空间不是预先分配的，而是运行时系统根据需求生成的。因此，建立单链表要从空表开始，每读入一个数据元素则申请一个节点，然后插在链表的头部，图E展现了线性表(25,45,18,76,29)的链表建立过程，因为是在链表的头部插入，所以读入数据的顺序和线性表中的逻辑顺序是相反的。

图E  在链表头部插入节点建立单链表

⭐单链表的建立算法(头部插入)。 

LinkList Creat_LinkList1(){
	LinkList L=NULL;//空表L为表头
	LNode *s;
	int x;			//设数据元素的类型为int型 
	scanf("%d",&x);
	while(x!=flag){//设flag为数据元素输入结束的标志 
		s=malloc(sizeof(LNode));//为插入数据元素申请空间 
		s->next=L;			//将插入数据元素置入申请到的单元中 
		L=s;
		scanf("%d",&x); 
	} 
	return L;
}  

 ❤️在单链表的尾部插入节点建立单链表：

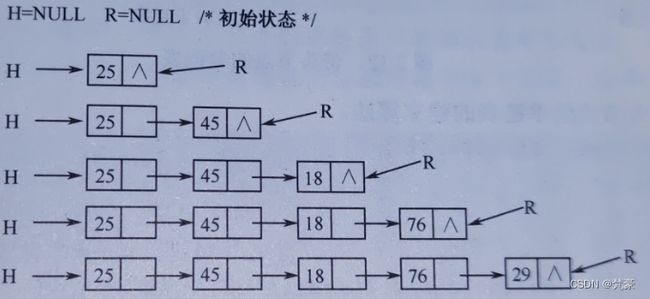
        头部插入建立单链表虽然简单，但读入的数据元素的顺序与生成的链表中数据元素的顺序是相反的。若希望次序一致，则用尾部插入的方法。因为每次运算都是将新节点插入到链表的尾部，所以需加入一个指针 R 用来始终指向链表中的尾节点。图 F展现了在表尾部插入节点建立链表的过程。 

图F  在链表尾部插入节点建立单链表

 

         算法思路:初始状态时，头指针 H=NULL，尾指针 R=NULL，按线性表中数据元素的顺序依次读入数据元素，不是结束标志时，申请节点，将新节点插入到R 所指节点的后面，然后R指向新节点。

⭐单链表的建立算法(尾部插入)。

LinkList Creat_LinkList2(){
	LinkList *s,*R=NULL;
	int x;//设数据元素的类型为int型
	scanf("%d",&x);
	while(x!=flag){
		s=malloc(sizeof(LNode));s->data=x;//申请空间并将插入数据元素置入该单元 
		if(L==NULL){
			L=s;//第一个节点的处理 
		} 
		else{
			R->next=s;//其他节点的处理 
		} 
		R=s;//R重新指向新的尾节点 
		scanf("%d",&x); 
	} 
	if(R!=RULL){
		R->next=NULL;//对于非空表，将尾节点的next指针置空 
	} 
	return L; 
}

 ❤️在带头节点单链表的表尾插入数据元素建立单链表：

        在上面的算法中，第一个节点的处理和其他节点是不同的，原因是第一个节点加入时链表为空，它没有直接前趋节点，它的地址就是整个链表的指针，需要放在链表的头指针变量中;而其他节点有直接前趋节点，其地址放入直接前趋节点的指针域。第一个节点的问题在很多运算中都会遇到，如在链表中插入节点时，将节点插在第一个节点位置和其他节点位置是不同的，在链表中删除节点时，删除第一个节点和其他节点的处理也是不同的。
        为了方便运算，有时在链表的头部加入一个头节点，头节点的类型与数据节点一致，标识链表的头指针变量L中存放该节点的地址，这样即使是空表，头指针变量L也不为空了。头节点的加入使得第一个节点的问题不再存在，也使得空表和非空表的处理一致。
        头节点的加入完全是为了运算的方便，它的数据域无定义，指针域中存放的是第一个数据节点的地址，当空表时该指针域为空。

        图G 和图H 分别是带头节点的单链表空表和非空表的示意图。                           

 

图G  空表

图H  非空表