【数据结构实验】排序（二）希尔排序算法的详细介绍与性能分析

1. 引言

  排序算法在计算机科学中扮演着至关重要的角色，对于数据的组织和搜索等任务有着深远的影响。希尔排序是一种插入排序的改进版本，通过引入增量的概念，能够在某些情况下显著提高排序的效率。

  本文将详细介绍希尔排序算法的原理、实现，以及对其性能进行分析。

2. 希尔排序算法原理

  希尔排序是一种基于插入排序的改进算法，由Donald L. Shell于1959年提出。其核心思想是将待排序的记录按下标的一定增量分组，对每组使用直接插入排序方法，随着增量逐渐减小，每组包含的记录越来越多，直至增量为1时，整个序列恰好被分成一个组，排序完成。

2.1 示例说明

  考虑一个包含16个记录的输入文件，取渐减增量序列为$8,4,2,1$。初始时，将输入文件分成8个组：

• 组1: $R_1,R_9$
• 组2: $R_2,R_{10}$
• 组3: $R_3,R_{11}$
• …
• 组8: $R_8,R_{16}$

  对每个组使用直接插入排序算法进行排序。然后，取增量值为4，将文件分成4个组：

• 组1: $R_1,R_5,R_9,R_{13}$
• 组2: $R_2,R_6,R_{10},R_{14}$
• 组3: $R_3,R_7,R_{11},R_{15}$
• 组4: $R_4,R_8,R_{12},R_{16}$

  再次对每个组使用直接插入排序。重复这个过程，取增量值为2和1，最终完成整个排序。

2.2 时间复杂性分析

  希尔排序的性能与所选取的分组长度序列密切相关。最坏情况下的时间复杂度为$O(n^2)$，但不同的分组长度序列会影响算法的实际性能。

• 当分组长度序列取$\frac{n}{2^i}$时，最坏情况下时间复杂度为$O(n^2)$。
• 实际应用中，取2.2作为递减因子效果更好。
• 当分组长度序列取形如$2^p{3}^q$且小于n的所有正整数的集合时，希尔排序的时间复杂度为$O(n\cdot ({\log }_{2}n{)}^2)$。

  1969年，V. Pratt证明了以上结论。目前已知的最好分组长度序列是$\{1,4,10,23,57,132,301,701,1750,...\}$，具有此分组序列的希尔排序比插入排序和堆排序要快。在小数组情况下比快速排序快，但对于大数组则可能比快速排序慢。此外，希尔排序是不稳定的排序算法。

3. 实验内容

3.1 实验题目

以{7，5，3，1}为渐减增量序列实现希尔排序算法 ShellSort.

（一）输入要求

第一组输入数据：
{27，32，33，21，57，96，64，87，14，43，15，62，99，11}
第二组输入数据：
{11，14，15，21，27，32，33，43，57，62，64，87，96，99}
第三组输入数据：
{99，96，87，64，62，57，43，33，32，27，21，15，14，11}

（二）输出要求

对每组输入数据，输出以下信息（要求必须要有关于输出数据的明确的提示信息）:

1. 输出整个排序过程总的关键词比较次数和总的记录移动次数；
2. 每发生一次记录插入，输出整个文件一次；
3. 输出增量为 7、5、3、1 时的关键词比较次数和记录移动次数

3.2 算法实现

#include 
#define n 14
void ShellSort(int R[n]){
    int r,i,j,k,Compare=0,Move=0;
    int d=7;	//初始化增量值为7
    while(d>0){		//不断分组，并对各组排序
   		int compare=0,move=0;
        for(i=d;i<n;i++){	//对各组做直接插入排序
            r=R[i];
            j=i;
            while(j>d-1&&R[j-d]>r){
            	compare++;
                R[j]=R[j-d];
                j-=d;
            }
            if(j!=i){
            	move++;
            	R[j]=r;
            	for(k=0;k<n;k++){
           	 	    printf("%d ", R[k]);
            	}
            	printf("\n");
			}  
        }
        printf("\n增量值为%d时的关键词比较次数是%d，记录移动次数是%d\n\n",d,compare,move);
        d=d-2; 	//计算新的增量值,{7，5，3，1}
   		Compare+=compare;
		Move+=move;
    }
    printf("关键词的总比较次数是%d，总的记录移动次数是%d\n",Compare,Move);
}
int main(){
    int i;
    //int R[n]={27,32,33,21,57,96,64,87,14,43,15,62,99,11};
    int R[n]={11,14,15,21,27,32,33,43,57,62,64,87,96,99};
    //int R[n]={99,96,87,64,62,57,43,33,32,27,21,15,14,11};
    ShellSort(R);
    printf("最后结果：");
    for(i=0;i<n;i++){
        printf("%d ",R[i]);
    }
}

3.3 代码解析

• 宏定义

#define n 14

  定义宏 n，表示数组的长度为14，在后续代码中可以方便地使用 n 来表示数组的长度，而不需要硬编码。

• 希尔排序函数
    参数是一个整型数组 R，表示待排序的数组。在函数内部，通过不断缩小增量的方式，对数据进行插入排序。具体来说，在每一轮循环结束后，更新增量的值，采用一定的方式递减。这里选择减小2的增量序列 {7, 5, 3, 1}。

  int d = 7;
  while (d > 0) {
  	// ...
  	d=d-2; 	//计算新的增量值,{7，5，3，1}
  	// ...
  }
  

    使用 while 循环，不断缩小增量 d，并在每一轮循环中进行插入排序。增量的选择是关键，这里初始设置为7，然后逐渐减小。

  for (i = d; i < n; i++) {
  // ...
  }
  

  针对每个分组，从第 d 个元素开始，进行插入排序。

  while (j > d - 1 && R[j - d] > r) {
  // ...
  }
  

  在插入排序的过程中，通过比较和移动元素，确保分组内的元素是有序的。

• 输出结果

printf("\n增量值为%d时的关键词比较次数是%d，记录移动次数是%d\n\n", d, compare, move);

  在每一轮排序结束后，输出该轮排序的比较次数和记录移动次数，从而了解算法在不同步长下的性能。

printf("关键词的总比较次数是%d，总的记录移动次数是%d\n", Compare, Move);

  在整个排序完成后，输出总的比较次数和记录移动次数，提供了算法整体性能的信息。

• 主函数

int main(){
    int i;
    // int R[n]={27,32,33,21,57,96,64,87,14,43,15,62,99,11};
    // int R[n]={11,14,15,21,27,32,33,43,57,62,64,87,96,99};
    int R[n]={99,96,87,64,62,57,43,33,32,27,21,15,14,11};
    ShellSort(R);
    printf("最后结果：");
    for(i=0;i<n;i++){
        printf("%d ",R[i]);
    }
}

  创建一个包含14个元素的数组 R，并调用 ShellSort 函数对其进行排序。最后输出排序后的数组。

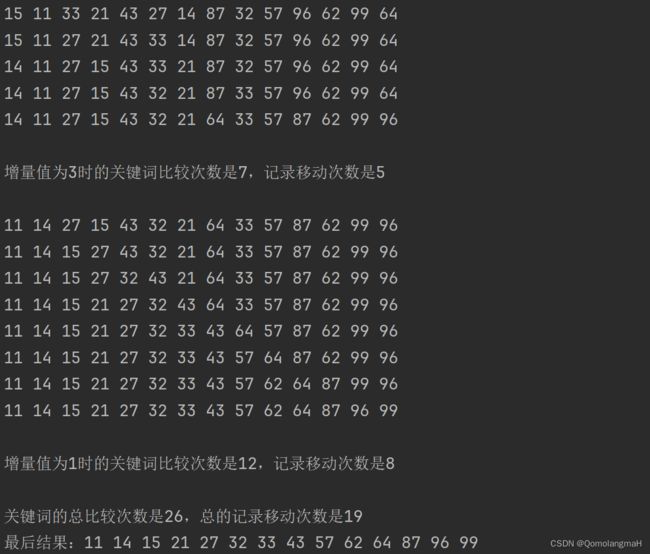
3.4 实验结果

4. 实验结论

  希尔排序是一种高效的排序算法，通过引入增量的方式，能够在某些情况下显著提高插入排序的性能。选择合适的分组长度序列对算法的实际效果有重要影响，而已知的最佳序列$\{1,4,10,23,57,132,301,701,1750,...\}$在实践中表现优异。

  需要注意的是，希尔排序是不稳定的排序算法。在实际应用中，根据数据规模和特性选择不同的排序算法是很重要的，希尔排序在一些场景下可能比其他排序算法更适用。希尔排序的性能对于分组长度序列的选择非常敏感，因此在实际使用中需要根据具体情况进行调优。